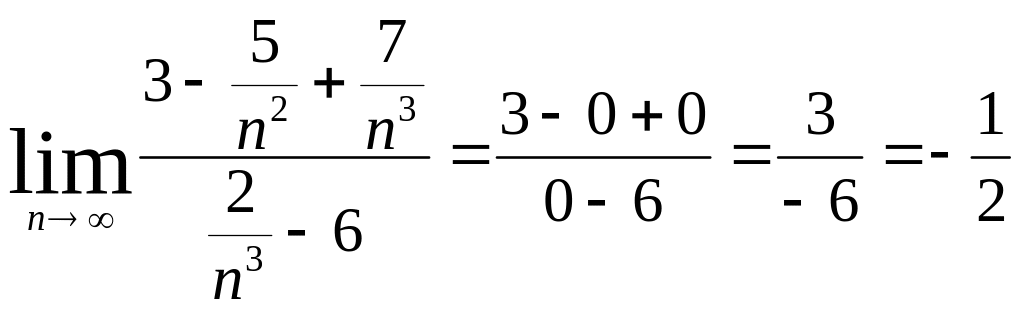- •Рабочая тетрадь по дисциплине «Математика» раздел «Элементы математического анализа»
- •Содержание
- •Введение
- •Тема: Понятие функции. Способы задания функции. Свойства функции.
- •1. Контрольные вопросы:
- •2. Дайте определения следующим понятиям:
- •3. Практические задания по теме:
- •4. Задания для самостоятельной работы
- •Тема: Числовая последовательность. Предел последовательности.
- •1. Контрольные вопросы:
- •2. Практические задания по теме:
- •3. Задания для самостоятельной работы
- •Тема: Предел функции
- •1. Контрольные вопросы:
- •2. Практические задания по теме:
- •3. Задания для самостоятельной работы
- •Тема: Непрерывность функции
- •2. Практические задания по теме:
- •3. Задания для самостоятельной работы
- •Тема: Производная функции в точке, её геометрический, механический и экономический смысл
- •2. Практические задания по теме
- •Тема: Производная функции, формулы и правила дифференцирования
- •2. Практические задания по теме:
- •Тема: Исследование функций и построение графиков
- •2. Практические задания по теме
- •3. Задания для самостоятельной работы
- •Тема: Дифференциал функции
- •1. Контрольные вопросы:
- •2. Практические задания по теме
- •Тема: Неопределенный интеграл
- •1. Контрольные вопросы:
- •2. Практические задания по теме:
- •Тема: Определенный интеграл
- •1. Контрольные вопросы:
- •2. Практические задания по теме
- •3. Задания для самостоятельной работы:
- •4. Задания для самостоятельной работы:
- •Тема: Функции нескольких переменных
- •1. Контрольные вопросы:
- •2. Практические задания по теме:
- •Расчетно-графические задания к разделу «Элементы математического анализа»
Тема: Числовая последовательность. Предел последовательности.
1. Контрольные вопросы:
1. Что называется числовой последовательностью?
______________________________________________________________________________________________________________________________________________________________________________________________________
2. Как найти члены последовательности, зная формулу общего члена?
____________________________________________________________________________________________________________________________________
3. Дайте определение предела последовательности:
______________________________________________________________________________________________________________________________________________________________________________________________________
4. Как
при нахождении предела последовательности
раскрывать неопределённости вида (![]() )
,
)
,
![]() ?
?
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Практические задания по теме:
1. Написать первые пять членов последовательности, и изобразить их на числовой прямой:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Зная первые члены последовательности, написать формулу её общего члена:
1,1/3,1/5,1/7,…. _____________________________________________________
1,1/4,1/9,1/16,1/25,….________________________________________________
![]() _________________________________________________
_________________________________________________
-1, 2, -3, 4,5….______________________________________________________
3. Доказать, что число является пределом последовательности, пользуясь определением:
При выполнении задания 3 можно пользоваться следующим алгоритмом:
Берём любое 0, составляем неравенство | хn-А |<, решаем это неравенство относительно n, в результате решения находим число, зависящее от , обозначим его за N, получим неравенство nN.
Рассмотрим
пример: Доказать, что
![]()
Берём
любое 0,
составляем неравенство
![]()
![]()
![]()
![]() .
Если =0,1,то
n
18/
.
Если =0,1,то
n
18/
1. ![]()
______________________________________________________________________________________________________________________________________________________________________________________________________
2. ![]() _____________________________________________________
_____________________________________________________
3. ![]()
4.Найти предел последовательности:
При
нахождении предела последовательности
могут встретиться следующие неопределённости
,
![]() .
Чтобы устранить неопределённость 1-ого
вида разделите числитель и знаменатель
дроби на степень с наивысшим показателем,
найти полученный предел.
.
Чтобы устранить неопределённость 1-ого
вида разделите числитель и знаменатель
дроби на степень с наивысшим показателем,
найти полученный предел.
№ |
Алгоритмы |
Выполнение соответствующего алгоритма |
1 |
Подставить предельное значение n в выражение |
|
2 |
Определить вид неопределённости |
|
3 |
Находим степень с наивысшим показателем |
n3 |
4 |
Делим числитель и знаменатель дроби на n3 |
|
Чтобы устранить неопределённость 2-ого вида надо умножить и разделить разность на сопряжённое выражение, выполнить преобразования и найти предел.
№ |
Алгоритмы |
Выполнение соответствующего алгоритма |
1 |
Подставить предельное значение n в выражение |
|
2 |
Определить вид неопределённости |
|
3 |
Умножаем и делим на сопряжённое выражение |
|
4 |
Найти предел полученного выражения |
|