Тема: Определенный интеграл
1. Контрольные вопросы:
1. Что называется интегральной суммой функции f(x) на отрезке a,b?
__________________________________________________________________
2. Что называется определенным интегралом функции f(x) на отрезке a,b?
__________________________________________________________________
3. В чем заключается геометрический смысл определенного интеграла?
__________________________________________________________________
4. Перечислите основные свойства определенного интеграла;
______________________________________________________________________________________________________________________________________________________________________________________________________
5. Запишите формулу Ньютона – Лейбница для вычисления определенного интеграла _________________________________________________________
2. Практические задания по теме
Задание1. Вычислить определенный интеграл:
1.1.
=_______________________________________________
________________________________________________________________
1.2.
=
Воспользуемся заменой переменной: пусть_______. Тогда
___________________________________. Найдем пределы интегрирования по переменной t; еслих=0,то _________ если х=ln2, то__________________
Искомый интеграл примет вид:
__________________________________________________________________
1.3.
Воспользуемся формулой интегрирования по частям:
пусть ______________________________________________________________________________________________________________________________________________________________________________________________________
3. Задания для самостоятельной работы:
1.
;
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
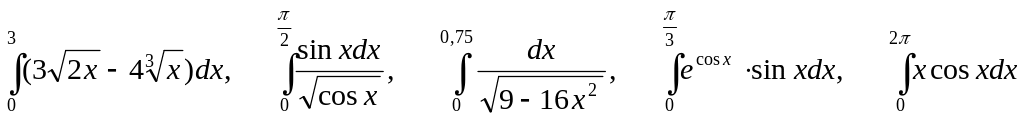2.
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
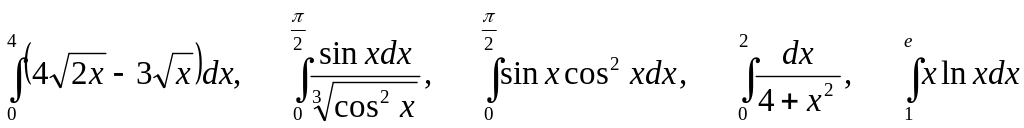
3.
;
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
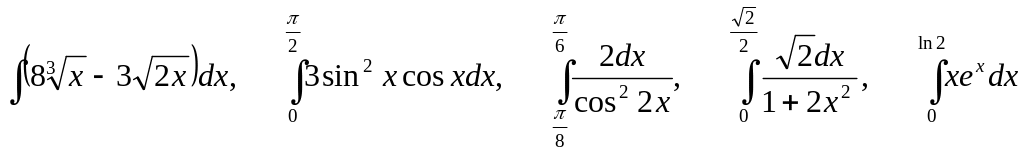Задание 2. Найти площадь фигуры, ограниченной линиями:
Рассмотрим пример: Найти площадь фигуры, ограниченной линиями
у=- х2+х+4 и у=-х+1
1. Выполним чертеж
2. Найдем точки пересечения линий у=- х2+х+4 и у=-х+1
__________________________________________________________________
3. По формуле площади фигуры получим:
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________