Билет №1

1. Найти по определению у (1) если у=

_{у(1) = –7}

2. Разложить по степеням х-3 функцию х 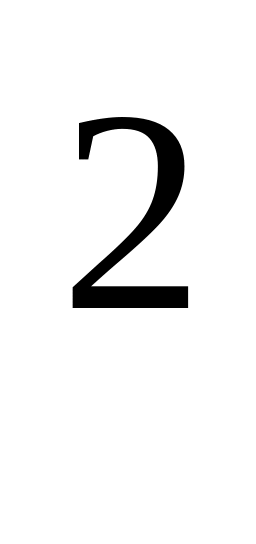+3х – 4

х +3х – 4 = (х – 3)² + 6х – 9 + 3х – 4 = (х – 3)² + 9(х – 3) +14

3. Найти градиент и матрицу Гессе для функции z= x -3xy+2y

Вычислим частные производные.

Запишем градиент функции

z = или другая форма записи gradz =

gradz =

Матрица Гессе:

4. Найти

Разложение на простые дроби

х² – 5х + 6 = 0

Д = 25 – 24 = 1 х₁ = 2, х₂ = 3.

х² – 5х + 6 = (х – 2)(х – 3)

Ах–3А + Вх –2В = 3х+ 5

А + В = 3 2А + 2В = 6

–3А –2В = 5 –3А – 2В = 5

 А = –11; В = 14.

5. Найти

Ответ:

6. Исследовать сходимость

1+2x+3x +4x +…

1+2x+3x +4x +…+ nx^n–1

Для нахождения интервала сходимости данного ряда применим признак Даламбера.

Ряд будет сходится, если

х< 1

–1<x<1. Следовательно, ряд сходится на интервале (–1; 1), R = 1.

Выясним вопрос о сходимости ряда на концах интервала.

При x = –1 ряд примет вид: = 1 – 2 + 3 – 4 + …

ряд расходится, точка x = –1 не принадлежит области сходимости.

При x = 1 ряд примет вид: = 1 + 2 + 3 + 4 + …

ряд расходится, точка x = 1 не принадлежит области сходимости.

(ряды расходятся, так как предел общего члена не равен нулю).

Ответ: (–1; 1)

7. Из 5 белых, 7 красных и 4 синих шариков выбрали 2. Какова вероятность того, что среди них будет хотя бы 1 синий?

Воспользуемся классической формулой для вычисления вероятности:

где m – число благоприятных событию А случаев;

n – число всех случаев.

Обозначим событие А – будет выбран хотя бы 1 синий шарик.

Рассмотрим противоположное событие – не вынут ни одни синий шарик, т.е. белые или красные.

Р(А) = 1 – Р( ) =

Ответ:

8. Закон распределения вероятностей

Х	-31	2.2	1	8
р	0.2	0.63	0.02	?

Найти р(8) и М(Х).

Найдем р(8)

0,2 + 0,63 + 0,02 + р = 1

р + 0,85 = 1

р(8) = 0,15

М(х) = –310,2 + 2,20,63 + 10,02 + 10,02 = –6,2 + 1,386 + 0,02 + 1,2 = –3,594

9.Теорема Ролля.

Пусть функция f: [a, b] → R непрерывна на сегменте [a, b], и имеет конечную или бесконечную производную внутри этого сегмента. Пусть, кроме того, f(a) = f(b). Тогда внутри сегмента [a, b] найдется точка ξ такая, что f'(ξ) = 0.

10. Найти общее решение

y + 4y + 5y =e (3x – 1)

Решение.

Общее решение неоднородного линейного уравнения с постоянными коэффициентами равно сумме соответствующего однородного уравнения и частного решения исходного однородного уравнения: y_неодн =y_одн + у_част

Найдем решение однородного уравнения

y + 4y + 5y= 0

Составляем характеристическое уравнение и определяем его корни

²+ 4+5= 0

найдем его корни

Д=16 – 20 = –4; ₁= –2 i– два комплексных корня, поэтому общее решение имеет вид:

y_одн =e^–2x(C₁cosх + C₂sinх)

где С₁ и С₂– произвольные постоянные.

Найдем частное решение уравнения.

у_част.=(Ax + В)e^2x

у_част =2(Ax + В)e^2x + Ae^2x= (2Ax+ А+ 2В)e^2x

у_част.= 2(2Ax+ А+ 2В)e^2x + 2Ae^2x= (4Аx + 4А +4)e^2x

Подставляем функцииу_част,у_част и у_част.в исходное уравнение

(4Ax + 4A + 4В)e^2x + 4(2Ax + A + 2В)e^2x + 5(Ax + В)e^2x= (3х– 1)e^2x

4Ax + 4A + 4В + 8Ax + 4A + 8В + 5Ax + 5В = 3х – 1

17Ax+8A+ 17В= 3x– 1

Тогда искомое частное решение

у_част.=

Итак, общее решение исходного уравнения

y = e^–2x(C₁cosх + C₂sinх)+

Ответ: y = e^–2x(C₁cosх + C₂sinх)+

11. Решить задачу Коши

Решение.

Уравнение с разделяющимися переменными.

Подставим начальное условие

Ответ:

Билет №2

1. Найти по определению у (2), если у =

у(2) =

2. Разложить по степеням х+2функцию х – 7х+1

х – 7х+1 = (х + 2)² – 4х – 4 – 7х + 1 = (х + 2)² – 11(х + 2) + 19

3. Найти градиент и матрицу Гессе для функции z= x +7x y-y

Вычислим частные производные.

Запишем градиент функции

z = или другая форма записи gradz =

gradz =

Матрица Гессе:

4. Найти

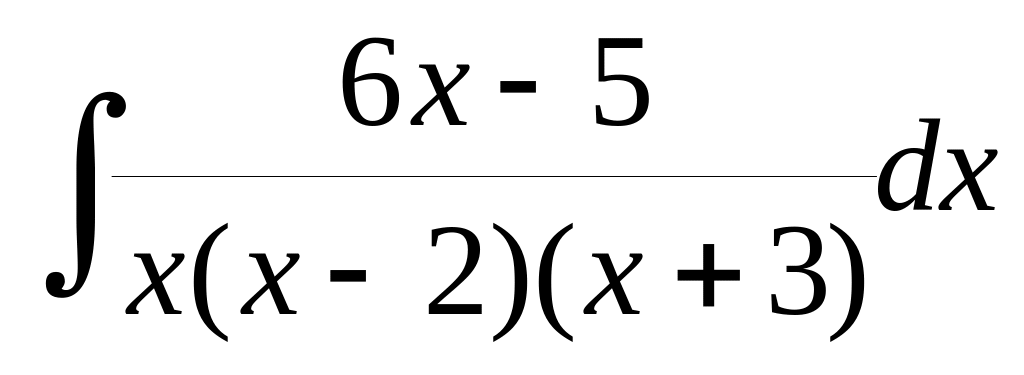
Разложение на простые дроби

А(х – 2)(х + 3)+ Вх(х + 3) + Сх(х – 2) = 6х – 5

Ах² + Ах– 6А + Вх² + 3Вх + Сх² – 2Сх= 6х– 5

х²: А + В+ С= 0

х¹: А+3В– 2С= 6

х⁰: –6А = –5 А = ;

В = ; С = ;

5. Найти

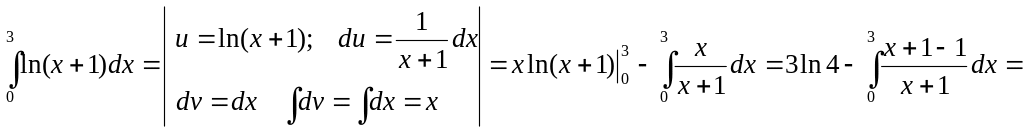
6. Исследовать сходимость

2x+4x +6x +8x …

2x+4x +6x +8x +…+ 2nx^2n–1

Для нахождения интервала сходимости данного ряда применим признак Даламбера.

Ряд будет сходится, если

х²< 1

–1<x<1. Следовательно, ряд сходится на интервале (–1; 1), R = 1.

Выясним вопрос о сходимости ряда на концах интервала.

При x = –1 ряд примет вид: = –2 + 4 – 6 + …

ряд расходится, точка x = –1 не принадлежит области сходимости.

При x = 1 ряд примет вид: = 2+4 + 6+8 + …

ряд расходится, точка x = 1 не принадлежит области сходимости.

(ряды расходятся, так как предел общего члена не равен нулю).

Ответ: (–1; 1)

7. Вероятность поймать большую и хитрую рыбу при одном забросе блесны равна 0,4. Какова вероятность при 4 забросах блесны поймать 2 рыбы?

Формула Бернулли

n= 4k= 2 p=0,4q= 0,6

8. Закон распределения вероятностей

Х	4,5	2	-5	10
Р	?	0.3	0.35	0,25

Найти р(4,5) и М(Х).

Найдем р(4,5)

р + 0,3 + 0,35 + 0,25 = 1

р + 0,9 = 1

р(4,5) = 0,1

М(х) = 4,50,1 + 20,3 – 50,35 + 100,25 = 0,45 + 0,6 – 1,75 + 2,5 = 1,8

9. Теорема Лагранжа.

Если функция f: [a, b] → R непрерывна на сегменте [a, b] и имеет конечную или бесконечную производную во внутренних точках этого сегмента, то  (a; b) такое, что f(b) –f(a) = f'(ξ)(b–a).

10. Найти общее решение

y – 5y + 6y=(x – 3)e

Решение.

y_неодн =y_одн + у_част

Найдем решение однородного уравнения

y – 5y + 6y= 0

Составляем характеристическое уравнение и определяем его корни

²–5+ 6 = 0

найдем его корни

Д= 25 – 24 = 1; ₁= 2;₂= 3 – действительные и различные, поэтому общее решение имеет вид:

y = C₁e^2x + C₂e^3x,

где С₁ и С₂– произвольные постоянные.

₁= 2 – кратный корень.

Найдем частное решение уравнения.

у_част.= (Ax + В)xe^2x

у_част =2(Ax² + Вx)e^2x + (2Ax + В)e^2x= (2Ax² + 2Ax + 2Вx + В)e^2x

у_част.=2(2Ax² +2Ax + 2Вx +В)e^2x + (4Ax + 2A + 2В)e^2x= (4Ax² + 8Ax + 4Вx + 2A + 4В)e^2x

Подставляем функцииу_част,у_част и у_част.в исходное уравнение

(4Ax² + 8Ax + 4Вx + 2A + 4В)e^2x–5(2Ax² + 2Ax + 2Вx + В)e^2x + 6(Ax² + Вx)e^2x = (x– 3)e^2x

4Ax² + 8Ax + 4Вx + 2A + 4В – 10Ax²–10Ax–10Вx– 5В + 6Ax²+ 6Вx= x– 3

–2Ax+2A–В= x– 3

Тогда искомое частное решение

у_част.=

Итак, общее решение исходного уравнения

y = C₁e^2x + C₂e^3x

Ответ: y = C₁e^2x + C₂e^3x

11. Решить задачу Коши

Решение.

Уравнение с разделяющимися переменными.

Подставим начальное условие

Ответ:

Билет №3

1. Найти по определению у (-3) если у = .

у(–3) =

2. Разложить по степеням х+5 функцию х +5х+11.

х + 5х+ 11 = (х + 5)² – 10х – 25 + 5х + 11 = (х + 5)² – 5(х + 5) + 11

3. Найти градиент и матрицу Гессе для функции z= x -4x y-y х

Вычислим частные производные.

Запишем градиент функции

z = или другая форма записи gradz =

gradz =

Матрица Гессе:

4. Найти

Разложение на простые дроби

А(х + 1)(х – 4) + В(х – 2)(х – 4) + С(х–2)(х + 1) = 2х + 5

Ах² – 3Ах– 4А + Вх² – 6Вх + 8В + Сх² – Сх – 2С= 2х + 5

х²: А + В + С = 0 А = –В – С

х¹: –3А – 6В – С = 2 С = –2 – 3А – 6В = –2 + 3В + 3С– 6В = – 2 – 3В + 3С

х⁰: –4А + 8В – 2С = 5 2С = 2 + 3В; С = 1 + 1,5В

А = –В – С = –В– 1 – 1,5В = –1 – 2,5В

4 + 10В + 8В – 2 – 3В = 5

15В = 7 В = 0,2; А = –1,5; С = 1,3.