ЛЕКЦИИ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ.

Лекция 1

Введение

В основу курса положены две дисциплины, начертательная геометрия и инженерная графика.

Начертательная геометрия относится к разряду прикладных математических наук. Она дает общий метод решения стереометрических задач геометрическими построениями на плоскости. Первый труд по на­чертательной геометрии был опубликован в 1799 году французским ученым Гаспаром Монжем. Большой вклад в эту науку внесли наши русские ученые Севостьянов, Макаров, Курдюмов, Федоров и др.

Черчение – это язык техники. Чертежом называется изображение предмета, построенное по законам начертательной геометрии и в соответ­ствии с правилами, установленными государственными стандартами.

Методы проецирования

Под пространственным объектом подразумевается часть простран­ства, занятая реально существующим объектом (предмет, фигура). Эта часть пространства имеет метрическую характеристику (длина, ширина, высота).

Пространственный объект может быть нуль мерным – точка, одно­мерным – линия, двумерным – плоскость, трехмерным – объемная фигура. В этом курсе рассматривается только Евклидово пространство.

Как всякая наука, начертательная геометрия имеет свою символику. Точки обозначаются прописными буквами латинского алфавита, а плоско­сти – прописными буквами греческого алфавита.

1. Центральное проецирование

Проецирование объекта из данного центра называется центральным или коническим. Полученные проекции называются перспективными и применяются, в основном, в строительстве и архитектуре.

2. Параллельное проецирование

Проецирование предмета из бесконечно удаленного центра называ­ется параллельным или цилиндрическим.

Некоторые свойства проецирования

1. Проекция точки на плоскость есть точка А

2. Проекция прямой линии на плоскости есть прямая. Если прямая совпадает с проецирующим лучом, то ее проекцией является точка.

3. Если точка принадлежит линии, то проекция точки принадлежит проекции линии.

4. Каждая точка и линия в пространстве имеют единственную свою проекцию.

5. Каждая точка на плоскости может быть проекцией множества точек, если через них проходит общая для них проецирующая прямая.

6. Из этого свойства следует, что одна проекция объекта не определяет его положения в пространстве.

Комплексный чертеж в ортогональных проекциях. Точка

Поверхность каждого предмета образуется из геометрических эле­ментов – точек, прямых и кривых линий, плоскостей и кривых поверхно­стей.

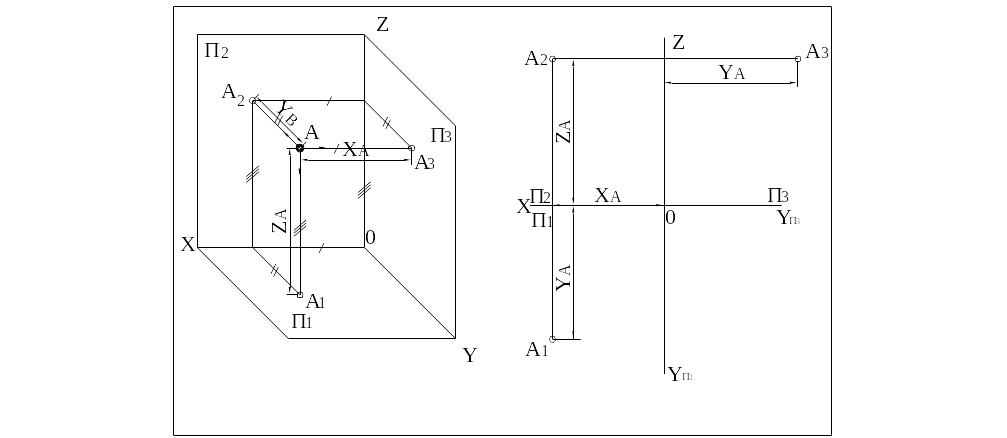
Для получения изображения предметов их проецируют на взаимно перпендикулярные (ортогональные) плоскости проекций. Спроецируем точку А на горизонтальную плоскость проекций П₁, фронтальную П₂, и профильную П₃. Проекции точки обозначим соответственно: горизонтальную – А₁, фронтальную – А₂ профильную – А₃. Линии пересечения плоскостей проекций служат осями координат – П₁ / П₂ – x; П₂ / П₃ – z; П₁ / П₃ – y. Расстояния от точки А до плоскостей проекций представляют собой координаты точки А (X_А, Y_А, Z_А). Координатами точки называют число, выражающее расстояние от точки до соответствующей плоскости проекций. Точка пространства определяется тремя координатами - А(x, y, z)

Выводы:

1. если точка находится в пространстве, то ни одна из ее координат не равна 0;

2. если одна координата равна 0, то точка находится на плоскости;

3. если - 2 – то на оси;

4. если - 3 – то в начале координат.

Развернув плоскости проекций до совмещения с плоскостью П₂, получим комплексный чертеж в ортогональных проекциях. Очертания плоскостей проекций показывать нет необходимости. Линии, соответствующие координатам Y_А + Z_А и координатам X_А + Y_А, образуют линии проекционной связи, перпендикулярные соответствующим осям.

Любые две проекции точки однозначно определяют положение точки относительно трех плоскостей проекций, так как содержат все три координаты.

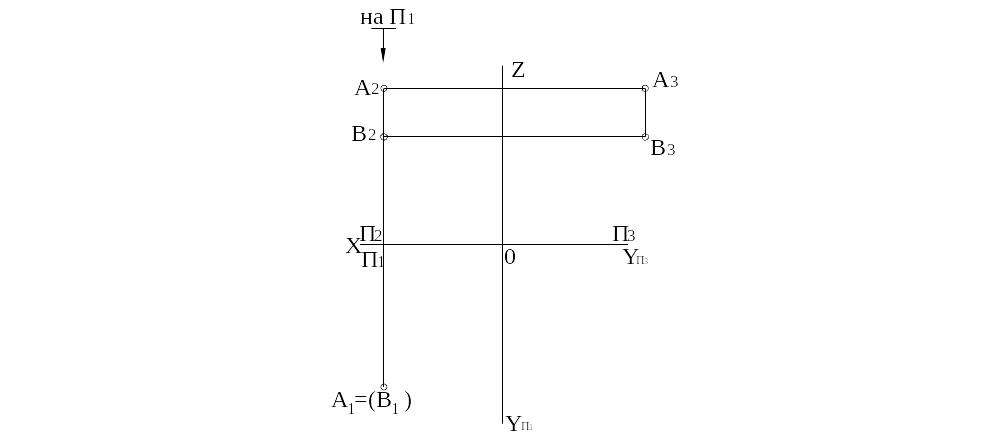
Точки, лежащие на одном проецирующем луче к какой либо плоскости проекций, называются конкурирующими.

Пример эпюра горизонтально-конкурирующих точек А и В приведен ниже.

В идимость точек на горизонтальной плоскости определяет направление взгляда, выраженного символом

Лекция 2