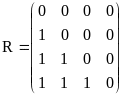3. Всюду определенность

Соответствие называется всюду определенным, если его область определения совпадает со всем множеством , т.е. .

Соответствия из примеров 1, 2, 3 не являются всюду определенными.

• Пример 4. На множествах и задано соответствие 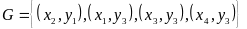(рис.6). Это соответствие всюду определенное, а также функциональное, но не инъективное.

4. Сюръективность

Соответствие называется сюръективным, если его область значений совпадает со всем множеством , т.е. . Соответствие из примера 1 сюръективно, так как . Соответствия из примеров 2, 3, 4 не сюръективны.

• Пример 5. На множествах и задано соответствие (рис.7). Это соответствие сюръективно и функционально, но не инъективно и не всюду определено.

5. Биективность

Соответствие называется биективным, если оно одновременно функционально, инъективно, всюду определено и сюръективно. Соответствия из примеров 1- 5 не биективны.

• 

  

  

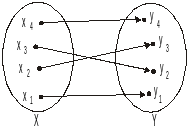
  Пример 6. На множествах и задано соответствие 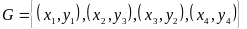(рис.8). Это соответствие биективно.

Рис.6 Рис.7 Рис.8

Рис.9. Свойства соответствий

Виды соответствий

Функцией из в называется всюду определенное функциональное соответствие между числовыми множествами. Обозначается или .

Если Х – множество функций, то f – функционал (определенный интеграл).

Если Х и Y – множествf функций, то f – оператор (производная).

4. Кардинальные числа

Два множества называются равномощными, если между элементами этих множеств можно установить взаимно-однозначное соответствие.

Очевидно, что между двумя конечными множествами можно установить взаимно-однозначное соответствие тогда и только тогда, когда оба множества содержат одинаковое количество элементов.

Такое соответствие можно установить и между некоторыми бесконечными множествами. Например, если каждому натуральному числу n поставить в соответствие число 2 n, то получится взаимно-однозначное соответствие между множеством всех натуральных чисел и множеством четных чисел. Отсюда следует, что эти два множества равномощны несмотря на то, что множество четных чисел является частью (подмножеством) множества натуральных чисел.

В теории множеств не всегда верно то, что часть меньше целого. Ценность понятия мощности, особенно в приложении к бесконечным множествам, состоит в том, что существуют неравные бесконечные множества, т.е. речь может идти о том, что одна бесконечность больше (или меньше) другой бесконечности. Например, мощность булеана бесконечного множества М больше мощности самого множества М, .

Множество, равномощное множеству натуральных чисел, называется счетным множеством, т.е. элементы счетного множества можно пронумеровать натуральными числами.

Кардинальное число – класс равномощных множеств.

5. Отношение как частный случай соответствия

Отношение - соответствие, заданное на одном и том же множестве .

Между элементами этого множества могут существовать определенные логические связи, или, иначе говоря, элементы находятся в определенных отношениях друг с другом.

Тот факт, что элемент находится в отношении с элементом записывается так или , читается « находится в отношении с ».

Отношение между двумя элементами называется бинарным, между тремя - тернарным и т.д., отношение между n элементами называется n-арным (эн-арным).

Тому таблицю множення чисел, скажімо, від 1 до 4 може бути подано як тернарне відношення на множині Х = {х|(х  Z)(х  1) (х  16)}, але замість рядків

1  1 = 1 2  1 = 2 3  1 = 3 4  1 = 4

1  2 = 2 2  2 = 4 3  2 = 6 4  2 = 8

1  3 = 3 2  3 = 6 3  3 = 9 4  3 =12

1  4 = 4 2  4 = 8 3  4 = 12 4  4 = 16

маємо Г  Хⁿ, де Г = {(1, 1, 1), (1, 2, 2), (1, 3, 3), (1, 4, 4), (2, 1, 2), (2, 2, 4), (2, 3, 6), (2, 4, 8), (3, 1, 3), (3, 2_, 6), (3, 3, 9), (3, 4, 12), (4, 1, 4), (4, 2, 8), (4, 3, 12), (4, 4, 16)}.

Властивості відношень та операції над відношеннями вівчає алгебра відношень або реляційна алгебра. Реляційна алгебра послуговує теоретич­ною основою для побудови реляційних баз даних, широковживаних ком­п'ютерних інформаційних технологій. Зберігання табличної інформації у вигляді множин кортежів дає можливість економити пам'ять комп'ютера, а операції пошуку та оновлення інформації часто зведені до теоретико-множинних операцій над множинами кортежів.

Мы будем рассматривать только бинарные отношения. Эквивалентом понятия отношения могут быть выражения «быть равным», «быть меньше (больше)», «быть братом», «быть жителем одного и того же города» и т.д.

Способы задания отношений

Отношения задаются также как и соответствия: перечислением пар элементов, входящих в соответствие, таблицей (матрицей) и графом.

Пример 1. На множестве задано отношение - «быть больше». Представить его различными способами.

Перечислением данное отношение представляется в виде

В виде таблицы отношение выглядит так

2-я к. 1-я к.	1	5	6	30
1	0	0	0	0
5	1	0	0	0
6	1	1	0	0
30	1	1	1	0

Поскольку отношение задается на одном и том же множестве, то в таблице отмечено, где расположены первые и вторые координаты отношения. Ниже данное отношение представлено матрицей и графом