14

Дискретка – ХАИ. Тема 2. Соответствия и отношения

Соответствия и отношения

План

1. Определение соответствия.

2. Операции над соответствиями.

3. Свойства соответствий.

4. Кардинальные числа.

5. Отношение как частный случай соответствия.

6. Операции над отношениями.

7. Свойства отношений.

8. Виды отношений.

1. Определение соответствия

Соответствием называется какая-либо связь между элементами одного множества или элементами разных множеств.

Понятие соответствия - это наиболее общее понятие, лежащее в основе таких понятий как функция, отображение и др.

Чтобы задать соответствие между элементами множеств и необходимо указать, какие элементы соответствуют элементам , т.е. указать пары . Декартово произведение – универсам соответствия.

• Пример 1. Пусть между элементами множеств 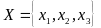и 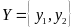задано соответствие 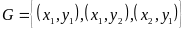.. 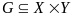, и может полностью совпадать с ним в частных случаях.

Областью определения соответствия является множество его первых координат . Областью определения соответствия, приведенного в примере 1 является множество . Область определения соответствия часто называют множеством прообразов.

Областью значений соответствия является множество его вторых координат . Областью значений соответствия, приведенного в примере 1 является множество . Область значений соответствия часто называют множеством образов.

Способы задания соответствий

1. Перечисление всех элементов (пар) соответствия . Соответствие в примере 1 задано именно этим способом.

2. Табличный или матричный способ.

Y X	y1	y2
x1	1	1
x2	1	0
x3	0	0

Первая строка таблицы содержит все элементы множества Y, а первый столбец этой таблицы содержит все элементы множества X. Если в соответствие входит пара , то на пересечении строки, соответствующей , и столбца, соответствующего , ставится 1. Таким образом, пары, входящие в соответствие, отмечаются в таблице 1, остальные клетки таблицы заполняются нулями. Данная таблица задает соответствие из примера 1.

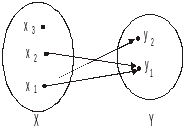
3. Графический способ. Соответствие задается графом (граф - это множество точек, называемых вершинами, и множество линий, называемых ребрами или дугами). Каждому элементу множества, на котором задано соответствие соответствует вершина графа. Если элементу x₁ соответствует элемент y₁, то из вершины x₁ в вершину y₁ проводится стрелка (дуга графа) (рис.2).

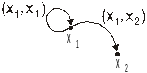
Если элемент x₁ поставлен в соответствие самому себе, т.е. в соответствии имеется пара , то ребро графа начинается и заканчивается в вершине x₁ (рис.3). Такое ребро называется петлей.

Рис.2 Рис.3

2. Операции над соответствиями

Поскольку соответствия являются множествами, то над ними возможны все те операции, которые выполняются над множествами: объединение, пересечение, разность, симметрическая разность, дополнение (до декартового произведения ). Важнейшими новыми операциями являются инверсия (унарная операция) и композиция (бинарная операция).