Примеры решения задач

110. Найдите размерность поля многочленов GF(х³+1) над числовым полем GF(2), множество всех многочленов этого поля и произведение двух произвольных элементов поля по mod х³+1.

Решение. Характеристика числового поля GF(2) р=2. Она определяет размерность поля многочлена GF(х³+1): q= pⁿ=2³=8 (3 – степень многочлена х³+1). Т.о., множество всех многочленов этого поля состоит из 8-ми элементов: {0, 1, x, x+1, x², x²+1, x²+x, x²+x+1 }. Каждому элементу этого множества можно поставить в соответствие либо двоичное число: {000,001,010,011,100,101,110,111}, либо десятичное {0,1,2,3,4,5,6,7}.

Перемножим два произвольных элемента:

(x²+1) x²= x⁴+ x²= x⁴+ x²+0 =x⁴+ x²+2х= x⁴+х+x²+х=х(x³+1)+(x²+х)=x²+х.

Задачи для самостоятельного решения

110. Найдите размерность поля многочленов GF(х²+х+1) над числовым полем GF(2), множество всех многочленов этого поля и произведение двух произвольных элементов поля по mod х²+х+1.

111. Найдите размерность поля многочленов GF(х⁴+х³+1) над числовым полем GF(2), множество всех многочленов этого поля, сумму и произведение двух произвольных элементов поля по mod х⁴+х³+1.

112. Построить таблицы сложения и умножения для поля многочленов GF(х²+х+1) над числовым полем GF(2).

113. Построить таблицы сложения и умножения для поля многочленов GF(х³+1) над числовым полем GF(2).

114. Найдите размерность поля многочленов GF(х²+х+2) над числовым полем GF(3), множество всех многочленов этого поля и составьте таблицы сложения и умножения для элементов этого поля.

7.2.4.Поиск неприводимых многочленов поля gf(g(X)) над полем gf(р)

Пусть дано некоторое поле многочленов GF(q(х)) над числовым полем с характеристикой р, причем многочлен q(х) степени n. Обозначим через g₁(x), g₂(x), …, g_q-1(x) различные неприводимые многочлены, отвечающие примитивным корням: с₁, с₂, …, с_q-1.

Утверждение. Существует единственно возможное разложение многочлена x^q-1-1 на множители g_i(x); или, что одно и то же, каждый элемент с_i является корнем многочлена x^q-1-1; или, наконец, любой приводимый многочлен этого поля можно представить в виде произведения порождающего g(x) и проверочного h(x) многочленов.

где

Для проверочного многочлена h(x) берутся те степени с^j, которые не вошли в многочлен g(x).

Если с – примитивный корень многочлена g(x), то g(с)=g₀+g₁c+g₂c²+…+g_ncⁿ=0. Выразим из неё g_ncⁿ (учитываем, что g_n=1). Получим формулу, с помощью которой можно найти степени корней cⁿ, cⁿ⁺¹ и т.д.:

cⁿ=g₀+g₁c+g₂c²+…+g_n-1c^n-1,

cⁿ⁺¹=c cⁿ= g₀c+g₁c²+g₂c³+…+g_n-1cⁿ.

Алгоритм построения неприводимых многочленов в заданном поле.

1. Записать порождающий многочлен g(x) в виде произведения 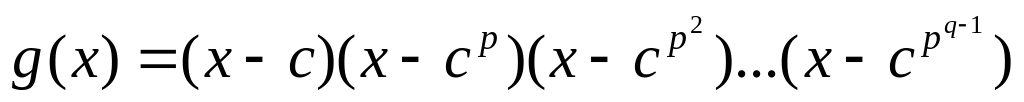, где с – примитивный корень, р – характеристика числового поля, q=pⁿ, n – степень многочлена модуля q(x).

2. В таблицу неприводимых многочленов, которую мы создаем, напротив степеней записываем многочлен q(x) и выражаем все остальные степени сⁱ через с¹, с², …, с^n-1.

3. Ищем неприводимые множители. Для этого:

   1. Берем произвольный корень a=cⁱ, niq-1, тогда (*).

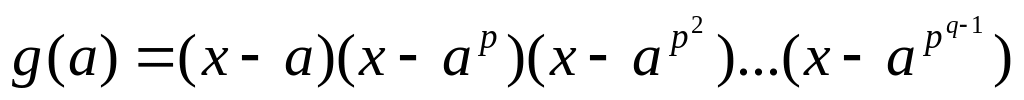   2. Находим выражение 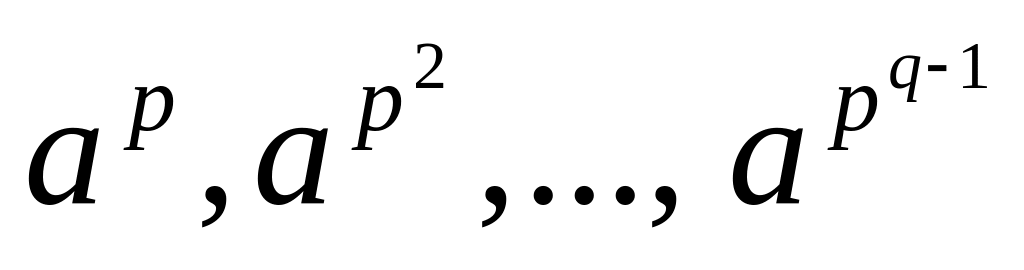через cⁱ и подставляем в (*).

   3. Раскрываем скобки, приводим подобные слагаемые (все действия выполнятся в поле многочленов по заданному модулю), в результате получим некоторый неприводимый многочлен степени не выше n и запишем его в таблицу против корней .

   4. Пункты а-с продолжаем выполнять до тех пор, пока не заполним всю таблицу.

4. Выполним проверку: .
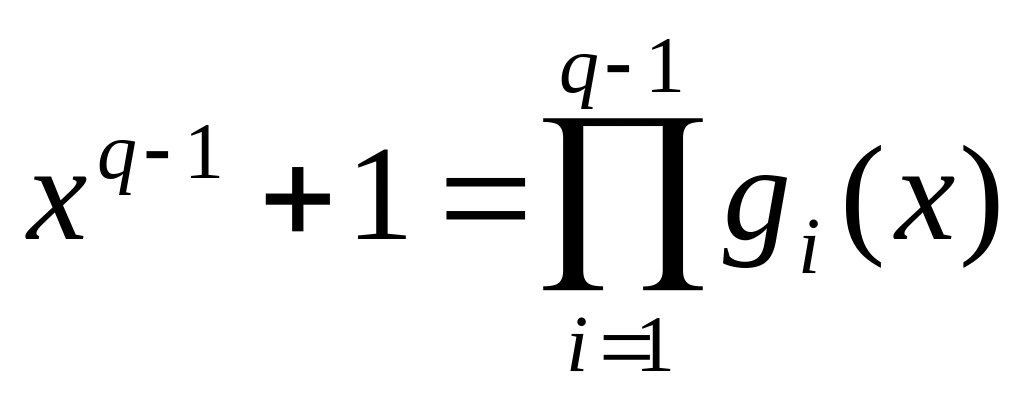