Примеры решения задач

110. Доказать, что алгебра <Q[2], +,  > является кольцом. Q[2]={a+b2 | a,bQ}.

Решение: Можно воспользоваться определением кольца, но так как множество действительных чисел по операциям сложения и умножения является кольцом, а Q[2]R, то воспользуемся критерием подкольца.

1. х,у Q[2]: х= a₁+b₁2, у= a₂+b₂2, х-у= a₁+b₁2- a₂-b₂2= a₁-a₂+(b₁-b₂)2.

a₁-a₂ Q и b₁-b₂ Q, следовательно, a₁-a₂+(b₁-b₂)2 Q[2].

2. ху= (a₁+b₁2)( a₂+b₂2)= a₁a₂+2b₁b₂+(a₁b₂+a₂b₁)2. a₁a₂+2b₁b₂ Q и a₁b₂+a₂b₁ Q, значит, ху Q.

Т.к. <Q[2], +,  > является подкольцом, то сама она является кольцом по определению.

Задачи для самостоятельного решения

110. Показать, что множество М чисел вида a+b3+c5, a,b,cZ является кольцом относительно операций «+» и « ».

111. Доказать, что множество упорядоченных пар (х,у), х,уR образуют кольцо по операциям  и : (a,b)(c,d)=(a+c, b+d); (a,b)(c,d)=(ac+5bd, ad+bc);

112. Докажите, что <M2, , > - кольцо, где M2 – множество всех квадратных матриц, а ,  - соответственно операции сложения и умножения матриц.

113. Пусть М множество матриц вида , a,bR. Доказать, что множество М по операциям матричного сложения и умножения является кольцом.

114. Докажите, что <Zm, , > - кольцо.

Примечание. Zm ={ }- фактормножество целых чисел по отношению сравнимости. :   Zm полагаем

:   Zm полагаем

7.1.4.Поле

Поле - основная алгебраическая структура. Кольцо Р называется полем, если выполняются следующие условия:

1. Кольцо является ассоциативным, коммутативным и имеет единицу, отличную от нуля.

2. Любой элемент кольца, а0 имеет обратный а^-1: аа^-1=а^-1 а=1.

Теорема (Критерий подполя). Для того, чтобы не пустое подмножество К базы поля Р образовывало по операциям из Р поле необходимо и достаточно:

1. К содержит более одного элемента;

2. К замкнуто по операциям «-» и «:» на ненулевой элемент.

Примеры решения задач

110. Доказать, что алгебра <Q[2], +,  > является полем. Q[2]={a+b2 | a,bQ}.

Решение: Ранее установлено, что это множество является кольцом. Это кольцо ассоциативно-коммутативное (это легко проверить) с единицей (нейтральный элемент по операции умножения е равен 1) отличной от 0. Остается выяснить: верно ли, что любой элемент не равный нулю, имеет обратный.

хQ[2]:хх^-1=е=1 х^-1= = . Покажем, что этот элемент находится в мн-ве Q[2]: = Q[2], т.к. R и R. Знаменатель отличен от нуля, т.к. если это не так и a²-2b²=0, то , а - рациональное число, которое не может равняться иррациональному 2. Т.о.показали, что данная структура поле.

Задачи для самостоятельного решения

110. Является ли множество целых чисел с обычными операциями сложения и умножения полем?

111. Является ли множество действительных чисел с обычными операциями сложения и умножения полем?

112. Является ли кортеж <R, , >, где ху=х+у-1 и ху=х+у-ху полем?

113. Является ли полем алгебра <G, +,  >? G= { 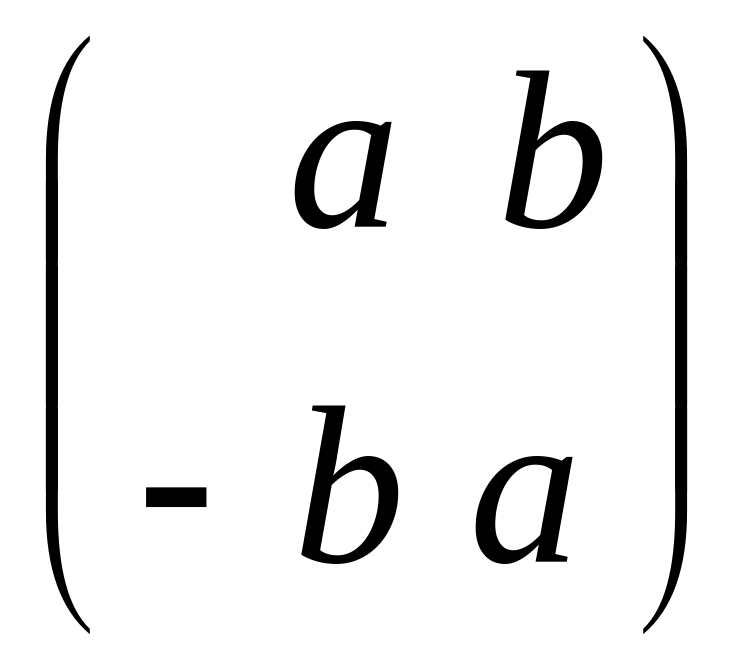| a,bR}.

114. Является ли <Z_m, , > - полем?

115. Докажите, что <Z₃, , > - поле.

116. Является ли <Zр, , > - полем (р – простое число)?

117. Доказать, что M=<{a+bi5 | a,bQ},+,  > является полем по арифметическим операциям «+» и « ».

118. Является ли полем <{0,1}, ,  >, 0 и 1 - бинарные элементы, для которых выполняются операции сложения по модулю 2 и умножения.