Глава 2.Элементы теории множеств

2.1.Основные понятия теории множеств

2.1.1.Обозначения и способы задания множеств

Понятие множества является первичным, то есть не выражается через другие понятия. Это фундаментальное неопределяемое понятие математики. Можно сказать, что множество – это любая определенная совокупность объектов. Объекты, из которых состоит множество, называются его элементами.

Обычно множество обозначают: А, В, С …, а его элементы: a, b, c …

Если объект х является элементом множества М, то говорят, что х принадлежит М и обозначают хМ . В противном случае, говорят, что х не принадлежит М и обозначают хМ.

Множество, не содержащее элементов, называется пустым. Пустое множество обозначают . Универсальным множеством называется множество U, которое содержит все всевозможные элементы.

Мощностью множества называется количество элементов в нем.

Перечислим способы задания множеств:

Перечислением элементов, если множество конечное, например {a, b, c }.

Заданием характеристического свойства, например {х| х-блондины}.

Равенство множеств А и В.

Множества А и В называют равными, если каждый элемент одного из них является элементом другого и обозначаются А=В.

Включение множеств.

Говорят, что множество А включается в множество В, если каждый элемент множества А является элементом множества В и обозначают АВ. Множество А называют подмножеством множества В, а множество В называют надмножеством множества А.

Примеры решения задач

5. Задайте множество А={x | х – целое неотрицательное и х+2=5} другим способом.

Решение: корень уравнения х+2=5 равен 3. Это число целое неотрицательное, следовательно, является элементом данного множества.

Ответ: А={3};

6. Выясните, равны ли множества:

   1. А={1, 2, 3}; В={2, 3, 1}.

   2. А – множество всех равносторонних треугольников; В – множество всех равноугольных треугольников.

   3. А={1, 5, 8}; В={2, 8}.

   4. А={0, 1}; В={{0, 1}}.

Решение.

a) А={1, 2, 3}; В={2, 3, 1}. Множества состоят из одних и тех же элементов, следовательно, А=В.

b) А – множество всех равносторонних треугольников; В – множество всех равноугольных треугольников. Т.к. в равностороннем треугольнике все углы равны, то А=В.

c) А={1, 5, 8}; В={2, 8}. АВ, т.к. в этих множествах различное количество элементов.

d) А={0, 1}; В={{0, 1}}. АВ, так как первое – двухэлементное, а второе - одноэлементное.

7. Даны множества N, Z, R. Укажите, какие из них являются подмножествами.

Решение: NZ, где N-множество натуральных чисел, а Z- целых чисел.

Z R, где R- множество действительных чисел.

Задачи для самостоятельного решения

8. Сколько элементов в множестве {1,{1},2,{1,{2,3}},}?

9. Определите мощность множества, состоящего из:

   1. букв слова «математика»;

   2. букв слова «перпендикулярные»;

   3. цифр числа «635252»;

   4. цифр числа «1010111».

10. Найдите более простое описание множеств (перечисляющее их элементы):

    1. А={x | х – целое и х²+4х=12};

    2. В={x | х – название дня недели, не содержащее буквы “е”};

    3. А={n² | n – целое}.

11. Перечислите элементы следующих множеств:

1. А={x | хZ и 10х17};

2. C={x | хZ и 6х²+x-1=0};

3. B={x | хZ и х²<24};

4. D={x | хR и 6х²+x-1=0}.

12. Определите с помощью характеристического свойства следующие множества:

1. S={2,5,8,11,…};

2. T= .

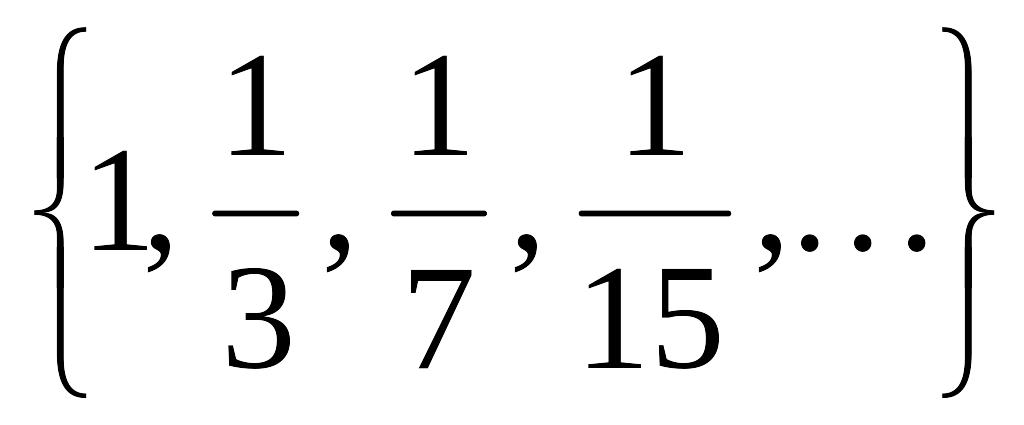13. Даны три множества А={0, 1}, B={{0,1}, С={{{0,1}, 2}, 3}. Верно ли, что: АВ, BC, но АС?

14. Верно ли, что:

1. 1{1,2};

2. 3{0,1};

3. 3;

4. ;

5. {};

6. {0,1}{{{0,1},2}, {1,2}, 0, 1};

7. {1,2}{{1,2}, 1, 2};

8. {1,2}{{1,2}}.

15. Привести примеры таких множеств А, В, С, D, что:

1. АВ, BD, DC, AD, BС;

2. АВ, D; BC, CD;

3. АВ, BС, СD;

4. АС, BC, АВ;

5. АС, BC, АВ, BС;

6. A={B}, BA.

16. Укажите все подмножества данных множеств:

1. {0,1}

2. {0,1,2};

3. {a,b,c};

4. {∆,◊,□};