Задачи для самостоятельного решения

110. Получить хеш-код для сообщения «HASHING» при помощи хеш-функции с параметрами p=17, q=19, кодируя буквы:

     1. порядковым номером в алфавите;

     2. ASCII – символами (HASHING: 72-65-83-72-73-78-71).

Задачи для повторения

110. Найдите остатки от деления:

1. (12371⁵⁶+34)²⁸ на 111;

2. 2³⁰⁰+2²⁰⁰ на 19.

110. Найдите последние две цифры чисел: .

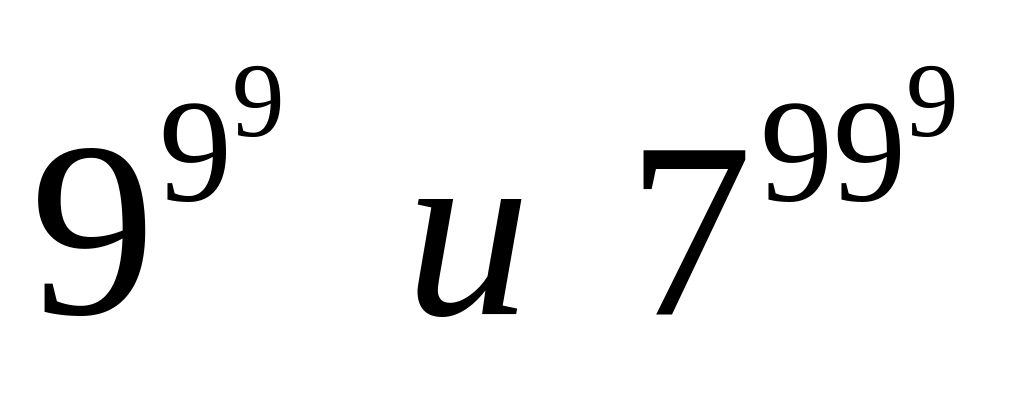111. Докажите, что 1+3^х+9^х делится на 13, если х=3n+1, n=0,1,2…

112. Доказать, что 2³ⁿ⁺¹+153²ⁿ+4⁴ⁿ 1 (mod 17).

113. Доказать, что если а¹⁰ⁿ+a^10m делится на 11, то а делится на 11.

114. Доказать, что (a+b)^p a^p+b^p (mod p).

115. Решите следующие сравнения:

1. 2х1 (mod 7);

2. 12x6 (mod 18);

3. 69x16 (mod 307);

4. 164x28 (mod 404);

5. 393x213 (mod 492).

6.2.Алгебра многочленов

6.2.1.Основные определения

Важное значение в теории чисел имеет понятие многочлена или полинома. Многочленом называется выражение вида

где аi, 0in - коэффициенты; х – переменная; n - степень многочлена, обозначаемая deg f(x).

Два многочлена равны тогда и только тогда, когда равны их соответствующие коэффициенты.

Теорема. Пусть f(x) и g(x) многочлены, тогда

.

Многочлен f(х) делится на многочлен g(x), если существует многочлен q(x) такой, что f(x)=q(x)g(x). В этом случае говорят, что многочлен g(x) - делитель многочлена f(x), а f(x) - кратное многочлена g(x).

Для многочлена f(x)=a₀+a₁x+…+a_nxⁿ коэффициент а₀ является постоянным членом. Многочлены степени называются постоянными многочленами - константами.

Теорема (алгоритм деления многочленов с остатком). Пусть g(x)0 некоторый многочлен. Тогда для каждого многочлена f(x) существует также многочлены q(x) и r(x), что f(x)=q(x)g(x)+r(x), где deg(r(x))<deg(g(x)).

Примеры решения задач

110. Найдите неполное частное и остаток от деления многочленов f(x)+х⁶+х³ и g(x)=х³+х²+1.

Решение. Запишем в стандартном виде f(x)= 1x⁶+0x⁵+0x⁴+1x³+0x²+0x+0.

_1x6+0x5+0x4+1x3+0x2+0x+0						x3+x2+1
x6+ x5+ x3						x3-x2+x-1 =q(x)
	_-x5+0x4+0x3+0x2+0x+0
	-x5- x4 - x2
		_x4+ 0x3 +x2+0x+0
			x4+1x3 +1x
			_ -1x3 +x2 - 1x +0
				-1x3 – x2 -1
				2x2 - 1x+1		=r(x), deg(r(x))<deg(g(x))

Т.о., f (x)=x⁶+x³=( x³+x²+1)  (x³-x²+x-1)+ 2x² -x+1.