Задачи для самостоятельного решения

110. С помощью решета Эратосфена найдите все простые числа от 1 до 50.

Примечание. Данный метод состоит в том, что из ряда чисел последовательно вычеркиваются все числа кратные 2, потом из оставшихся чисел вычеркиваются все числа, кратные 3 и т.д., до заданного числа N.

110. Представьте каноническое разложение следующих чисел: 18, 255, 467, 899, 7564532, 12345678.

6.1.2.Теорема о делении с остатком. Алгоритм Евклида

Теорема о делении с остатком. Если a и b>0 целые числа, то существуют единственные целые числа q и r такие, что a=bq+r_{, 0 r<b.}

_{Алгоритм Евклида (алгоритм нахождения НОД(a,b)).} Его содержание сводится к последовательному вычислению следующих равенств:

a=bq1+r1, 0<r1<b; b=r1q2+r2, 0<r2<r1; r1=r2q3+r3, 0<r3<r2; … … … … … … … rn-2=rn-1qn+rn, 0<rn<rn-1; rn-1=rnqn+1, rn=НОД(a,b);

Действие алгоритма прекращается тогда, когда полученный остаток равен нулю; последний ненулевой остаток (rn) равен наибольшему общему делителю. Из алгоритма Евклида следует, что для любых целых чисел а и b всегда существуют числа m и n такие, что НОД(a,b) представляется в виде линейной комбинации этих чисел: НОД(a,b)=rn=ma+nb.

_{Кроме того, отношение a/b можно представить в виде цепной дроби:}

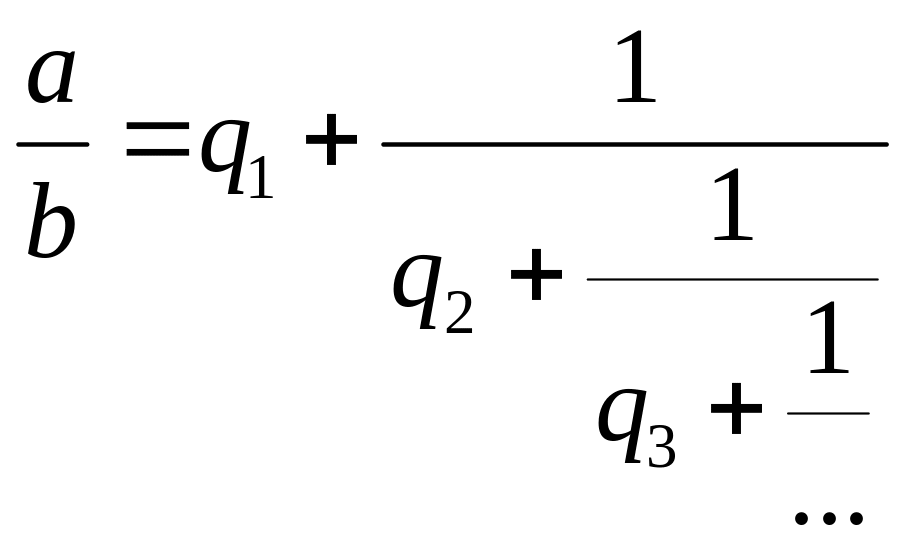
_{Теорема. Для того, чтобы уравнение ах+by=c, a,b,cZ было разрешимо необходимо и достаточно, чтобы c делилось на НОД(a,b).}

_{Теорема. Все решения в целых числах уравнения ах+by=c могут быть заданы формулами:}

_{, где tZ, а х0, у0 – частное решение уравнения.}

Примеры решения задач

110. Заданы два числа а=1656 и b=1150. Найдите НОД(a,b), составьте цепную дробь и линейную комбинацию.

     Решение. 1656=11501+506, 1150=5062+138, 506=1383+92, 138=921+46, 92=462; НОД(a,b)=46;

     46=138-92=138-(506-1383)=1384-506= =4(1150-5062)-506=41150-5069=41150- -9(1656-1150)=131150-91656. .

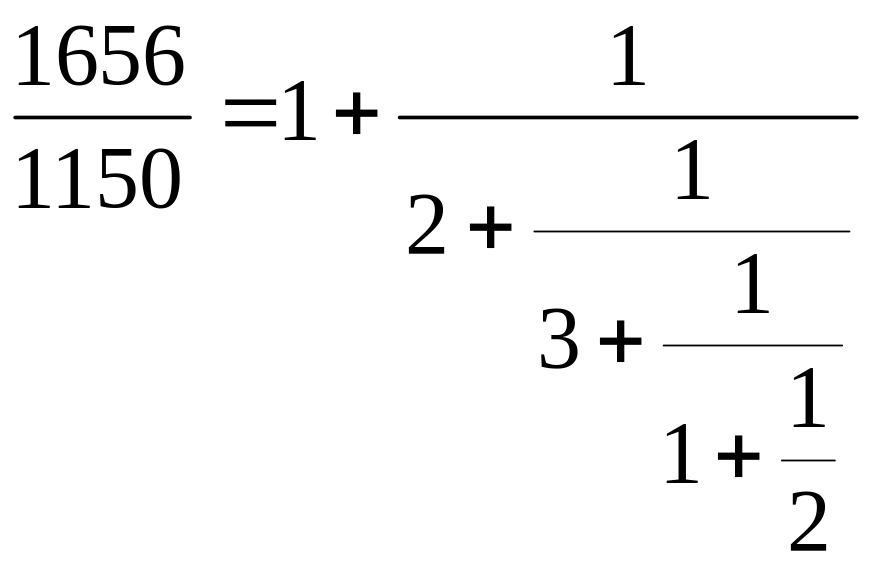111. Решить уравнения с двумя неизвестными.

а). 24х+16у=7; б). 21х-17у=5

Решение. а). Найдем НОД(24,16)=8. Проверим, делится ли 7 на НОД(24,16). Ясно, что 7 не делится на 8, следовательно, корней нет.

б). Найдем НОД(21,17)=1, 5 1. Данное уравнение всегда имеет решения и их бесконечно много. Составим линейную комбинацию в виде: НОД(21,17)=21m+17n. Запишем равенства:

21=171+4

17=44+1.

1=17-44=17-4(21-17)=17-421+417=17(1+4)-421=21(-4)+175. Получили:

21(-4)-17(-5)=1. Умножим его на 5:

21(-20)-17(-25)=5. Т.о., получили частные решения х₀=-20 и у₀=-25.

Общее решение получим из системы:

.

Задачи для самостоятельного решения

110. Найдите пары чисел q и r для пар a и b:

1. 123 и 15;

2. 218 и 7;

3. -8 и 11;

4. 26 и -16;

5. 115 и 8;

6. 12 и 211;

7. -48 и -23;

8. -56 и -127.

110. Поделить с остатком, используя алгоритм Евклида. Если возможно, найдите НОД(a,b), НОК(a,b), составьте цепную дробь и линейную комбинацию.

1. 218 на 43;

2. 57 на 13;

3. -114 на 32;

4. 93 на –15;

5. -131 на –17.

6. 846 на 246;

7. 115417 на 56341;

8. 9639 на 9163;

9. 464779 на 15946;

10. 5253 на 4641.

110. Найти решения уравнений с двумя неизвестными:

а). 6х-7у=3;

б). 8n-12m=4;

в). 3,5х+4,5у=53;

г). 11х+17у=150.

110. Для перевозки зерна имеются мешки вместимостью 60 и 80 кг. Сколько нужно и тех и других для перевозки 440 кг зерна?

111. Сколько надо сосудов емкостью по 0,5 и 0,8 литров для разлива 12 литров жидкости?