Задачи для самостоятельного решения

110. Найдите два остовных дерева в графе, изображенном на рис. 85.

111. Н 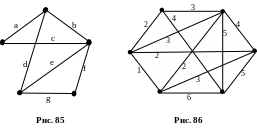айдите минимальный остов графа (рис. 86).

112. Изобразите граф на 7 вершинах и с 12 ребрами и постройте три различных остовных дерева.

113. В таблице дано расстояние (в милях) между пятью деревнями А, B, C, D и E. Найдите кратчайшее соединение (минимальное остовное дерево).

     	A	B	C	D	E
     A	-	13	3	9	9
     B	13	-	11	11	13
     C	3	11	-	9	7
     D	9	11	9	-	2
     E	9	13	7	2	-

114. В таблице приведены расстояния (в милях) между шестью городами Ирландии. Используя алгоритмы поиска минимального остовного дерева, найдите сеть дорог минимальной общей длины, связывающую все шесть городов.

     	Атлон	Дублин	Голуэй	Лимерик	Слайго	Уэксфорд
     Атлон	-	78	56	73	71	114
     Дублин	78	-	132	121	135	96
     Голуэй	56	132	-	64	85	154
     Лимерик	73	121	64	-	144	116
     Слайго	71	135	85	144	-	185
     Уэксфорд	114	96	154	116	185	-

115. Расстояние между потребителями электроэнергии А, Б, В, Г, Д, Е в десятках километров дано в таблице. Требуется построить сеть линий электропередач так, чтобы количество затраченных проводов было минимальным и можно было передать энергию из каждого города в любой другой.

     	А	Б	В	Г	Д	Е
     А	0	7	11	6	8	15
     Б	7	0	9	12	6	7
     В	11	9	0	3	7	3
     Г	6	12	3	0	2	4
     Д	8	6	7	2	0	1
     Е	15	7	3	4	1	0

116. Расстояние между городами А, Б, В, Г, Д, Е, Ж в сотнях километров дано в таблицах. Требуется построить сеть железных дорог так, чтобы количество затраченных рельсов было минимальным, и пассажир мог из каждого города попасть в любой другой. Укажите число возможных деревьев.

			а)									б)											в)
	А	Б	В	Г	Д	Е	Ж			А	Б	В	Г	Д	Е	Ж			А		Б		В		Г		Д		Е		Ж
А	0	5	11	6	8	15	8		А	0	5	11	6	3	15	8		А		0		6		11		6		8		8		8
Б	5	0	9	12	6	7	2		Б	5	0	7	12	6	7	2		Б		6		0		9		12		6		7		2
В	11	9	0	3	6	3	7		В	11	7	0	3	6	3	7		В		11		9		0		3		6		3		7
Г	6	12	3	0	2	4	13		Г	6	12	3	0	2	4	13		Г		6		12		3		0		2		3		13
Д	8	6	6	2	0	1	5		Д	3	6	6	2	0	2	5		Д		8		6		6		2		0		1		5
Е	15	7	3	4	1	0	4		Е	15	7	3	4	1	0	4		Е		8		7		3		3		1		0		3
Ж	8	2	7	13	5	4	0		Ж	8	2	7	13	5	4	0		Ж		8		2		7		13		5		3		0

			г)									д)									е)
	А	Б	В	Г	Д	Е	Ж			А	Б	В	Г	Д	Е	Ж			А	Б	В	Г	Д	Е	Ж
А	0	5	11	6	8	3	8		А	0	5	1	3	8	15	8		А	0	5	11	6	3	15	8
Б	5	0	9	12	5	7	2		Б	5	0	9	12	6	7	2		Б	5	0	9	12	4	7	2
В	11	9	0	2	6	3	7		В	1	9	0	3	5	3	7		В	11	9	0	3	6	3	7
Г	6	12	2	0	2	4	13		Г	3	12	3	0	2	4	11		Г	6	12	3	0	2	4	13
Д	8	5	6	2	0	1	5		Д	8	6	5	2	0	1	5		Д	3	4	6	2	0	11	5
Е	3	7	3	4	1	0	4		Е	15	7	3	4	1	0	4		Е	15	7	3	4	11	0	1
Ж	8	2	7	13	5	4	0		Ж	8	2	7	11	5	4	0		Ж	8	2	7	13	5	1	0

110. Н 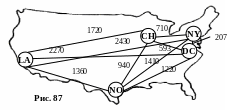а рис. 87 показаны расстояния между телевизионными центрами США. Найдите конфигурацию кратчайшей кабельной сети, которой их можно было бы соединить.

111. На графе G, изображенном на рис. 88, каждая вершина представляет некоторое лицо, а ребра (x_i, x_j) отражают тот факт, что лицо x_i может общаться с лицом x_j и наоборот. Требуется определить такой способ передачи конфиденциального сообщения между 12 лицами, при котором вероятность утечки информации будет наименьшей. Каждой передаче сообщения от x_i к x_j приписывается некоторая вероятность р_ij того, что послание может быть перехвачено посторонним лицом. Эти вероятности в процентах даны на рис. 88.

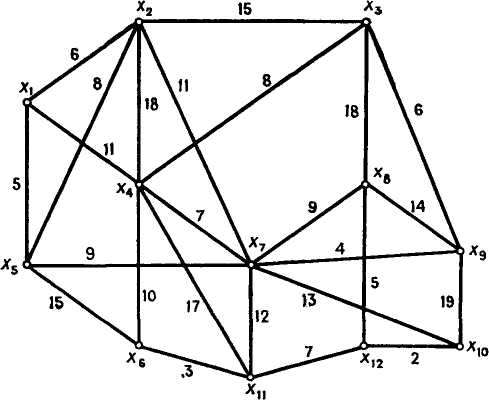
Примечание. Очевидно, что пути передачи сообщения должны образовывать остовное дерево графа G, и требуется найти такое остовное дерево, которое минимизирует величину 1-П(1-р_ij), где произведение берется по тем ребрам, которые образуют это дерево. Требуемое остовное дерево будет совпадать c минимальным остовом графом, при этом р_ij принимаются за «стоимости» ребер.