Задачи для самостоятельного решения
Определите
корни предложенных деревьев. Каково
их цикломатическое число?
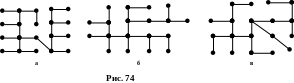Найдите
корни деревьев. Являются ли эти деревья
бинарными?Выясните, являются ли графы, задаваемые следующими матрицами смежности, деревьями:
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
Для графа, не являющегося деревом, найти количество остовов, используя матричную теорему о деревьях.
4.2.2.Алгоритм Краскала для построения минимального остовного дерева
Остовом (остовным деревом) связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом (говорят: «покрывающим его деревом»). Минимальное остовное дерево – это остов с наименьшей суммой весов ребер.
Алгоритм Краскала.
Сортируем ребра в порядке неубывания веса.
Берем первое ребро из списка, его концы помечаем меткой 1.
Просматриваем отсортированный список, при этом ребро включается в дерево, если оно не образует цикл с предыдущими.
если концы добавляемого ребра помечены одинаковыми ненулевыми метками, то ребро образует цикл, его не включаем.
если концы добавляемого ребра помечены меткой 0, то включаем это ребро, помечая вершины меткой, на единицу больше текущей метки.
если концы добавляемого ребра помечены разными ненулевыми метками, то включаем его в список, помечая все вершины с меньшей меткой меткой другой вершины.
если одна из меток рассматриваемого ребра 0, а другая не 0, то включаем это ребро, при этом нулевая вершина помечается меткой второго конца.
Повторяем пункт 3 до тех пор, пока все ребра не кончатся.
Такая задача возникает, например, в том случае, когда вершины являются клеммами электрической сети, которые должны быть соединены друг с другом с помощью проводов наименьшей общей длины (для уменьшения уровня наводок). Другой пример: имеется набор населенных пунктов. Требуется связать их телефонными линиями, если известна стоимость прокладки линии от одного населенного пункта до любого другого.