Задачи для самостоятельного решения
Постройте матрицу расстояний, определите диаметр, радиус, центры графов, изображенных на рисунке 58.
Рис. 58
Постройте матрицу расстояний, определите диаметр, радиус, центры графов, изображенных на рисунке 56.
4.1.7.Эйлеровы циклы
Цикл,
проходящий по каждому ребру графа ровно
один раз, называется Эйлеровым.
Граф, имеющий эйлеров цикл, тоже будем
называть эйлеровым. Эйлеровых графов
почти нет, т.е.
,
где G(n) –
множество всех графов, Gp(n)-
множество тех графов из G(n),
которые являются эйлеровыми.
Теорема. (Критерий эйлеровости графа). Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин – чётные числа.
Кроме понятия эйлерова цикла, в задачах часто возникает необходимость нахождения цепи, проходящей по каждому ребру ровно один раз (снимается требование замкнутости). Такие цепи будем называть эйлеровыми цепями. Задачи на проведение эйлеровых линий без повторений и без отрыва карандаша от бумаги являются одним из математических развлечений.
Теорема. В связном графе существует эйлерова цепь тогда и только тогда, когда граф содержит не более двух вершин нечётной степени.
Примеры решения задач
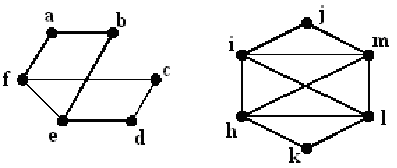
Имеются ли эйлеровы циклы в заданных графах?
Решение. Воспользуемся критерием эйлеровости графа. Степени всех вершин в графе на рис. 60 четны, поэтому этот граф имеет эйлеров цикл, например, h, l, i, m, h, i, j, m, l, k, h. |
Рис. 59 Рис. 60 |
Для первого графа (рис. 59) условия теоремы не выполняются, т.к. имеются две вершины, степень которых равна 3 (нечетная): e и f. Следовательно, данный граф эйлерова цикла не содержит.
Задачи для самостоятельного решения
Какие из графов, упоминающихся в задачах и примерах, являются эйлеровыми?
Имеют ли пятиугольник и пятигранник-пирамида с петлями в некоторых вершинах эйлеров цикл (цепь)?
4.1.8.Алгоритм построения Эйлерова цикла
Алгоритм построения эйлерова цикла:
1. Выберем в графе произвольный простой цикл и удалим его из графа.
2. В оставшемся графе снова выберем простой цикл, удалим его и т.д., в результате чего, исходный граф будет разобран на простые циклы.
3. Склеим полученные циклы в одно целое, отправляясь от некоторого цикла и приклеивая каждый новый цикл ровно в одной точке.
4.
Выпишем эйлеров цикл в исходном графе.
Примеры решения задач
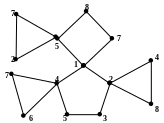
Найдите
эйлеров цикл для графа G,
изображенного на рис. 61.
Решение. Воспользуемся алгоритмом построения эйлерова цикла в графе.
Выберем цикл (1,2,3,5,4,1) и удалим его из графа, при этом удалятся вершины степени 2, ребра выбранного цикла, а степени вершин, входивших в этот цикл, уменьшатся на 2.
Из
оставшегося графа выбираем простой
цикл (1,5,8,7,1).Следующие простые циклы: (7,4,6,7), (2,4,8,2) и (7,2,5,7).
Склеим полученные циклы и выпишем эйлеров цикл в исходном графе: (1,5,2,7,5,8,7,1,2,4,8,2,3,5,4,6,7,4,1).