Примеры решения задач

Приведите пример маршрута, цепи, простой цепи, цикла, простого цикла. Решение. Маршрут a,b,c,a,d в графе является цепью, но не является простой цепью и циклом. Маршрут d,c,a,b – простая цепь, но не цикл. Маршрут a,b,c,d – простой цикл, но не цепь.

Рис. 54

Задачи для самостоятельного решения

110. З 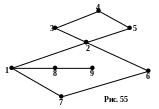адан граф и последовательности вершин (рис. 55). Определите, какие из этих последовательностей являются маршрутами, цепями, простыми цепями, циклами, простыми циклами?

     1. (1, 2, 3, 4, 5,2,1,7,6,2,1,7,6);

     2. (6,7,1,2,6);

     3. (1,2,3,4,5,2,1,7,6);

     4. (1,2,3,4,5,2,6);

     5. (1,2,6);

     6. (1,7,6);

     7. (1,2,3,4,5,2,3,4,5,2,6,7,1,2,6,7,1);

     8. (1,2,3,4,5,2,6,7,1);

     9. (1,2,6,7,1);

Рис. 56

110. На рис. 56 заданы графы G. Выполните следующие упражнения:

     1. Составьте матрицу смежности.

     2. Постройте матрицу инцидентности.

     3. Укажите степени вершин графа и его цикломатическое число.

     4. Составьте три маршрута длины 5, различные цепь и простую цепь, соединяющие вершину V₂ и вершину V₅.

     5. Постройте простой цикл, содержащий вершину V₄.

4.1.6.Расстояния в графе, центры графа

Расстоянием между двумя вершинами в графе G = <V,Х> называется длина кратчайшего маршрута, их связывающего. Матрица расстояний – квадратная матрица nn вида:

		V1	…	Vj	…	Vn		d(Vi, Vj) –расстояние между вершинами Vi и Vj
V1				:
…				:
Vi		. .	. .	d(Vi, Vj)
…
Vn

Диаметром графа D называется наибольшее из расстояний между вершинами графа. циклом.

Вершина, наибольшее из расстояний от которой до остальных вершин графа является наименьшим, называется центром графа, а расстояния – радиусами R. Если D=R, то все вершины центры.

Примеры решения задач

110. Постройте матрицу расстояний, определите диаметр, радиус, центры графа, изображенного на рисунке 57.

Рис. 57

Решение. Строим матрицу расстояний 66.

		1	2	3	4	5	6		max	В каждой строке находим максимальное расстояние и выписываем его в столбец max. Максимальное число в столбце max – диаметр. Минимальное число в столбце max – радиус. Вершины, где в столбце max минимум – центры. В данной задаче: D=4, R=2, центр – вершина 3.
1		0	1	2	2	3	4		4
2		1	0	1	1	2	3		3
3		2	1	0	1	1	2		2
4		2	1	1	0	2	3		3
5		3	2	1	2	0	1		3
6		4	3	2	3	1	0		4