
- •Оглавление
- •Глава 5. Основы математической теории информации 58
- •Глава 6. Элементы теории чисел 74
- •6.2.1. Основные определения 83
- •Глава 7. Алгебраические структуры 87
- •Введение
- •Глава 1.Введение
- •1.1.Основные понятия криптографии
- •1.1.1.История развития криптографии
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •1.1.2.Сложность алгоритмов
- •1.1.3.Стойкость криптографических систем
- •Глава 2.Элементы теории множеств
- •2.1.Основные понятия теории множеств
- •2.1.1.Обозначения и способы задания множеств
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •2.1.2.Операции над множествами
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •2.1.3.Прямое произведение множеств
- •П римеры решения задач
- •Задачи для самостоятельного решения
- •2.2.Отношения между множествами
- •2.2.1.Определение бинарных отношений
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •2.2.2.Представление бинарных отношений в виде графа, матрицы
- •Примеры решения задач
- •Построенная таблица есть таблица бинарного отношения. Задачи для самостоятельного решения
- •2.2.3.Свойства бинарных отношений, отношение эквивалентности
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вопросы для повторения
- •Глава 3.Булева алгебра
- •3.1.Булевы функции
- •3.1.1.Понятие булевой функции
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3.1.2.Суперпозиция функций
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3.1.3.Двойственные функции
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3.1.4.Логические схемы
- •Примеры решения задач
- •3.2.Нормальные формы
- •3.2.1.Разложение функций по переменным
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3.2.2.Минимизация нормальных форм, карты Карно
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Полиномы Жегалкина, алгоритм их построения для произвольных функций
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3.3.Полные системы функций
- •3.3.1.Полнота множества функций
- •Примеры решения задач
- •Глава 4.Элементы теории графов
- •4.1.Основные понятия теории графов
- •4.1.1.Способы задания графов, основные определения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.2.Числовые характеристики графов
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.3.Операции с графами
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.4.Изоморфизм графов
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.6.Расстояния в графе, центры графа
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.7.Эйлеровы циклы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.8.Алгоритм построения Эйлерова цикла
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.9.Гамильтоновы циклы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.10.Алгоритм построения гамильтонова цикла в графе
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.2.2.Алгоритм Краскала для построения минимального остовного дерева
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.2.3.Обходы дерева
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Задачи для повторения
- •Вопросы для повторения
- •Глава 5.Основы математической теории информации
- •5.1.Меры информации
- •5.1.1.Мера Хартли
- •Примеры решения задач
- •5.1.2.Мера Шеннона
- •Примеры решения задач
- •5.1.3.Единицы измерения количества информации
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •5.2.2.Код Хаффмана
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •5.3. Помехоустойчивое кодирование
- •5.3.1. Код с проверкой на четность
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •5.3.2.Коды с повторением
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •5.3.3.Групповой код Хемминга
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •5.3.4.Помехозащищенность кода
- •Примеры решения задач
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6.1.2.Теорема о делении с остатком. Алгоритм Евклида
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6.1.3.Отношение сравнимости
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6.1.4.Алгебра вычетов
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6.1.5.Решение сравнений вида ахb(mod m)
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6.1.6.Применение алгебры вычетов к простейшим шифрам
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6.1.7.Построение и использование хеш-функций
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Задачи для повторения
- •6.2.Алгебра многочленов
- •6.2.1.Основные определения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6.2.2.Нод многочленов
- •Примеры решения задач
- •Задачи для самостоятельного решения.
- •6.2.3.Разложение многочлена на множители
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вопросы для повторения
- •Глава 7.Алгебраические структуры
- •7.1.Основные понятия и свойства алгебраических структур
- •7.1.1.Алгебра
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.1.2.Группа
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.1.3.Кольцо
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.1.4.Поле
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.1.5.Конечные поля
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.2.Многочлены над конечными полями
- •7.2.1.Каноническое разложение многочлена
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.2.2.Порядок многочлена над конечным полем
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.2.3.Сравнение многочленов по данному модулю
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.2.4.Поиск неприводимых многочленов поля gf(g(X)) над полем gf(р)
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.3.Генераторы псевдослучайных последовательностей
- •7.3.1.Понятие псевдослучайной последовательности чисел
- •7.3.2.Практические методы получения псевдослучайных чисел
- •Задачи для самостоятельного решения
- •7.3.3.Понятие линейной последовательности
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.3.4. Периодичность линейных рекуррентных последовательностей
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.3.5.Связь линейных рекуррентных последовательностей над конечными полями с многочленами
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вопросы для повторения
- •214018, Г. Смоленск, проспект Гагарина, 56, т.: (0812) 55 – 41 – 04.
Примеры решения задач
Н
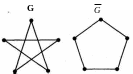 айдите
дополнение заданного графа G.
айдите
дополнение заданного графа G.
Решение. В заданном графе пять вершин. Чтобы построить его дополнение, поступим в соответствии с определением следующим образом: отмечаем все пять вершин и проводим только те ребра, которых нет в исходном графе.
Даны графы G1 и G2. Найдите объединение и пересечение этих графов.
Решение. Придерживаясь соответствующих определений, получаем следующие графы.

Задачи для самостоятельного решения
Изобразите дополнение, если задана матрица смежности графа:
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
Опишите матрицу смежности дополнения полного графа Кn.
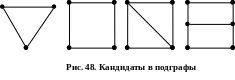 Какие
из графов на рис. 48 могут являться
подграфами графа из (предыдущей) задачи
152?
Какие
из графов на рис. 48 могут являться
подграфами графа из (предыдущей) задачи
152?Н
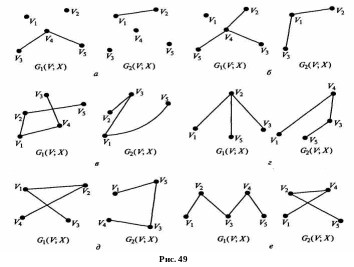 айдите
объединение, пересечение и дополнение
графов G1
и G2
(рис. 49).
айдите
объединение, пересечение и дополнение
графов G1
и G2
(рис. 49).Изобразите граф на 6 вершинах и с 16 ребрами и выполните с ним следующие упражнения:
Изобразите подграф на 3 вершинах и с 10 ребрами.
Изобразите остовный подграф.
Изобразите подграф, порожденный множеством вершин V1, V3, V5, V6.
4.1.4.Изоморфизм графов
Понятие изоморфизма для графов имеет наглядное толкование. Представим рёбра графов эластичными нитями, связывающими узлы – вершины. Тогда, изоморфизм можно представить как перемещение узлов и растяжение нитей. Изоморфные графы будем считать неразличимыми.
Чтобы доказать, что соответствующие графы G1 и G2 изоморфны, достаточно указать соответствующий изоморфизм. Если же требуется доказать, что графы не изоморфны, то приходится перебирать все возможные взаимнооднозначные соответствия между множествами вершин (при |V1|=|V2|=n таких соответствий будет n!) или же находить устойчивые характеристики графов, не совпадающие у G1 и G2.
Если дополнения графов изоморфны между собой, то исходные графы также будут изоморфны. При сложном изображении графов легче установить изоморфизм их дополнений.
Свойства графа, сохраняющиеся при изоморфизмах (число вершин, число ребер, число вершин заданной степени, число циклов заданной длины и т.д.) называются инвариантами. К сожалению, полная система инвариантов (такой их набор, что совпадение всех инвариантов из этого набора для G1 и G2 гарантирует, что они изоморфны) до сих пор неизвестна.
Примеры решения задач
Покажите, что следующие два графа изоморфны.

Решение. Отображение, являющееся изоморфизмом легко представить как модификацию первого графа, передвигающую вершину d в центр рисунка.
Рис. 50
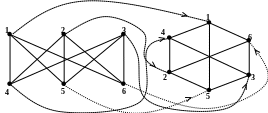 Изоморфны
ли следующие два графа?
Изоморфны
ли следующие два графа?
Решение. Заданные графы изоморфны. Один из возможных в данном случае изоморфизмов задан нумерацией вершин и для наглядности показан стрелками.
Задачи для самостоятельного решения
Проверьте, изоморфны ли графы.

Какие графы на рисунке 51 изоморфны между собой?
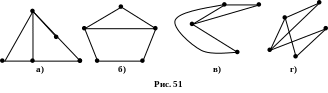 Постройте
изоморфизм графов.
Постройте
изоморфизм графов.

Определите, изоморфны ли графы на рис. 52. Построить их матрицы смежности.

Изоморфны ли графы, представленные на рис.53 между собой. Если да,
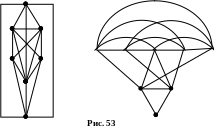 то
укажите изоморфизм.
то
укажите изоморфизм.
4.1.5.Маршрут, виды маршрутов
Маршрутом в графе G = <V,Х> называется последовательность вершин вида v0, v1, ..., vn-1, vn, где viV, i [0,n]. Вершины v0, vn называются связанными данным маршрутом (или просто связанными). Вершину v0 называют началом, а vn – концом маршрута. Если v0 = vn, то маршрут называют замкнутым. Число n называется длиной маршрута.
Маршрут, в котором все рёбра попарно различны, называется цепью. Замкнутый маршрут, являющийся цепью, называется циклом. Маршрут, в котором все вершины попарно различны, называется простой цепью. Цикл, в котором все вершины, кроме первой и последней, попарно различны, называется простым циклом.
