Глава 4.Элементы теории графов

4.1.Основные понятия теории графов

4.1.1.Способы задания графов, основные определения

Способы задания графов:

1. Явное задание графа как алгебраической системы.

2. Геометрический

3. Матрица смежности

4. Матрица инцидентности

1.Граф проще определять как модель, носителем которой является множество вершин, а отношение – бинарное отношение смежности вершин. Тогда данный граф запишется как <{a,b,c,d}; {(a,b), (b,a),(b,c),(c,b),(a,c),(c,a),(c,d),(d,c)}>. В таком представлении ребру соответствуют две пары вершин (v₁,v₂) и (v₂,v₁), инцидентных данному ребру. Чтобы задать такое представление, достаточно для каждого ребра указать двухэлементное множество вершин – его мы и будем отождествлять с ребром. Для данного графа рёбра задаются множеством {{a,b},{b,c},{a,c},{c,d}} и граф мы будем записывать как пару (V,Х), где V – множество вершин, а Х – множество рёбер.

2. Геометрический		3.Матрица смежности						4. Матрица инцидентности
			a	b	c	d			(a,b)	(a,c)	(b,c)	(c,d)
		a	0	1	1	0		a	1	1	0	0
		b	1	0	1	0		b	1	0	1	0
		c	1	1	0	1		c	0	1	1	1
		d	0	0	1	0		d	0	0	0	1
Рис. 40

Две вершины графа v_i и v_j называют смежными, если существует ребро их соединяющее.

Степенью вершины назовём удвоенное количество петель, инцидентных этой вершине плюс количество остальных инцидентных ей рёбер. Степень вершины будем обозначать deg v. Если deg v=1, то эта вершина называется висячей. Если deg v=0, то вершина называется изолированной.

Теорема Эйлера (о сумме степеней вершин графа). Сумма степеней всех вершин графа равна удвоенному числу ребер .

Следствие: Число нечетных вершин любого графа четно.

Это следствие имеет немало любопытных приложений.

1. Нечетное число знакомых в любой компании всегда четно.

2. Число вершин многогранника, в которых сходится нечетное число ребер, четно.

3. Число всех людей, когда-либо пожавших руку другим людям, нечетное число раз, является четным.

Граф называется связным, если любые его две вершины можно соединить маршрутом.

Компонентами связности графа называются подграфы данного графа, вершины которых являются классами эквивалентности отношения связанности в данном графе.

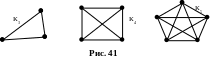Пустым называется граф без рёбер. Полным называется граф, в котором каждые две вершины соединены единственным ребром и обозначается К_n.

Граф называется взвешенным, если каждому ребру приписаны веса (стоимости).

Если в множестве Х разрешается повторять пары и разрешаются пары вида (v_i, v_i) – петля, то такой граф называется псевдографом. Если в графе есть кратные ребра, но петли запрещены, то такой граф называют мультиграфом.

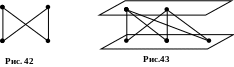Граф называется регулярным степени R (рис. 42), если степень каждой его вершины равняется R. Граф называется двудольным (рис. 43), если множество его вершин можно разбить на 2 подмножества так, что никакие две вершины одного подмножества не связаны.

Теорема. Граф будет двудольным тогда и только тогда, когда в нем нет циклов нечетной длины.