Задачи для самостоятельного решения

110. По заданной СДНФ функций построить полином Жегалкина:

     1. ;

     2. .

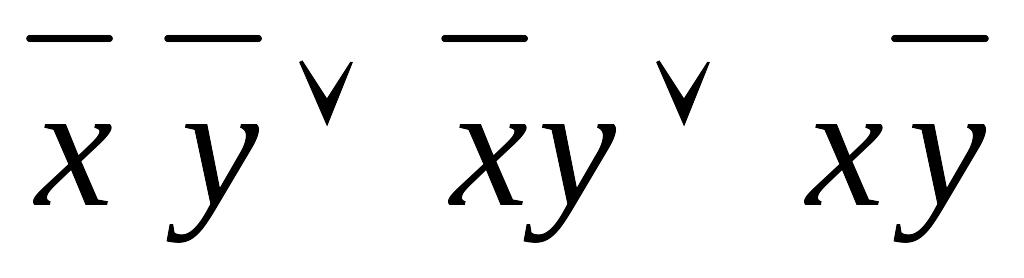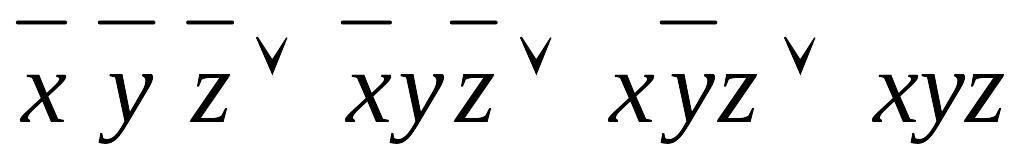111. Построить полином Жегалкина с помощью СДНФ для функций:

1. ;

2. ;

3. ;

4. .

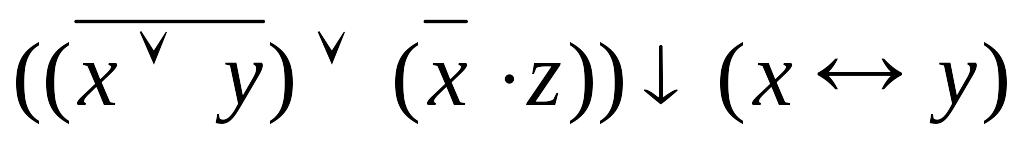110. Построить полином Жегалкина двумя способами для функций:

1. ;

2. 

3. ;

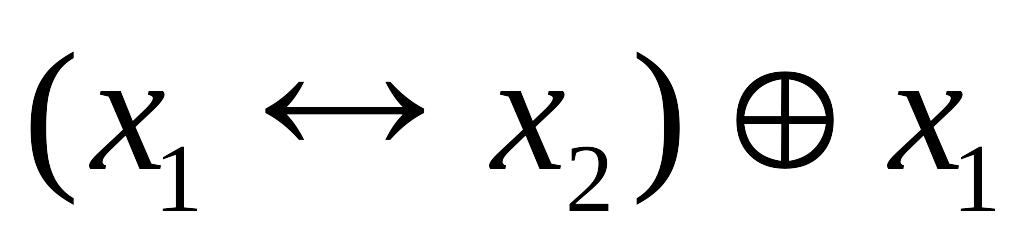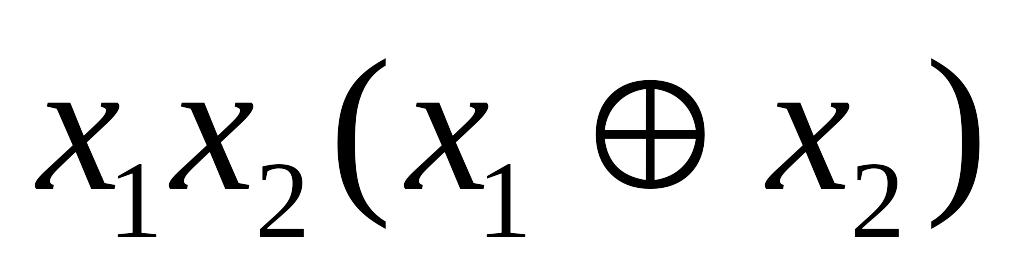4. f(x, y, z)=(1,0,0,1,0,0,0,1).

110. Заданы следующие функции:

1. f(x,y)=(0,1,0,1);

2. ;

3. .

   1. Построить для них полином Жегалкина.

   2. Выясните, имеют ли построенные полиномы следующий линейный вид: а₀+а₁х₁+а₂х₂+…+а_nx_n, . Такие функции называются линейными.

   3. Построить для заданных функций двойственные им. Выясните, являются ли они самодвойственными.

3.3.Полные системы функций

3.3.1.Полнота множества функций

Система функций {f₁, f₂, …, f_n} называется полной, если любую функцию булевой алгебры можно реализовать в виде формулы над этой системой функций.

Система - полная. Это следует из теоремы о представлении функции в виде СДНФ.

Теорема. Пусть даны две системы функций: F={f₁, f₂, …} и G={g₁, g₂, …}. Если система F полна и все функции из F можно выразить в виде суперпозиции функций системы G, то система G тоже полна.

Примеры решения задач

110. Доказать, что система функций - полная.

Доказательство: Известно, что F= - полна. Чтобы доказать, что G= - полна, нужно выразить любую функцию через функции системы G: , а дизъюнкция и отрицание из F есть в системе G.

110. Доказать, что система функций 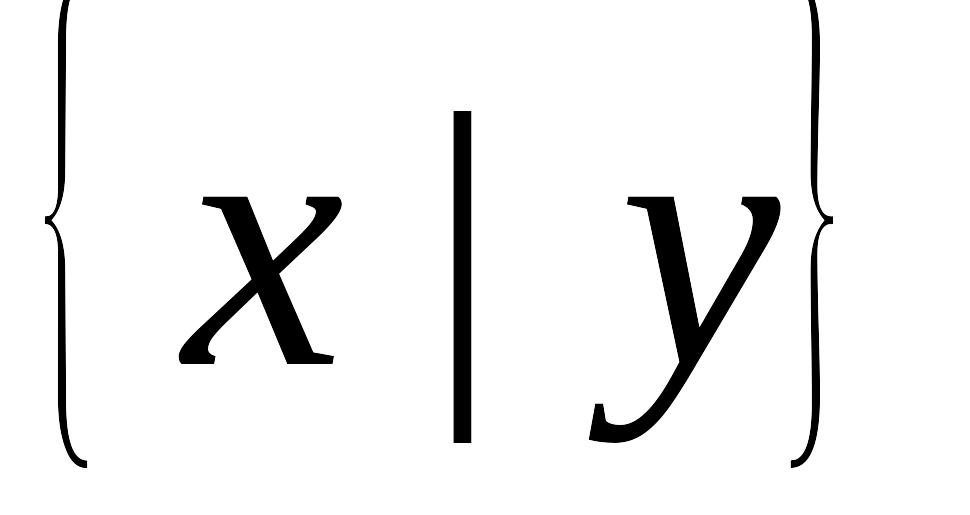полна.

Решение. Известно, что F= -полная. Выразим конъюнкцию и отрицание через штрих Шеффера:

Задачи для самостоятельного решения

110. Доказать, что следующие системы функций полные:

1. ;

2. ;

3. .

4. .

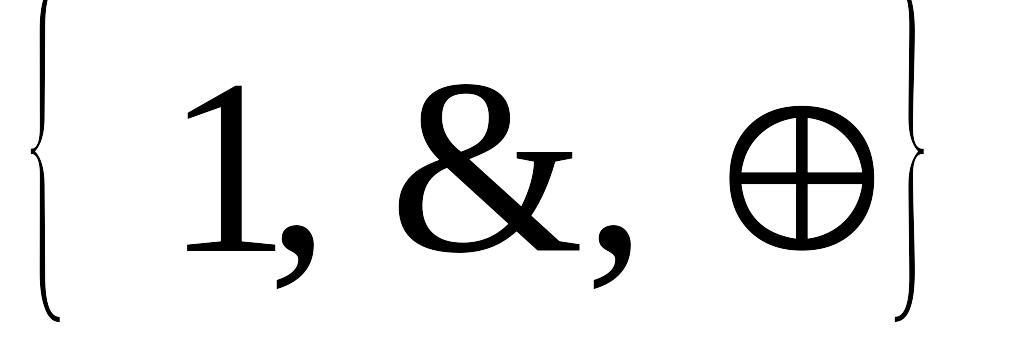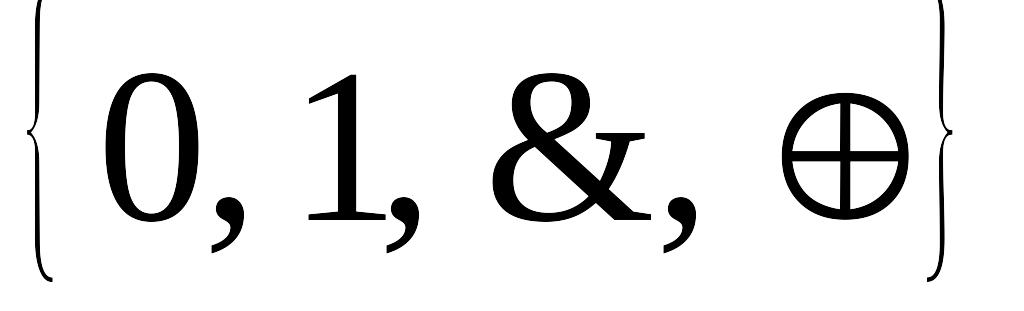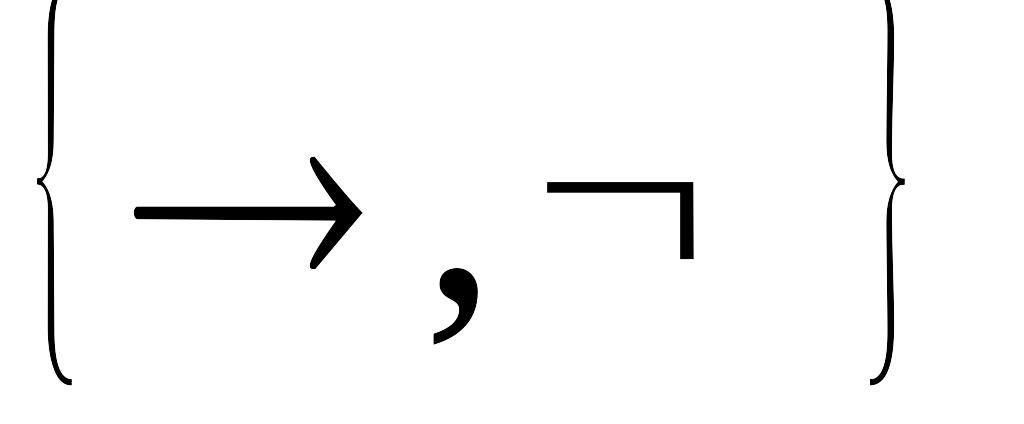3.3.2.Базисы

Полная система функций F={f₁, f₂, …} является базисом, если она минимальная, то есть F – полная, а F^/=F\{f_i} – не полна для любой .

Например, - полна, но не базис, так как - также полна.

Примеры решения задач

110. Выясните, является ли система функций базисом.

Решение. - базис. Так как - полна и и не полны.

Задачи для самостоятельного решения

110. Выясните, являются ли системы функций базисами.

1. _;

2. _;

3. ;

4. ;

5. .

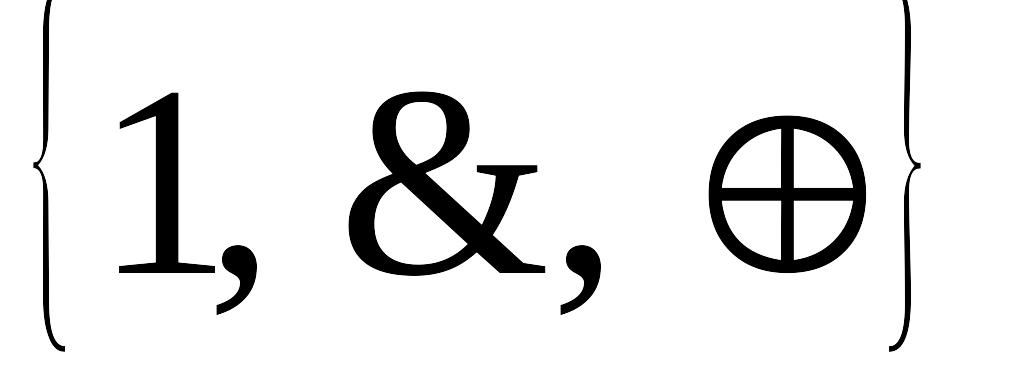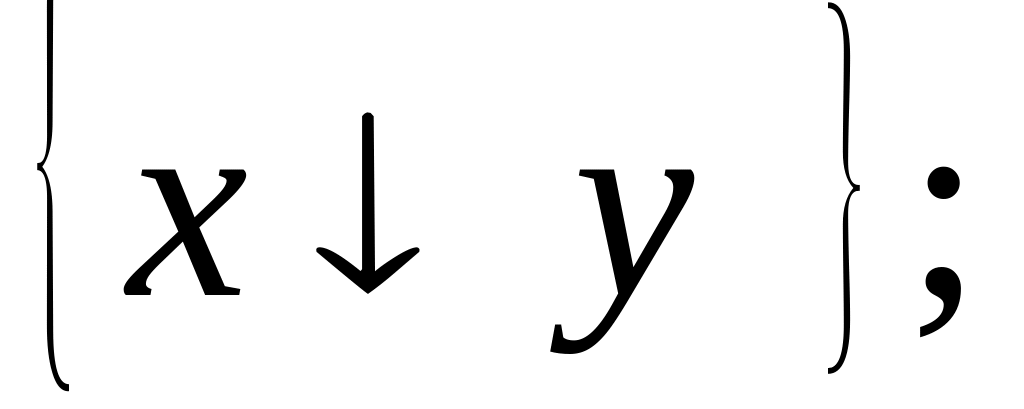Вопросы для повторения

1. Понятие булева функция. Булевы функции от двух переменных, их таблицы истинности.

2. Способы задания булевых функций. Определения эквивалентных формул. Примеры.

3. Основные тождества булевой алгебры. Примеры их использования.

4. Понятие функции, двойственной к данной. Пример нахождения функции, двойственной к данной.

5. Понятие самодвойственной функции. Алгоритм проверки, является ли функция самодвойственной. Пример.

6. Понятие элементарной дизъюнкции. Теорема о представлении функции в виде СКНФ. Алгоритм приведения булевой функции к СКНФ. Пример.

7. Понятие элементарной конъюнкции. Теорема о представлении функции в виде СДНФ Алгоритм приведения булевой функции к СДНФ. Пример.

8. Понятие минимальной ДНФ. Способы получения минимальной ДНФ. Пример.

9. Алгебра Жегалкина. Свойства операций. Пример.

10. Алгоритм представления булевой функции в виде многочлена Жегалкина. Примеры.

11. Понятие полная система функций. Теорема о полноте системы функций. Примеры полных и неполных систем.

12. Понятие базис полной системы функций. Примеры.

13. Построение логической схемы функции.