
- •Оглавление
- •Глава 5. Основы математической теории информации 58
- •Глава 6. Элементы теории чисел 74
- •6.2.1. Основные определения 83
- •Глава 7. Алгебраические структуры 87
- •Введение
- •Глава 1.Введение
- •1.1.Основные понятия криптографии
- •1.1.1.История развития криптографии
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •1.1.2.Сложность алгоритмов
- •1.1.3.Стойкость криптографических систем
- •Глава 2.Элементы теории множеств
- •2.1.Основные понятия теории множеств
- •2.1.1.Обозначения и способы задания множеств
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •2.1.2.Операции над множествами
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •2.1.3.Прямое произведение множеств
- •П римеры решения задач
- •Задачи для самостоятельного решения
- •2.2.Отношения между множествами
- •2.2.1.Определение бинарных отношений
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •2.2.2.Представление бинарных отношений в виде графа, матрицы
- •Примеры решения задач
- •Построенная таблица есть таблица бинарного отношения. Задачи для самостоятельного решения
- •2.2.3.Свойства бинарных отношений, отношение эквивалентности
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вопросы для повторения
- •Глава 3.Булева алгебра
- •3.1.Булевы функции
- •3.1.1.Понятие булевой функции
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3.1.2.Суперпозиция функций
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3.1.3.Двойственные функции
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3.1.4.Логические схемы
- •Примеры решения задач
- •3.2.Нормальные формы
- •3.2.1.Разложение функций по переменным
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3.2.2.Минимизация нормальных форм, карты Карно
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Полиномы Жегалкина, алгоритм их построения для произвольных функций
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3.3.Полные системы функций
- •3.3.1.Полнота множества функций
- •Примеры решения задач
- •Глава 4.Элементы теории графов
- •4.1.Основные понятия теории графов
- •4.1.1.Способы задания графов, основные определения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.2.Числовые характеристики графов
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.3.Операции с графами
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.4.Изоморфизм графов
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.6.Расстояния в графе, центры графа
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.7.Эйлеровы циклы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.8.Алгоритм построения Эйлерова цикла
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.9.Гамильтоновы циклы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.1.10.Алгоритм построения гамильтонова цикла в графе
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.2.2.Алгоритм Краскала для построения минимального остовного дерева
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4.2.3.Обходы дерева
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Задачи для повторения
- •Вопросы для повторения
- •Глава 5.Основы математической теории информации
- •5.1.Меры информации
- •5.1.1.Мера Хартли
- •Примеры решения задач
- •5.1.2.Мера Шеннона
- •Примеры решения задач
- •5.1.3.Единицы измерения количества информации
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •5.2.2.Код Хаффмана
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •5.3. Помехоустойчивое кодирование
- •5.3.1. Код с проверкой на четность
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •5.3.2.Коды с повторением
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •5.3.3.Групповой код Хемминга
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •5.3.4.Помехозащищенность кода
- •Примеры решения задач
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6.1.2.Теорема о делении с остатком. Алгоритм Евклида
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6.1.3.Отношение сравнимости
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6.1.4.Алгебра вычетов
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6.1.5.Решение сравнений вида ахb(mod m)
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6.1.6.Применение алгебры вычетов к простейшим шифрам
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6.1.7.Построение и использование хеш-функций
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Задачи для повторения
- •6.2.Алгебра многочленов
- •6.2.1.Основные определения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6.2.2.Нод многочленов
- •Примеры решения задач
- •Задачи для самостоятельного решения.
- •6.2.3.Разложение многочлена на множители
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вопросы для повторения
- •Глава 7.Алгебраические структуры
- •7.1.Основные понятия и свойства алгебраических структур
- •7.1.1.Алгебра
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.1.2.Группа
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.1.3.Кольцо
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.1.4.Поле
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.1.5.Конечные поля
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.2.Многочлены над конечными полями
- •7.2.1.Каноническое разложение многочлена
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.2.2.Порядок многочлена над конечным полем
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.2.3.Сравнение многочленов по данному модулю
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.2.4.Поиск неприводимых многочленов поля gf(g(X)) над полем gf(р)
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.3.Генераторы псевдослучайных последовательностей
- •7.3.1.Понятие псевдослучайной последовательности чисел
- •7.3.2.Практические методы получения псевдослучайных чисел
- •Задачи для самостоятельного решения
- •7.3.3.Понятие линейной последовательности
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.3.4. Периодичность линейных рекуррентных последовательностей
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7.3.5.Связь линейных рекуррентных последовательностей над конечными полями с многочленами
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Вопросы для повторения
- •214018, Г. Смоленск, проспект Гагарина, 56, т.: (0812) 55 – 41 – 04.
Задачи для самостоятельного решения
Какие переменные являются фиктивными, а какие существенными?
f = (1,1,1,1,0,0,0,0);
f = (0,0,1,1,0,0,1,1);
f = (0,0,1,1,1,1,0,0);
f = (0,1,0,1,0,1,0,1);
f = (1,1,0,0,1,1,0,0);
f = (1,1,1,0,1,0,1,1).
Укажите существенные и фиктивные переменные функции f(x,y,z), заданной вектором значений:
f = (1,1,0,0,0,0,1,1);
f = (1,0,0,1,1,0,0,0);
f = (0,0,0,1,1,0,0,0);
f = (1,0,0,1,1,0,0,1);
Постройте таблицу функции f:
Найдите количество функций n переменных, принимающих значение 1 ровно на одном наборе.
Найдите количество функций n переменных, принимающих на противоположных наборах одинаковые значения.
3.1.2.Суперпозиция функций
Суперпозицией булевых функций f0 и f1, ..., fn называется функция f(x1,...,xm) = f0(g1(x1,...,xm), ..., gk(x1,...,xm)), где каждая из функций gi(x1, ..., xm) либо совпадает с одной из переменных (тождественная функция), либо – с одной из функций f1, ..., fn.
Другими словами, суперпозиция – это подстановка функции в функцию. Например, функция f(x,y) = (x & y) является суперпозицией функций и &.
Одна и та же функция может быть реализована различными формулами, которые будем называть равносильными.
Следующие равносильности могут быть проверены прямым сравнением значений функций в левой и правой части соотношения на всевозможных наборах аргументов.
x & y = y & x;
 ;
;
 ;
;x & (y & z) = (x & y) & z;
 ;
;
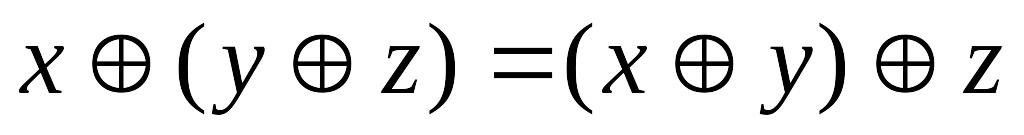 ;
; ;
;
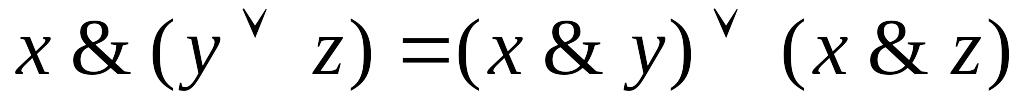 ;
;
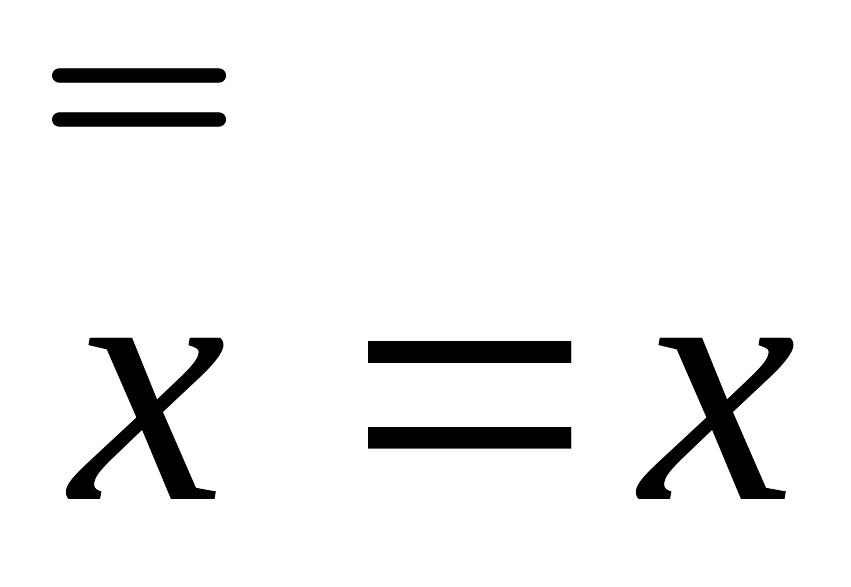 ;
;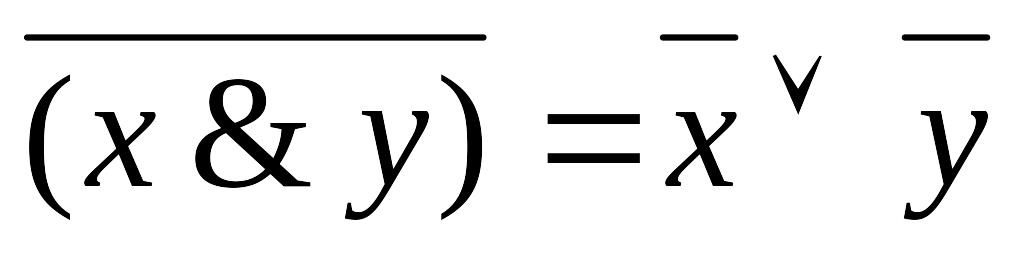 ;
;
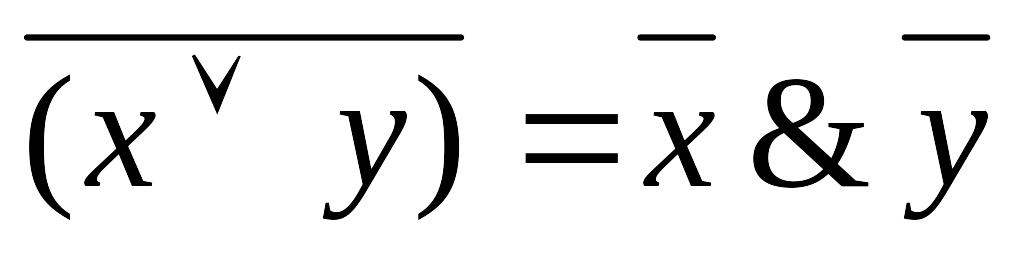 ;
;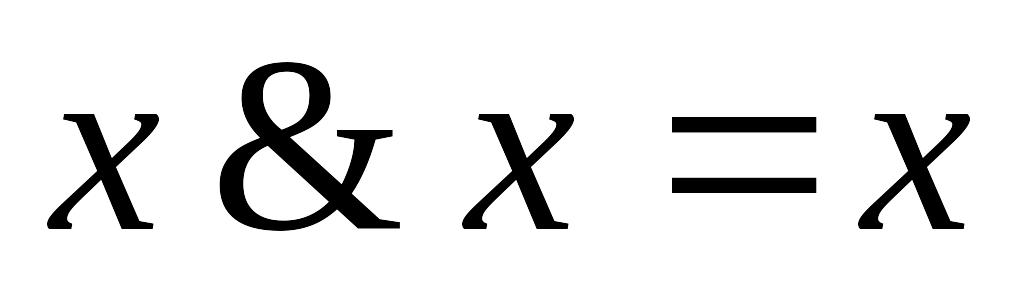 ;
;
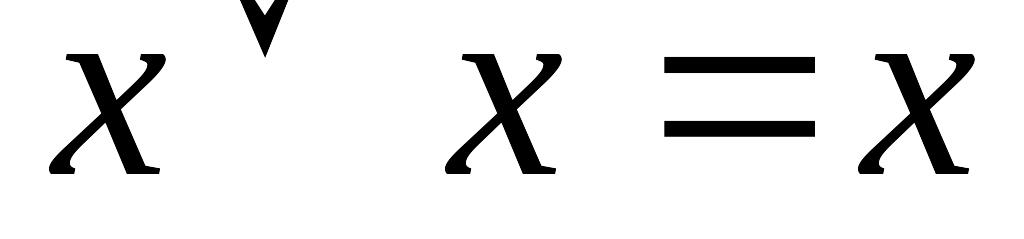 ;
;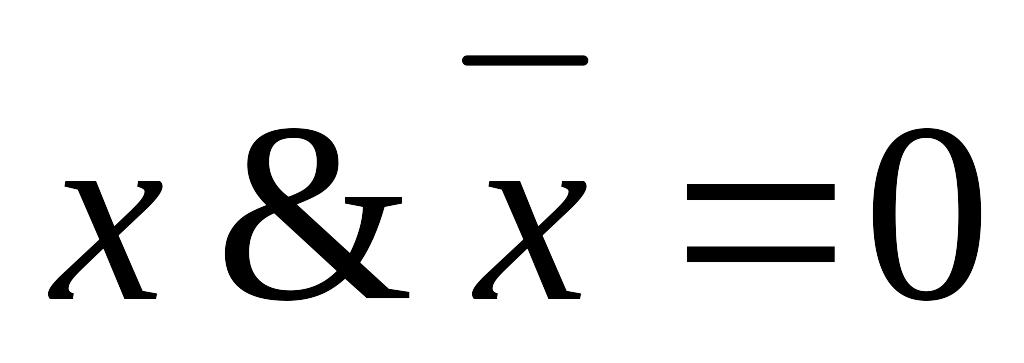 ;
;
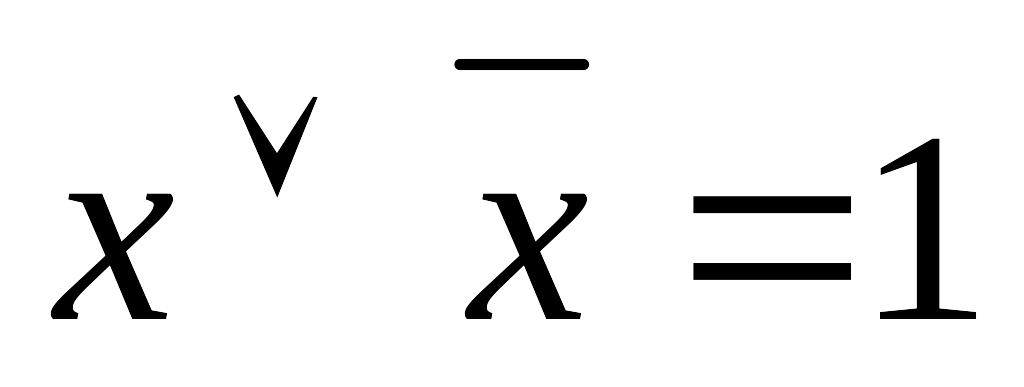 ;
;x & 0 = 0; x & 1 = x;
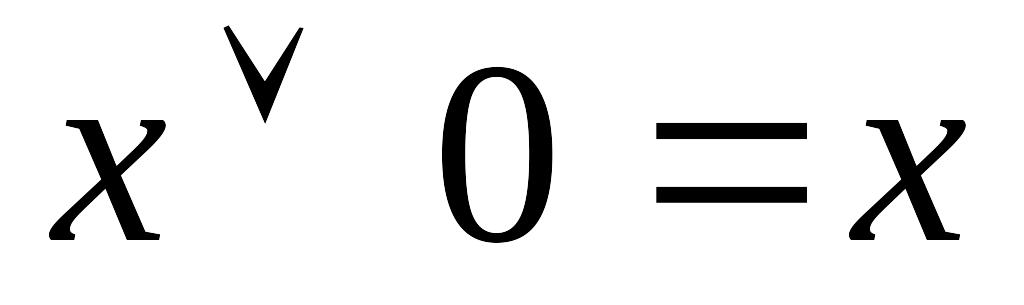 ;
;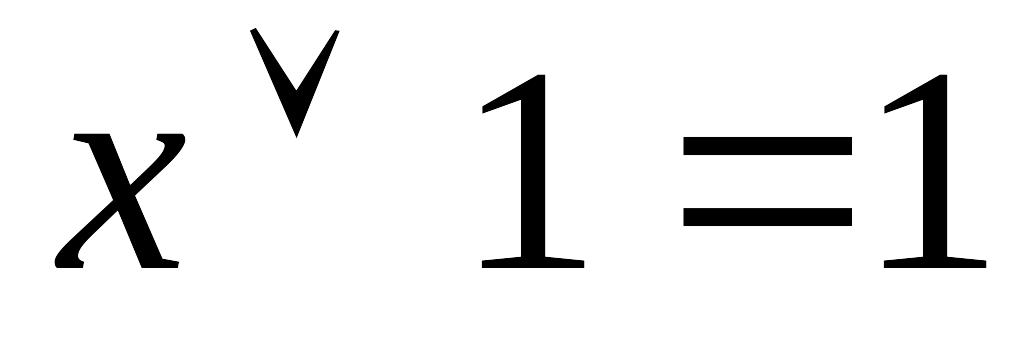 ;
;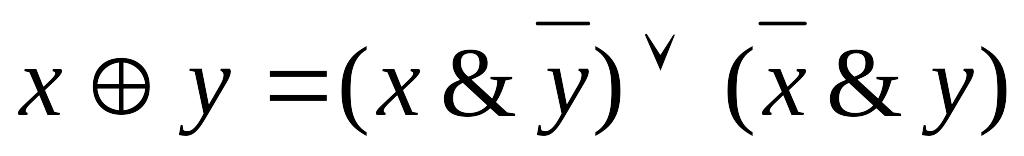 ;
; ;
;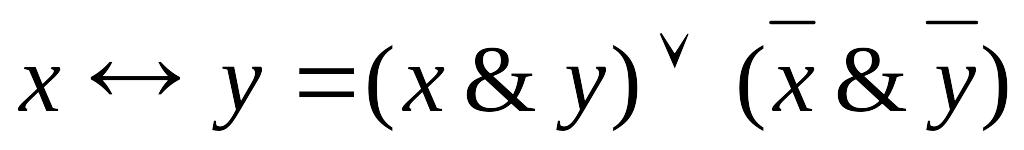 .
.
Примеры решения задач
Упростить выражение:
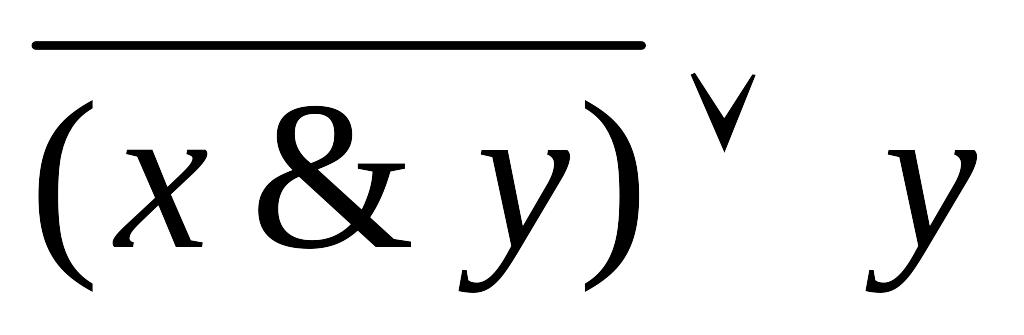 .
.
Решение.
![]()
Задачи для самостоятельного решения
Проверьте, справедливы ли следующие соотношения:
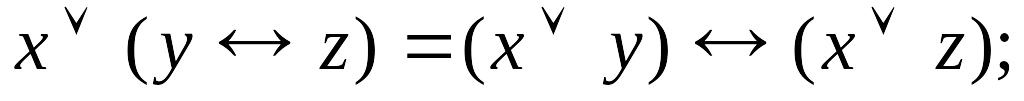


x (y & z) = (x y) & (x z)
Докажите равенства:
;
.
;
 .
.
Упростите выражение:
;
 ;
;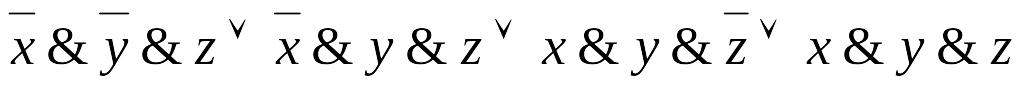 .
.
3.1.3.Двойственные функции
Симметрия элементов 0 и 1 в множестве B приводит к понятию двойственности.
Функция
![]() называется двойственной функцией
к функции f и обозначается f *.
Двойственными являются, например,
называется двойственной функцией
к функции f и обозначается f *.
Двойственными являются, например,
![]() и x ↔ y, задаваемые векторами (0,1,1,0)
и (1,0,0,1).
и x ↔ y, задаваемые векторами (0,1,1,0)
и (1,0,0,1).
Теорема. Функция, двойственная к двойственной функции f равна самой функции f.
Теорема. (Принцип двойственности). Функция, двойственная к суперпозиции функций, равна суперпозиции двойственных функций.
Функция f называется самодвойственной, если она равна своей двойственной: f=f*.
Например,
самодвойственны функции: х,
![]() .
.
А
функции: 0,
1,
![]() ,
,
![]() не являются самодвойственными.
не являются самодвойственными.
Примеры решения задач
Построить функцию, двойственную данной.
Решение.
Рассмотрим,
что происходит с таблицей двойственной
функции. Замена набора (x1,...,xn)
на
![]() соответствует «переворачиванию»
таблицы. Действительно, наборы (x1,...,xn)
и
расположены симметрично относительно
середины таблицы. Теперь остаётся
применить операцию отрицания к результату
функции, т.е. поменять 0 на 1 и 1 на 0. Т.о.
вектор значений функции, двойственной
к исходной, получается из вектора
исходной функции переворачиванием и
заменой 0 на 1, а 1 на 0.
соответствует «переворачиванию»
таблицы. Действительно, наборы (x1,...,xn)
и
расположены симметрично относительно
середины таблицы. Теперь остаётся
применить операцию отрицания к результату
функции, т.е. поменять 0 на 1 и 1 на 0. Т.о.
вектор значений функции, двойственной
к исходной, получается из вектора
исходной функции переворачиванием и
заменой 0 на 1, а 1 на 0.
Является ли функция f(x, y, z)=(0,0,0,1,0,1,1,1) самодвойственной?
-
Решение. Действуем по следующему алгоритму:
1. Строим в одной таблице функции f(x, y, z),
 и
и
 .
.2. Убедимся, что на одинаковых наборах f = f*.
В данном примере, как видно из таблицы, функция является самодвойственной.
x
y
z
f
0
0
0
0
1
0
0
0
1
0
1
0
0
1
0
0
1
0
0
1
1
1
0
1
1
0
0
0
1
0
1
0
1
1
0
1
1
1
0
1
0
1
1
1
1
1
0
1
