Методические указания к решению задач № 2, 3

Эти задачи относятся к неразветвлённым и разветвленным цепям переменного тока. Перед их решением изучите материал темы, ознакомьтесь с методикой построения векторных диаграмм и разберите решение примеров 2,3 в данных методических указаниях.

Пример 2. Неразветвленная цепь переменного тока содержит катушку с активным сопротивлением R_к = 3 Ом и индуктивным x_L = 12 Ом, активное сопротивление R = 5 Ом и конденсатор с сопротивлением х_С = 6 Ом (рисунок 9). К цепи приложено напряжение U = 100 В (действующее значение).

Определить:

1. полное сопротивление цепи;

2. ток;

3. коэффициент мощности;

4. активную, реактивную и полную мощности;

5. напряжение на каждом сопротивлении.

Начертить в масштабе векторную диаграмму цепи.

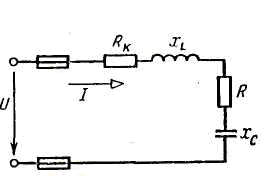
Рисунок 9. Схема цепи для примера 2

Решение:

1. Определяем полное сопротивление цепи:

Z = √R_к + R)² + (X_L – X_С)² = √(3 + 5)² +(12 – 6)² = 10 Ом;

2. Определяем ток цепи

I = U / Z = 100 / 10 = 10 А;

3. Находим коэффициент мощности цепи. Во избежание потери знака угла (косинус – функция четная) определяем

sin φ = (X_L – X_С) / Z = (12 – 6) / 10 = 0,6; φ = 36^о50'.

По таблицам Брадиса определяем коэффициент мощности

cos φ = cos 36^о50' = 0,8.

4. Определяем активную, реактивную и полную мощности цепи:

Р = U · I · cos φ = 100 · 10 · 0,8 = 800 Вт

или Р = I² · (R_K + R) = 10² · (3 + 5) = 800 Вт;

Q = I² · (x_L – х_С) =10² · (12 – 6) = 600 вар

или Q= U· I · sin φ =1000 · 10 · 0,6 = 600 вар;

S = U · I = 100· 10 = 1000 ВА

или S = I₂ · Z = 10² · 10 = 1000 ВА

и ли S = √Р² + Q² = √800² + 600² = 1000 ВА.

5. Определяем падения напряжения на сопротивлениях цепи:

U_Rк = 10 · 3 = 30 В;

U_L = I_ХL = 10 · 12 = 120 В;

U_R = I · R = 10 · 5 = 50 В;

U_С = I · Х_С = 10 · 6 = 60 В.

Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом по току: в 1 см – 2 А и масштабом по напряжению: в 1 см – 20 В. Построение векторной диаграммы (рисунок 10) начинаем с вектора тока, который откладываем по горизонтали в масштабе 10 А / 2 А = 5 см.

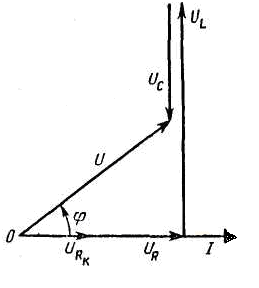
Рисунок 10. Векторная диаграмма для примера 2

Вдоль вектора тока откладываем векторы падений напряжений на активных сопротивлениях U_Rк и U_R в масштабе 30 В / 20 В = 1,5 см и 50 В / 20 В = 2,5 см.

Из конца вектора U_R откладываем в сторону опережения вектора тока на 90° вектор падения напряжения U_L на индуктивном сопро­тивлении длиной 120 В / 20 В = 6 см. Из конца вектора U_L откладываем в сторону отставания от вектора тока на 90° вектор падения напряжения на конденсаторе U_С длиной 60 В / 20 В = 3 см. Геометрическая сумма векторов U_Rк, U_R, U_L, U_С равна полному напря­жению, приложенному к цепи.

Пример 3. Цепь переменного тока состоит из двух ветвей, соединённых параллельно. Первая ветвь содержит катушку с активным R₁ = 12 Ом и индуктивным Х_L = 16 Ом сопротивлениями; во вторую ветвь включен конденсатор с емкостным сопротивлением х_С = 8 Ом и последовательно с ним активное сопротивление R₂ = 6 Ом. Активная мощность, потребляемая первой ветвью, P₁ = 48 Вт (рисунок 11).

Опре­делить:

1. токи в ветвях и в неразветвленной части цепи;

2. активные и реактивные мощности цепи;

3. напряжение, приложенное к цепи;

4. угол сдвига фаз между током в неразветвленной части цепи и на­пряжением. Начертить в масштабе векторную диаграмму цепи.

Решение:

1. Активная мощность P₁ теряется в активном сопротивлении R₁. Поэтому

P₁ = I₁² · R₁.

О тсюда I₁ = √ Р₁ / R₁ = √ 48 / 12 = 2 А.

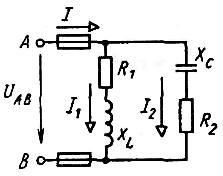
Рисунок 11. Схема цепи для примера 3

2. О пределяем напряжение, приложенное к цепи:

U_AB = I₁ · Z₁ = I₁ · √ R₁² + Х_L ² = 2 · √ 12² + 16² = 40 В.

3. О пределяем ток:

I₂ = U_AB / Z₂ = U_AB / √ R₂² + Х_С² = 40 / √ 62 + 82 = 4 А.

4. Находим активную и реактивную мощности, потребляемые цепью:

Р = I₁² · R₁ + I₂² · R₂ = 2² · 12 + 4² · 6 = 154 Вт;

Q = I₁² · Х_L – I₂² · Х_С = 2² · 16 – 4² · 8 = – 64 вар.

З нак «–» показывает, что преобладает реактивная мощность емкост­ного характера. Полная мощность, потребляемая цепью:

S = √ Р² + Q² = √ 154² + 64² = 166,8 ВА.

5. Определяем ток в неразветвленной части цепи:

I = S / U_AB = 166,8 / 40 = 4,17 А.

6. Угол сдвига фаз во всей цепи находим через sin φ во избежание потери знака угла:

sin φ = Q / S = – 64 / 166,8 = – 0,384; φ = – 22°35'.

Знак «–» подчеркивает, что ток цепи опережает напряжение U_AB.

Для построения векторной диаграммы определяем углы сдвига фаз в ветвях:

s in φ₁ = Х_L / Z₁ = 16 / √ 12² + 16² = 0,8; φ₁ = 53°10';

sin φ₂ = Х_С / Z₂ = – 8 / √ 6² + 8² = – 0,8; φ₂ = – 53°10'.

Задаемся масштабом по току: в 1 см – 1 А и напряжению: в 1 см – 5 В. Построение начинаем с вектора напряжения (рисунок 12). Под углом φ₁ к нему в сторону отставания откладываем в масштабе век­тор тока I₁; под углом φ₁ в сторону опережения – вектор тока I₂. Гео­метрическая сумма этих токов равна току в неразветвленной части цели.