Глава 1

ОСНОВНЫЕ ФАКТЫ

57

4% на любой длине волны, практически поглощает всю лз чистую энергию, достигающую его поверхности. Далее он проявляет любо­пытство по поводу сложной формы кривой спектрального коэффи­циента отражения светло-коричневого образца; ему интересно узнать, что эта кривая содержит информацию о том, что светло-коричневый цвет образца обусловлен наличием в нем по меньшей мере трех пигментов – красного, ответственного эа максимум поглощения при длине волны 550 нм; оранжевого, поглощающего

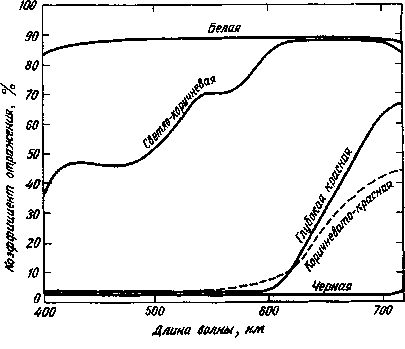
Рис. 1.11. Спектральные кривые коэффициента отражения для пяти предпо­лагаемых типов пластмасс белого, светло-коричневого, коричневато-красного, глубокого красного и черного цветов.

Приводимые кривые не соответствуют точно кривым отражения пластмасс, окрашенных реальными красителями, а вычерчены произвольно с целью проиллюстрировать рас­сказ об изготовителе радиоприемников, пытающемся закупить пластмассовые корпуса.

наиболее сильно вблизи длины волны 470 нм, и белого, максимум поглощения которого находится в ультрафиолетовой области (т. е. при длине волны, меньшей 400 нм). Но наибольшее внимание изготовителя привлекает к себе разница между кривыми, описы­вающими глубокий красный цвет образца, который он хочет воспроизвести, и коричневато-красный цвет (прерывистая линия) неприемлемого для него образца.

Изучая рис. 1.11, изготовитель радиоприемников уже пришел к некоторым правильным обобщениям. Он отметил, что белый образец (самый светлый из пяти) отличается также самым высо­ким коэффициентом отражения и что черный образец (самый тем­ный) отражает меньше всех остальных. Более того, светло-корич-

невый образец, цвет которого значительно светлее, чем у обоих красных образцов, отражает свет в любом участке спектра сильнее красных образцов. Очевидно, что коэффициент отражения неко­торым общим образом взаимосвязан со светлотой воспринимаемого глазом цвета. Чем выше процент света, отражаемого образцом,. тем светлее цвет, которым в нашем восприятии мы наделяем образец. /

Информация, содержащаяся в кривых рис. 1.11, позволяет сделать и другие обобщения. Существенная отличительная черта как белого, так и черного образцов заключается в том, что они отражают свет неизбирательно (неселективно), т. е. для них не су­ществует какого бы то ни было выделенного участка спектра,. в котором они, отражая, посылали бы в глаз наблюдателя намного больше энергии излучения, чем в других участках. В результате эти образцы имеют в нашем восприятии нейтральный или серова­тый цвет. Образцы светло-коричневого, коричневато-красного и глубокого красного цвета образуют цветовую последователь­ность возрастающей насыщенности, т. е. они все более отличаются от любого серого цвета. Можно отметить, что соответствующие кривые спектрального коэффициента отражения обладают все большей крутизной и, следовательно, для образцов в том порядке, в котором они перечислены, характерна возрастающая селектив­ность отражения света. Глубокий красный цвет образца очень сходен с цветом излучения участка спектра, примыкающего к длинноволновой границе видимого диапазона. В то же время цвет светло-коричневого образца хотя и несколько напоминает цвет' излучения участка спектра вблизи 585 нм, но по цветовому тону представляет собой очень бледное отбеленное подобие цвета этого излучения. Эти сравнения помогают прийти к общему правилу, что цветовой тон воспринимаемого цвета объекта соответствует цветовому тону излучения того участка спектра, в котором объект наиболее сильно отражает свет, а насыщенность воспринимаемого цвета соответствует степени селективности отражения, т. е. кру­тизне кривой спектрального коэффициента отражения.

Изготовитель теперь может понять, почему выбранный им вна­чале глубокий красный цвет воспринимался более насыщенным: кривая, описывающая спектральное изменение коэффициента отражения соответствующего образца, имеет большую крутизну. Однако, когда он пытается применить сделанный им обобщающий вывод о светлоте цвета к выяснению того, почему цвет коричневато-красного образца воспринимается как более светлый по сравнению с глубоким красным цветом, он осознает, что его обобщение имеет лишь качественный характер. Ибо в некоторых участках спектра образец глубокого красного цвета отражает свет во много раз больше коричневато-красного образца. Необходимо, чтобы спект­ральная область между 550 и 660 нм, в которой отражение второго

58 ГЛАВА 1

образца сильнее, чем у первого, обеспечивала бы больший вклад в светлоту, чем область, примыкающая к длинноволновому концу видимого спектра, в которой указанное соотношение между коэф­фициентами отражения изменяется на противоположное. Теперь впервые изготовитель ощущает необходимость в надежной инфор­мации психофизического характера. Он нуждается в основе для коммерческой спецификации, которая гарантировала бы, что поку­патель его изделий воспримет цвет пластмассового корпуса ни слишком светлым, ни слишком темным, ни слишком желтоватым, ни слишком синеватым и сероватым. Он понимает, что нужен метод, который помог бы предсказать, соответствует ли цвет одного образца цвету другого. Он извлек уже достаточный опыт, чтобы предполагать, что подобный метод должен быть основан на каком-то способе усреднения кривых спектрального коэффициента отра­жения каждого образца, но вклад различных участков спектра в получаемое среднее значение должен соответствовать характеру восприятия покупателем цвета изделия.

Изготовитель испытывает чувство удовлетворения, когда узна­ет, что такой метод действительно существует. В самом деле, имеет­ся метод, широко распространенный в промышленной практике цветового контроля и известный под названием метода измерения цвета МКО. Эта международная организация рекомендует основ­ные стандарты и процедуры, касающиеся всех аспектов света, освещения и осветительной техники, включая колориметрию (измерение цвета).

Используя метод МКО, изготовитель находит, что он должен знать спектральное распределение потока излучения, испускаемого источником, освещающим образцы. Выяснив зто, он должен при усреднении кривой спектрального отражения каждого образца использовать три взвешивающие функции (нередко называемые весовыми). Их именуют функциями сложения цветов, и они харак­теризуют цветовосприятие среднего наблюдателя с нормальным цветовым зрением.

При решении той частной проблемы, которой занят изготови­тель радиоприемников, применение метода МКО предсказывает, что два образца и в самом деле будут восприниматься неодинако­выми по цвету. Разумеется, изготовителя сразу же интересует воз­можность предсказания величины цветового различия (рассогла­сования цветов) и получения конкретных данных о том, будет ли цвет одного образца восприниматься более серым или более насыщенным, более красным, зеленым, синим или желтым, более светлым или более темным и тому подобное по сравнению с цветом другого образца. Сделать такие количественные предсказания довольно трудно, но и для этих целей были разработаны методы, с помощью которых изготовитель может узнать количественно выраженные с разумной степенью точности величину и направле-

ОСНОВНЫЕ ФАКТЫ 59

ние воспринимаемого различия в цвете двух образцов. Эти методы основаны на результатах многочисленных лабораторных экспе­риментов по выяснению визуального цветоразличения.

Предположим теперь, что изготовитель радиоприемников, и в самом деле, определил величину и направление воспринимае­мого различия в цвете двух образцов. Он испытывает озабоченность по поводу того, окажется ли такое различие приемлемым или хотя бы терпимым для его потребителей. Он спрашивает: «Может ли наука о цвете помочь мне в этом отношении и дать мне метод предсказания максимального отличия от исходно выбранного цвета, при котором мои изделия все еще будут раскупаться?». К сожалению, наука о цвете не может оказать ему сколько-нибудь значительной помощи при решении этой проблемы. Проблема предсказания приемлемости цветового различия в противополож­ность проблеме восприятия того же самого различия связана с оценкой параметров, которые часто выходят за пределы воз­можностей научного исследования. Она зависит от таких ненауч­ных вопросов, как сорт окрашиваемого материала и характер его предполагаемого или предвидимого конечного использования, технические трудности и издержки его производства, желания и мечты покупателя, заказывающего этот материал, и многих дру­гих факторов.

Прежде чем мы приступим к подробному изложению системы определения цвета МКО, оценке цветовых различий и условий, предъявляемых к цветовым допускам, рассмотрим еще некоторые из основных фактов, связанных с цветовым зрением и, следова­тельно, лежащих в основе цветовых измерений.

УРАВНИВАНИЕ ПО ЦВЕТУ

Если наблюдатель с нормальным цветовым зрением попытается изменить цвет какой-либо детали, попадающей в центр поля зре­ния, так, чтобы он был одинаков с цветом соседней детали, он в ко­нечном счете обнаружит, что должен располагать тремя независи­мыми средствами регулирования. Допустим, что он использует красную, желтую и синюю краски, обычно имеющиеся под рукой. Тогда, смешивая во всевозможных пропорциях две из них, он может добиться равенства цветов лишь в редких случаях. Даже получение коричневого цвета требует добавления синей краски к смеси красной и желтой. В цветовом многообразии, получае­мом смешениями трех красок, легко найти цвет, одинаковый с лю­бым заданным цветом, но исходных красок должно быть ни в коем случае не менее трех. Те же самые соображения применимы к крас­ному анилиновому, желтому и голубому красителям, используе­мым в цветной фотографии, литографии и цветной печати. Анало­гично, если наблюдатель пытается уравнять по цвету пятно света

60 ГЛАВА 1

на белом экране, освещая соседний с ним участок несколькими световыми пучками различного цвета, он в общем случае придет к выводу, что либо ему потребуются три таких цветовых стимула определенного спектрального состава, либо (если одновременно-смешиваются лишь два цветовых стимула) не только интенсивно­сти обоих стимулов, но и спектральный состав, по крайней мере одного из них, должны быть регулируемыми. То же правило приме­нимо к смешиванию цветов с помощью вращающегося и разделенно­го на отдельные разноокрашенные сектора диска; необходимо и достаточно разделить диск на четыре сектора, что дает три неза­висимых способа регулировки. Нормальное цветовое зрение трех­мерно!

Мы несколько раз указывали на трехмерную природу нормаль­ного цветового зрения. Мы подчеркивали, что для осуществления такого зрения в сетчатке должны присутствовать светочувстви­тельные пигменты или сочетания светофильтр-пигмент по меньшей мере трех различных типов. Далее, для интерпретации кривой спектрального хода коэффициента отражения образца, измеренно­го на спектрофотометре, и осуществления таким образом цветового измерения необходимо иметь три взвешивающие функции, или функции сложения цветов. И наконец, описание цветового вос­приятия требует трех переменных, таких как светлота, цветовой тон и насыщенность. Рассмотрение различных способов, с помощью которых один из центральных участков нашего поля зрения может быть уравнен по цвету с соседним участком, вновь указывает на трехмерность нормального цветового зрения, однако мы долж­ны проанализировать, что же в каждом отдельном случае проис­ходит с цветовым стимулом на его пути от источника света к сет­чатке глаза.

СЛОЖЕНИЕ ЦВЕТОВЫХ СТИМУЛОВ

Один из наиболее прямых методов изучения того, каким обра­зом наши глаза дают нам возможность воспринимать цвет, состоит в сложении световых потоков или, более точно, в сложении цве­товых стимулов. Сначала направим световой пучок (например, от лампы накаливания) так, чтобы он создавал освещенный уча­сток на белом экране. Энергия излучения отражается от этого уча­стка и преломляется частицами пигмента, окрашивающего экран. Отраженная энергия имеет такое пространственное распределение, что наблюдатель может видеть освещенный участок одинаково хорошо из многих различных положений относительно экрана. В любом из этих положений лишь малая доля отраженного потока излучения попадает в глаз и становится цветовым стимулом. Поскольку частицы белого пигмента действуют на энергию излу­чения какой-либо одной длины волны видимого спектра примерно

ОСНОВНЫЕ ФАКТЫ 61

-так же, как и на излучения другой длины волны (рис. 1.11), спек­тральный состав цветового стимула весьма близок к спектральному составу потока излучения, падающего на экран. Наблюдатель сразу же улавливает значение этой физически сложной ситуации. Он видит белый экран и на нем пятно желтого цвета. Более точно,

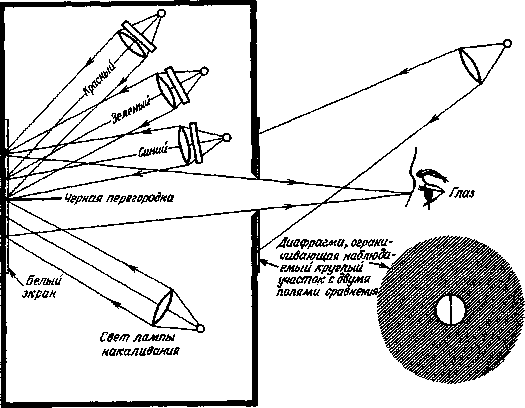
Рис. 1.12. Схематическое изображение устройства для демонстрации адди­тивного смешения цветов.

Это простое устройство помогает понять принцип трехмерной колориметрии. Справа внизу показано изображение поля зрения, как оно воспринимается наблюдателем. Левая половина внутреннего круга (одно из полей сравнения) порождает в глазу цветовой сти­мул, обусловленный излучением лампы накаливания; правая его половина (второе поле сравнения) порождает смесь красного, зеленого и синего стимулов, возникающих в результате отражения белым экраном трех излучений отдельных источников. Окру­жающее поле закрыто редуцирующим экраном, который можно оставить темным или освещать излучением наружного источника, который располагается сбоку от наблю­дателя.

это пятно имеет слабонасыщенный желтый цвет легкого краснова­того оттенка. Наблюдатель прекрасно осознает, что воспринимае­мый им цвет – цвет не экрана, а освещающего его излучения.

Затем направим на соседний участок экрана три световых потока, резко различающихся по цвету. Пусть их цвета будут, например, красным, зеленым и синим, как показано на рис. 1.12. Белые частицы пигмента экрана, как и прежде, диффузно отра­жают энергию излучения каждого из трех потоков практически

62 ГЛАВА 1

неселективно. Цветовой стимул, попадающий в глаз наблюдателя, представляет собой сумму отдельных стимулов, которые воздей­ствовали бы на глаз от каждого из трех перечисленных световых потоков, если бы источники двух других были отключены. При этом спектральный состав сочетания трех цветовых стимулов есть результат простого сложения трех отдельных стимулов, что можно проверить измерениями на спектрорадиометре. Наблюдатель видит второе пятно окрашенным в красный, зеленый, синий или какой-нибудь промежуточный цвет в зависимости от относительных интенсивностей потоков, испускаемых источниками красного, зеленого и синего света. И в этом случае он воспринимает цвет как принадлежность освещающего излучения, а не экрана, который, если его наблюдать, сам по себе воспринимается как белый. Дело упрощается, если неосвещенные участки экрана закрыты с помо­щью черной диафрагмы; тогда наблюдатель видит пятна просто как самосветящиеся участки поверхности. Этот прием называется редуцированием (сведением) цвета к изолированно воспринимае­мому (апертурному) цвету, а диафрагму называют редуцирующим экраном.

С помощью установки подобного типа мы можем выполнять некоторые весьма фундаментальные как качественные, так и коли­чественные эксперименты, относящиеся к цветовому зрению. Во-первых, мы можем установить, нельзя ли воспроизвести желтый цвет, или желтый стимул, смешивая стимулы, порождаемые красным, зеленым и синим излучениями. Исследуя эту возмож­ность, получим утвердительный ответ и найдем, что воспроизве­дение возможно при определенном соотношении интенсивностей трех излучений (количественно преобладающим должно быть красное, несколько менее интенсивным – зеленое и еще менее интенсивным – синее). Далее обнаружим, что воспринимаемые цвета любого цветового тона могут быть воспроизведены подобным смешением красного, зеленого и синего цветовых стимулов. Отклю­чая синий стимул и меняя соотношения красного и зеленого в сме­си, мы сможем воспроизвести последовательность цветов, вклю­чающую желтый, воспринимаемый нами как чистый, без какой-либо примеси красноватого или зеленоватого оттенков. Отключая зеленый стимул и меняя соотношение красного и синего, мы полу­чим последовательность пурпурных цветов, включающую в одина­ковой степени красноватый и синеватый оттенки. И наконец, отключая красный стимул, мы сможем воспроизвести последова­тельность зеленовато-синих цветов, включающую оттенок голубого цвета, в равной степени синеватый и зеленоватый. При одновре­менном воздействии на сетчатку всех трех стимулов возникают ощу­щения цветов, воспринимаемых менее насыщенными, чем пере­численные граничные цвета. Существует даже небольшая область таких соотношений красного, зеленого и синего стимулов, смеси

ОСНОВНЫЕ ФАКТЫ____________ 63

которых дают цвета столь низкой насыщенности, что их можно считать не имеющими никакого определенного цветового тона. Такие цвета называют ахроматическими, или нейтральными.

Дальнейшее исследование показывает, что не все цвета, кото­рые могут восприниматься от самосветящейся поверхности, можно уравнять каким-либо сочетанием красного, зеленого и синего сти­мулов. Некоторые воспринимаются чересчур яркими для уравни­вания. Но мы устанавливаем, что это – сравнительно простое ограничение, связанное с количественными характеристиками используемых потоков излучения. Мы в состоянии преодолеть его, применяя в соответствующих проекционных устройствах более мощные лампы, или повышая напряжение, питающее лампы, или концентрируя больший поток на данной площадке с помощью более мощных линз. Однако, что более важно, некоторые стимулы воспринимаются слишком насыщенными, чтобы их можно было уравнять по цвету, сохраняя неизменной нашу методику. Напри­мер, если участок, освещенный лампой накаливания и используе­мый как образец для сравнения, покрыть желтым желатиновым фильтром или желтым стеклянным светофильтром, наподобие выпу­скаемых для сигнализации уличного движения, либо желтым жид­ким светофильтром типа раствора хромистого калия, получаемый желтый цвет может оказаться насыщенным настолько, что его нельзя уравнять, даже отключив вовсе поток излучения синего цвета. О цветах, воспроизводимых смешением выбранных красно­го, зеленого и синего стимулов, говорят как о цветовом охвате системы. Цвета, которые мы не в состоянии уравнять при выбран­ных для смешения стимулах, находятся за пределами этого охвата.

Можно увеличить цветовой охват трехкомпонентных смесей, выбирая в качестве трех исходных стимулов цвета излучений опре­деленных участков самого видимого спектра. Но эксперименты такого типа, проводившиеся на протяжении последних 250 лет, показали, что не существует набора трех стимулов, смешение которых способно уравнять все другие стимулы. Значительные совокупности чистых спектральных цветов и цветов, близких к спектральным, всегда остаются вне цветового охвата любых трех стимулов.

Очевидно, что результаты этого простого эксперимента вновь заставляют нас обратиться к изучению некоторых фундаменталь­ных свойств глаза. Обычно эти результаты интерпретируют как свидетельство того, что кривые спектральных чувствительностеи фотопигментов глаза перекрываются. Иными словами, излучение почти всех участков видимого спектра возбуждает более чем один пигмент, и поэтому всегда более чем одна из трех независимых рецепторных систем участвует в механизме цветовосприятия. Если бы при подобном подходе удалось обнаружить участки спектра, излучения которых возбуждают только одну рецепторную систе-

454 ГЛАВА 1

ivry и не затрагивают двух других, тогда и только тогда мы могли бы ожидать, что сумеем воспроизводить все цвета смешением трех таких чистых спектральных стимулов.

Постоянство зрительного уравнивания цвета. Самосветящиеся участки поверхности, наблюдаемые нами в поле зрения, охарак­теризованном на рис. 1.12, имеют цвета, которые мы можем опи--сать в терминах яркости, цветового тона и насыщенности. Мы используем здесь термин «яркость» вместо «светлота», чтобы под­черкнуть, что мы воспринимаем излучение от освещенных площа­док, а не от пространственных объектов. Такое терминологическое различение нельзя считать существенным, но оно зачастую удобно, если нужно указать тип цветовосприятия при заданных условиях наблюдения: воспринимается ли цвет самосветящегося предмета (цвет излучения, цвет источника освещения) или цвет несамосве­тящегося объекта.

Когда наше восприятие цвета относится к первому типу, субъ­ективное ощущение яркости заключено в пределах от очень туск­лого (темного) до очень яркого (слепящего). Восприятие цвета несамосветящегося объекта дает ощущение светлоты (от черного до белого), при этом объекты воспринимаются как непрозрачные но отношению к другим объектам.

В эксперименте, проиллюстрированном на рис. 1.12, мы можем изменить тип восприятия цвета поля зрения, освещая переднюю поверхность редуцирующего экрана (теперь уже белого) от источ­ника, расположенного сбоку от наблюдателя. Такое расположе­ние обеспечивает падение излучения этого источника на ту часть белого экрана, которая не видна наблюдателю сквозь отверстие ^в редуцирующем экране, и наоборот – гарантирует, что оно не будет освещать поле зрения. Когда яркость редуцирующего экрана сравняется с яркостью излучения, наблюдаемого через отверстие, тип цветовосприятия меняется. Мы воспринимаем цвета, видимые через отверстия, уже не как цвета излучения (именуемые также цветами, не локализованными по глубине, или цветами в отверстии), а как цвета несамосветящихся объектов. При этом изменении типа цветовосприятия нам кажется, что отвер­стие исчезло, и на его месте мы видим два плоских окрашенных полукруга, воспринимаемых, как цветная бумага, наклеенная на редуцирующий экран. При этом мы можем заметить резкие изменения в яркости и цветности (цветовом тоне и насыщенности) цветов. Например, если при темном редуцирующем экране мы воспринимали через отверстие достаточно насыщенный оранжевый цвет, то при ярко освещенном редуцирующем экране, когда тип нашего цветовосприятия меняется, мы видим тот же участок поля зрения окрашенным в цвет, который можно было бы описать как темно-коричневый. Любопытно, что коричневый цвет можно уви-

ОСНОВНЫЕ ФАКТЫ 65

деть лишь при цветовосприятии второго типа (цвета объектов), но никогда – при восприятии цвета излучения (источника осве­щения). К другим цветам, воспринимаемым исключительно как цвета окрашенных объектов, относятся оливковый и черный.

Подобные эксперименты демонстрируют нам некоторые из поразительных особенностей восприятия цвета, в частности то, как резко наше восприятие может меняться при относительно незначительных изменениях условий наблюдения. Но эти экспе­рименты подтверждают также фундаментальный закон, известный как закон постоянства зрительного уравнивания цветов [374].

Предположим, что мы уравняли цвет стимула, порождаемого излучением лампы накаливания на левой половине круглого поля зрения (рис. 1.12), подобрав нужную для этого смесь красного, зеленого и синего стимулов на правой половине. Редуцирующий экран, окружающий эти два участка поля зрения, сначала затем­нен, затем мы освещаем его светом определенной яркости и цвет­ности и наблюдаем, как изменились цвета половинок поля. Нас уже не удивляет тот факт, что воспринимаемый цвет круглого поля изменился; но кроме этого мы замечаем, что цветовое равен­ство между двумя половинками этого поля сохраняется. Продол­жая эксперимент, мы установим, что почти при любом выборе яркости и цветности излучения, освещающего окружающую поле поверхность, равенство по цвету двух половинок поля остается неизменным.

Мы можем также направить взгляд на другие ярко окрашен­ные участки поверхности, с тем чтобы изменить состояние цветовой адаптации глаза. Но после этого – стоит посмотреть на первона­чальное поле, и мы установим, что цветовое равенство двух его половинок сохраняется.

Закон постоянства зрительного уравнивания справедлив не для всех возможных изменений условий наблюдения, но верен для всех тех изменений, которые важно учитывать на практике. Цве­товое равенство сохраняется при предварительной адаптации к излучениям умеренной и даже довольно высокой яркости, но оно нарушается, если глаз до наблюдения сравниваемых половинок поля подвергается воздействию излучения чрезвычайно высокой яркости [63, 703, 704].

Еще одно ограничение на справедливость этого закона возни­кает в том случае, когда изображения сравниваемых по цвету половинок поля выходят за пределы области сетчатки, в которой отсутствуют палочки (области желтого пятна), т. е. когда их угло­вые размеры превышают 2°. В этом случае уменьшение яркости двух половинок поля в одно и то же число раз может нарушить цветовое равенство: в цветовосприятие эффективно вмешивается палочковый механизм зрения и изменяет нашу оценку равенства цветов [381, 634, 661].

66 ГЛАВА 1

Законы Грассмана. В широком диапазоне условий наблюдения, в котором соблюдается закон постоянства зрительного уравнива­ния цветов, информация, которую можно выразить количественно, получая ее из экспериментов 'по смешению трех цветовых стиму­лов, была сведена Грассманом [196] в первые два закона.

1. Глаз может регистрировать лишь три вида различий (вари­аций) цвета (выражаемых, например, различием цветового тона, яркости и насыщенности).

2. Если в смеси трех цветовых стимулов один из них непре­рывно изменяется (в то время как два других остаются неизмен­ными), цвет смеси также изменяется непрерывно.

Грассман пошел дальше этих утверждений, сформулировав самый общий закон, подтверждающийся, как и первые два, экспе­риментально.

3. Смешение стимулов одного и того же цвета (т. е. одинакового цветового тона, одинаковой яркости и одинаковой насыщенности) дает идентичные по цвету результаты независимо от спектрального состава излучений, порождающих эти стимулы. Вся современная колориметрия основана на этом принципе. Он означает, что мы можем оперировать со стимулами, учитывая исключительно их цвет и не рассматривая их спектрального состава. Третий закон Грассмана влечет за собой следующие важные выводы.

а) Два стимула одного и того же цвета, порознь смешанные с двумя другими стимулами, цвета которых также совпадают, дают смеси одинакового цвета. Другими словами, если стимул а равен по цвету стимулу Ь, а стимул с – стимулу d, то цвет смеси (а + с) равен по цвету смеси (b + d). Это правило представляет собой эквивалент арифметической аксиомы: если равные величины скла­дываются с равными, то и результаты сложений равны.

б) Если стимулы одного и того же цвета вычитаются из смесей одинакового цвета, то остающиеся после вычитания цвета одина­ковы. Иначе говоря, если стимул а равен по цвету стимулу Ъ, а смесь стимула с уравнена по цвету со смесью d, то после вычи­тания а из смеси с цвет остатка будет тот же, что и после вычитания стимула Ъ из смеси d. Это правило также имеет эквивалент арифме­тической аксиомы: когда равные величины вычитаются из равных, результаты вычитаний равны между собой.

в) Если одна единица какого-либо стимула имеет тот же цвет, что и одна единица другого стимула, то цвет любого числа единиц (или любой доли единицы) первого стимула одинаков с цветом такого же числа единиц (или такой же доли единицы) второго. В дру­гой формулировке это можно выразить следующим образом: увеличение или уменьшение в одно и то же произвольное число раз потоков излучения, характеризующих величину двух стимулов одинакового цвета, но не нарушающего спектральных распре­делений этих потоков, не нарушает и цветового равенства, какими

ОСНОВНЫЕ ФАКТЫ 67

бы ни были спектральные распределения исходных стимулов. И для этого правила есть арифметический эквивалент: если одина­ковые величины умножаются (или делятся) на одно и то же число, результаты всегда одинаковы.

Следствия а), б) и в) иногда называют законами линейности при уравнивании цветов. В частности, следствия а) и б) утверждают, что при таком уравнивании имеет место аддитивность, а следствие в) выражает свойство пропорциональности.

Устройство, схематически изображенное на рис. 1.12, указы­вает на существование непосредственного, практического метода измерения цвета. Для любого цвета, входящего в цветовой охват системы трех стимулов, количества трех стимулов, необходимых для его воспроизведения, могут служить мерой этого цвета. Такие количества называют координатами данного цвета, а само устрой­ство, показанное на рис. 1.12, является по существу простейшим трехмерным колориметром.

Три стимула (красный, зеленый и синий), создаваемые тремя потоками излучения, носят названия инструментальных стимулов, опорных стимулов или основных цветов. Все перечисленные стиму­лы представляют собой, разумеется, радиометрические величины и как таковые могут быть выражены в радиометрических единицах (Вт). Иногда более удобным оказывается рассматривать стимулы как фотометрические величины и выражать их через фотометриче­ские единицы (например, кд-м^-2). Иногда удобным является выра­жение стимулов в произвольных психофизических терминах, таких, как отсчеты по шкалам красного, зеленого и синего цветов, отградуированных так, чтобы их смешение в одинаковых количе­ствах давало стимул, воспринимаемый как ахроматический (ней­тральный), например как дневной свет. В табл. А1 Приложения приведены основные радиометрические и фотометрические понятия и единицы.

Если бы мы захотели использовать визуальный колориметр, показанный на рис. 1.12, для испытания предложенных изготови­телю радиоприемников образцов пластмассы глубокого красного цвета и коричневато-красного, обусловленного красителем XG-12S, мы смогли бы легко сделать это, поместив сначала первый, а затем второй образец в одно из двух полей сравнивания, осве­щенное лампой накаливания, и найдя количества красного, зеле­ного и синего основных цветов, необходимые для уравнивания этих полей в первом и во втором случаях. Мы обнаружим, что наборы координат цветов двух образцов несколько отличаются друг от друга. Различные наборы цветовых координат характери­зуют образцы, когда они освещены лампой накаливания.

Описывая аддитивное смешение цветов и законы, связанные со зрительным уравниванием по цвету, мы достаточно вольно обра­щались с названиями цветов, таких, как красный, зеленый, синий,

68 ГЛАВА 1

нейтральный и т. п., основываясь на своем субъективном опыте восприятия при выполнении операций уравнивания по цвету. Такая практика совершенно обычна и очень полезна для начинаю­щих, когда им приходится знакомиться с понятием цветовых сти­мулов и проделывать самостоятельно действия по уравниванию цветов. Однако необходимо снова подчеркнуть, что наш опыт вос­приятия цвета может быть подвергнут радикальным изменениям, когда в экспериментах по смешению цветов изменяются усло­вия наблюдения. Тем не менее зрительно воспринимаемое равен­ство двух цветов, т. е. цветовое уравнивание двух стимулов раз­личного спектрального состава, остается в сущности неизменным при подобных изменениях. Именно зрительно воспринимаемое равенство цветов, а также законы, которыми оно определяется, интересуют нас в первую очередь; характеристика стимулов в тер­минах нашего субъективного восприятия (цветовой тон, насыщен­ность и светлота), или в иных терминах – на данной стадии изуче­ния основ науки о цвете не является существенной.

Переход от цветовых координат, которые определяют цвет смеси основных цветов в рассматриваемом выше эксперименте, к параметрам, определяющим цветовой тон, насыщенность и яр­кость, которые характеризуют наше субъективное цветовое вос­приятие цветового стимула, является сложным, и он тесно связан с условиями наблюдения, преобладающими во время экспери­мента. На первой стадии изложения, когда мы используем такие наименования цветов, как красный, зеленый, синий и другие, нам необходимо ясно осознавать приблизительность этих наиме­нований, которые могут иметь определенный смысл только в случае, если мы считаем, что на протяжении всего изложения условия наблюдения неизменны. Например, мы полагаем, что поверхность, окружающая рассматриваемые цветовые детали, создает при ярком дневном освещении стимул, близкий к тем стимулам, которые мы наблюдаем на полях сравнения при цветовых измерениях.

Трехкоординатное цветовое пространство. Законы цветового уравнивания, получаемые при аддитивном смешении световых потоков (цветовых стимулов) в том виде, как они сформулированы в законах Грассмана и следствиях из них, можно выразить про­стыми алгебраическими уравнениями и геометрически проиллю­стрировать в трехмерном пространстве, называемом также трех-координатным цветовым пространством. В этом пространстве каж­дый цвет, заданный тремя цветовыми координатами, представляется вектором. На рис. 1.13 в наклонной проекции изображена простая геометрическая интерпретация трехкоординатного цветового про­странства. Три основных цвета, красный (R), зеленый (G), синий (II), изображенные в виде прямых линий, расположенных под Некоторыми углами, являются осями системы координат. Если

ОСНОВНЫЕ ФАКТЫ 69

R, G, В есть цветовые координаты цвета S по отношению к выбран­ным основным цветам К, О, В, то цвет S есть вектор с проекциями R, G, В на соответствующие координатные оси. Взаимные распо­ложения трех осей основных цветов задаются более или менее произвольно. Эти оси в любом случае, как и оси любой косоуголь­ной декартовой системы координат, единственным возможным образом описывают трехмерное пространство при условии, что

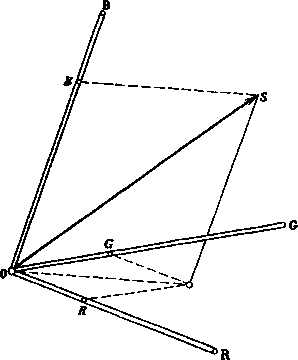
Рис. 1.13. Геометрическая интерпретация трехкоординатного цветового про­странства.

К, GiB представляют собой красный, зеленый и синий основные цвета соответственно. Цвет S представлен вектором в векторном пространстве R, G, В. Цветовые коорди­наты R, G, В являются проекциями вектора S на координатные оси R, G, В.

они исходят из одного центра (О) и не лежат в одной плоскости; это соответствует тому, что ни один из основных цветов не может быть получен какой-либо смесью (линейной комбинацией) двух других основных цветов. Масштабы на трех осях, т. е. единичные количества трех основных цветов, тоже можно выбрать произ­вольным образом, и только практические соображения побуждают нас сделать тот или иной целесообразный выбор. Один из целесо­образных выборов масштабов основан на том, что равные количе­ства К, G, В создают ахроматический цвет, соответствующий вектору (Ж), который пересекает единичную плоскость R + + G -f В = 1 в центральной точке N. Такой выбор масштаба про­иллюстрирован рис. 1.14. В устройстве для уравнивания цветов,

70

в котором поля сравнения окружены поверхностью, на которой создается стимул типа дневного света, цвет этой поверхности при­нимается за ахроматический цвет вектора N. В этом конкретном случае, когда оба поля сравнения и окружающее их поле уравнены

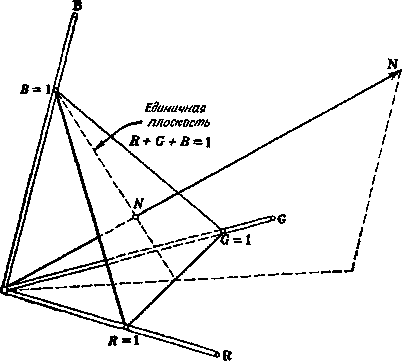
Рис. 1.14. Единичная плоскость и нейтральный цвет N в трехкоординатном цветовом пространстве, определенном выбором масштабов на осях R, G, В.

по цвету, цвета будут восприниматься как нейтральные ахрома­тические, или как белые (того или иного оттенка).

Алгебраическое выражение равенства между цветом S и соот­ветствующим образом подобранной смесью трех основных цветов R, G, В наиболее удобно записать в векторной форме:

8(Д, G, B) = RR + GG + BB. (1.2)

Если цвет S_x с координатами Д_1? G_v В_г смешивается со вторым цветом S₂ с координатами R₂, G₂, В₂, то образуется новый цвет S₀, координаты которого мы обозначим через R₀, G₀, B₀. В соответ­ствии с уравнением (1.2) получаем

S₀(R₀, G₀,B₀) = S_i(R_l,G_l,B_l) + S₂(R₂,G₂,B₂), (1.3)

или в более наглядной форме

S₀ (Д₀, G₀, B₀) = (R_iR + G₁G + B_iB) +

₊ (R₂R + G₂G + B₂B) =

= (R_i + R^R + (G_l + G₁)G + (B₁ + B_t)B. (1.4)

ОСНОВНЫЕ ФАКТЫ

71

Из этого следует, что координаты цвета смеси двух цветов пред­ставляют собой просто суммы соответствующих координат двух смешиваемых (или, как часто говорят, складываемых) цветов:

В₀= Ri + B₂,

G^Gt + Gt, (1.5)

Bo^Bt + B,.

Можно легко увидеть, что это правило верно и для смеси более чем двух цветов, и мы можем записать уравнения общего вида в форме

(1.6)

В нашей модели векторного пространства смешивание цветов соот­ветствует сложению векторов. Сложение двух векторов S₀ = = S_x + S₂ показано на рис. 1.15. На нем представлена единичная плоскость и на ней точки трех ее пересечений S_l7 S% и S₀ с тремя цветовыми векторами S_1? S_a и S₀. Поскольку S_1? S₂ и S₀ лежат в одной плоскости, три точки S_v S₂ и S₀ попадают на одну пря­мую – линию пересечения плоскости векторов (S_1; S₂, S₀) с еди­ничной плоскостью.

Единичная плоскость представляет для нас особый интерес. Важно отметить, что любой цветовой вектор S, или по крайней мере его продолжение, пересекает единичную плоскость в точке S. Эта точка пересечения S однозначно соответствует вектору S; поэтому ее можно использовать для определения вектора S во всех отношениях, кроме его длины, т. е. абсолютной величины. Мы называем S точкой цветности цвета S, или просто цветностью S. Участок единичной плоскости, заключенный внутри цветового охвата данной системы цветовых координат, обычно называют графиком цветности (или диаграммой цветности, или цветовым треугольником).

Термин «цветность» предполагает корреляцию с чувственно-воспринимаемой величиной, раньше называвшейся нами ощуще­ние цветности (она объединяет цветовой тон и насыщенность), которая всегда связана с данным стимулом, воспринятым при определенных условиях наблюдения. Как указывалось выше, такая корреляция может иметь смысл только в том случае, когда условия наблюдения заданы и неизменны. Только тогда мы имеем

72 ГЛАВА 1

право предполагать, что точка цветности S, расположенная вблизи центральной точки N графика цветности, характеризует стимул, который будет восприниматься как почти ахроматический. И толь­ко в этом случае точки цветности, расположенные вблизи углов графика цветности, можно считать соответствующими стимулам, порождающим в восприятии насыщенные красный, зеленый и синий цвета. Однако указанную связь между цветностью и ощущением

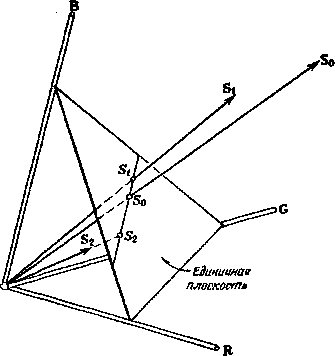
Рис. 1.15. Аддитивное смешение цветов S_x и S₂ дает цвет S₀. Геометрически S₀ представляет собой сумму векторов Sj и S₂. Все три вектора лежат в плоскости, которая пересекает единичную плоскость трехкоординатного цветового пространства по прямой линии Si, S₀, S₂. Точки S₀, Si, S₂ называются точками цвет­ности цветов So, Si, S₂ соответственно. Единичная плоскость носит название графика (или диаграммы) цветности.

цветности ни в коей мере нельзя рассматривать как простую. Решение задачи по определению ощущения цветности даже для одного стимула по его известной цветности связано со значитель­ными трудностями.

Чтобы установить положение точки S на графике цветности (и тем самым определить цветность вектора S), мы вводим коор­динаты цветности г, g, Ъ (рис. 1.16). Приизучении рис. 1.14 и 1.15 становится очевидным, что углы треугольника, изображенного на рис. 1.16, представляют собой пересечения осей основных цве­тов с единичной плоскостью. Они образуют систему отсчета на графике цветности, а их координаты цветности г, g, b задаются координатами (1, 0, 0), (0, 1, 0) и (0, 0, 1) для красного (В), зеленого (G) и синего (В) цветов соответственно. Координаты г,

ОСНОВНЫЕ ФАКТЫ 73

g, Ъ произвольной точки S определяются как кратчайшие расстоя­ния от S до трех сторон треугольника (G) (В), (В) (R) и (R) (G). Форма треугольника зависит от первоначально выбранной ориентации осей трех основных цветов в трехмерном пространстве. Мы сказали, что этот выбор может быть произвольным и, следо­вательно, треугольник любой формы может служить графиком цвет-

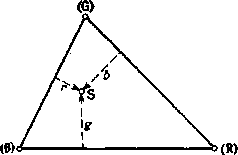
Рис. 1.16. График цветности (единичная плоскость) трехкоординатного цве­тового пространства.

Углы треугольника представляют собой точки цветностей (Я), (G), (В) основных цве­тов R, G, В, a S является точкой цветности цвета S с координатами цветности г, g, Ъ.

ности. У равностороннего треугольника есть преимущество сим­метричности по отношению ко всем трем основным цветам. Прямо­угольный треугольник, используемый в настоящее время в каче­стве диаграммы цветности, имеет то преимущество, что его легко. изобразить на обычной бумаге-миллиметровке.

Можно показать, что координаты цветности г, g, Ъ цвета S связаны с координатами этого цвета R, G, В следующими простыми соотношениями:

______R

B+G^B' откуда следует, что

r + g + b=i. (1.8)

Линейная зависимость между тремя координатами цветности, выра­женная в уравнении (1.8), показывает, что для однозначного опре­деления положения точки S на графике цветности необходимо и достаточно только двух координат (например, г и g); третья коор­дината (&) всегда может быть найдена простым сложением первых двух и вычитанием полученной суммы из единицы.

74

ОСНОВНЫЕ ФАКТЫ

75

Отрицательные координаты цвета – промежуточное звено в изложении. Определение цвета с помощью метода цветовых координат привело к возникновению нескольких полезных поня­тий, которые инженеры, физики, физиологи и психологи часто считали загадочными и головоломными. Одна из таких загадок заключается в появлении отрицательных чисел при определении цвета упомянутым методом. Если стимул, который при данных условиях наблюдения может восприниматься как бледный сине-зеленоватый, определяется цветовыми координатами R = 3, G = = 4, В = 4, мы легко можем понять, что это означает: для вос­произведения этого конкретного цвета нужно взять 3 единицы красного основного цвета, сложить (смешать) с ними 4 единицы зеленого основного цвета и добавить к полученной смеси 4 едини­цы синего основного цвета. Однако, если цветовые координаты насыщенного голубого цвета оказываются равными R = –3, G = 4, В = 4, это, по всей видимости, означает, что для воспроиз­ведения такого цвета требуется сложить 4 единицы синего основ­ного цвета и 4 единицы зеленого основного цвета, после чего из полученной смеси отнять три единицы красного основного цвета. Обычно при таком подходе возникает вопрос: «Как можно вычесть три единицы красного основного цвета из смеси, в которой его вообще нет?».

С отрицательными значениями цветовых координат неизбеж­но приходится сталкиваться в цветной фотографии и полиграфии, а также в цветном телевидении. Любой цвет, входящий в цветовой охват конкретных основных цветов системы (например, красного, зеленого и синего), может быть определен как сумма (смесь) поло­жительных количеств основных цветов. Цветовой охват ограничен в пространственной интерпретации тремя плоскостями (R = О, G = 0 и В = 0), которые пересекаются с единичной плоскостью ло прямым, образующим три стороны треугольника, показанного на рис. 1.15. Любой цвет S (R, G, В) входит в этот охват, если точка его цветности S (г, g, Ъ) расположена внутри цветового треугольника на единичной плоскости. Одна или две координаты цвета (и, следовательно, одна или две координаты цветности) становятся отрицательными, как только цвет S выходит за пре­делы цветового охвата системы. На рис. 1.17 изображены цвет S_1; заключенный внутри цветового охвата системы, и цвет S₂, нахо­дящийся вне его. Для определения цветов, выходящих за пределы цветового охвата системы, необходимо использовать отрицатель­ные значения цветовых координат. Например, в случае показан­ного на рис. 1.17 цвета S₂ значение координаты G отрицательно.

Такие цвета могут быть определены экспериментально, путем визуального уравнивания. Если цвет S имеет цветовые координаты R = –3, G = 4, 5 = 4, нам следует просто сложить (смешать) три единицы красного основного цвета R с этим исследуемым цве-

том S, а не добавлять R к смеси двух других основных цветов G и В. Мы найдем, что сумма S-J-3R уравнивает сочетание 4G + 4B, т. е.

S-f-3R = 4G + 4B. (1.9)

Согласно следствию б) из законов Грассмана, которое эквивалентно арифметической аксиоме: если равные величины вычитаются из

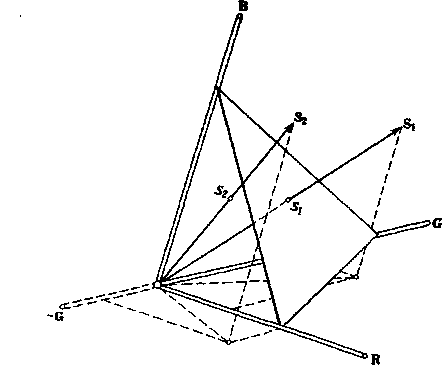
Рис. 1.17. Цветовой охват, получаемый смешением красного (R), зеленого (G) и синего (В) основных цветов.

S, является примером вдета, входящего в этот охват, a S, – примером цвета, выходя­щего за пределы цветового охвата системы.

равных, то и результаты вычитаний равны, мы можем записать S=-3R + 4G + 4B (1.10)

и идентифицировать величины (–3, 4, 4) с соответствующими цветовыми координатами R, G, В цвета S.

Преобразование основных цветов. Не существует двух в точ­ности одинаковых трехцветных колориметров. Некоторые из них изготовляются разными преднамеренно; другие, предназначенные для работы в одной и той же цветовой координатной системе (с одинаковыми наборами трех основных цветов), все же могут давать при их эксплуатации систематически различающиеся резуль­таты, Совершенно естественным поэтому является желание срав-

7G

ОСНОВНЫЕ ФАКТЫ

77

нить результаты, получаемые при цветовых измерениях с помощью одного трехцветного колориметра, с результатами, получаемыми при работе с другими. На основании третьего закона Грассмана, утверждающего, что цвета стимулов в их смесях можно рассмат­ривать совершенно независимо от их спектрального состава, мож­но выписать формулы, показывающие, как' рассчитать цветовые координаты любого цвета, которые мы получим при его измере­нии на одном трехцветном колориметре, по координатам того же самого цвета, определенным с помощью любого другого трехцвет­ного колориметра с известными основными цветами.

Если установлено, что координаты какого-либо цвета в системе первой триады основных цветов равны R, G, В, то координаты того же цвета X, У, Z в системе второй триады основных цветов будут определяться соотношениями

X = X_rR + X_gG + X_bB,

Y = Y_TR + Y_gG + Y_bB, (1.11)

Z = Z_rR + Z_gG + ZbB,

где X_r, Y_T, Z_r – количества основных цветов второй триады, сум­ма которых уравнивает цвет (R = 1, G = О, В – 0), X_g, Y_g, Z_g – количества тех же цветов, сумма которых уравнивает цвет (R = 0, G = 1, В = 0), и, наконец, Х_ъ, Y_b, Z_b – их количества, уравнивающие в сумме цвет (R = 0, G = 0, 5 = 1). Можно увидеть, что выписанные уравнения преобразования справедливы для любого из этих трех цветов. Действительно, взяв первый основ­ной цвет (R = 1, G = 0, В – 0) и приравнивая нулю В и G в уравнениях (1.11), a R положив равным 1, мы получим X = Х_г, Y = Y_r, Z = Z_r, как и предусматривалось условием. Значения цветовых координат Х_г, Х_е, . . ., Z_b, присутствующие в уравне­ниях (1.11), называются коэффициентами преобразования системы цветовых координат. Расположенные в виде таблицы чисел, на­считывающей три строки и три столбца, они образуют матрицу преобразования системы цветовых координат. Как только зада­ется матрица преобразования, так однозначным образом опреде­ляется и соотношение между двумя наборами основных цветов (X, Y, Z) и (R, G, В). Система уравнений (1.11) является есте­ственным следствием того положения, что можно взять любую сумму стимулов и рассматривать ее как отдельный стимул. Она справедлива для аддитивного смешения (сложения) любой состав­ляющей с двумя любыми другими составляющими при условии, что можно взять сумму составляющих смеси и затем обращаться с этой суммой так, как если бы она была отдельной составляющей в другой системе. Иными словами, она представляет собой закон сложения любых трех составляющих, выраженный в терминах двух различных наборов основных цветов.

Уравнения обратного преобразования для трехкомпонентных смесей находятся решением системы уравнений (1.11) относительно R, G, В. Мы получаем

Y_gZ_b – Y_bZ_g X_bZg – X_gZ_b it =-------д-------Х+-------д------- i +

XgY_b – X_hY_g

+------д------^z'

С -– ^Ъ^г – Y_rZb у | X_rZ_b– X_bZ_r у

+ ------д------Л

(1.12)

В=-

Y_TZg – Y_gZ_r XgZ_r – X_rZ_g

-----д------^х+------д–-

X_TYg–XgY_r

Л-----------А-------- ^Л.

Y +

где А называется определителем исходной матрицы преобразова­ния и записывается как

А = X_r (Y_gZ_b - Y_bZg) + X_g (Y_bZ_r - Y_rZ_b) -\-X_b(Y_rZ_g – Y_gZ_r).

(1.13)

Матрица преобразования, определяемая системой уравнений (1.12), называется обратной по отношению к исходной матрице систе­мы (1.11). Вид уравнений (1.12) более сложен, так как в них долж­но учитываться то обстоятельство, что вторая система цветовых координат может иметь три новых основных цвета, каждый из которых является трехкомпонентной смесью первого набора основ­ных цветов. Уравнения (1.12) полезны как отправной пункт для проектирования цветовоспроизводящих элементов устройств, в ко­торых должны вырабатываться три отдельных изображения каких-либо объектов с тем, чтобы последующее сложение трех изобра­жений давало цветную репродукцию этих объектов. Именно на этом принципе основаны некоторые системы цветной фотографии и цветного телевидения. Но о них мы будем говорить позднее.

Остается выписать уравнения преобразования для координат цветности. Очевидно, что переход от цветовых координат R, G, В к цветовым координатам X, Y, Z с использованием (1.11) будет сопровождаться переходом от координат цветности г, g, Ъ к коор­динатам цветности х, у, z. Новые координаты цветности х, у, z связаны с X, Y, Z уравнениями, аналогичными (1.7): х = XI(X + + Y + Z), у = Y/(X + Y + Z), z = Z/(X + Y + Z). Эти уравне­ния вместе с (1.11) и (1.7) приводят к следующим уравнениям пре-

78 ГЛАВА 1

образования координат цветности:

______________X_rr+X_gg+X_bb_____________

^Х - (X_r+Y_r+Z_r) r+(X_g+Y_g+Z_g) g+(X_b+Y_b+Z_b) Ъ '

_______________Y_rr+Y_gg+Ybb____________

^У (X_r+Y_r+Z_r)r+(X_g+Y_g+Z_g)g+(X_b-+Y_b+Z_b)b> ^(1Л4>

____________Z_Tr+Z_gg+Z_bb_____________

^Z ~ (X_r+Y_T+Z_T) r+(X_g+Y_g+Z_g) g+(X_b+Y_b+Z_b) b •

Соотношения r-\-g-\-b = l (1.8) и x-\-y-\-z = l дают воз­можность исключить Ъ из (1.14) и игнорировать уравнение для z. Сделав зто, мы можем записать

_____________(X_r-X_b)r+(X_g-X_b)g+X_b___________

^Х - [(X_r~Xb)+(Y_r-Y_b)+(Z_r~Z_b)\ _r+[(X_g-X_b)+(Y_g-Y_b)+ +(Z_g-Z_b)]g+[X_b+Y_b+Z_b),

(1.15)

_________(Y_r-Y_b)r+(Y_g-Y_b)g+Y_b

^У - [(X_r-X_b)+(Y_r-Y_b)+(Z_r-Z_b)} r+[(X_g-X_b)+ +_{Y_b-Y_b)+(Z_g-Z_b)] g₊[X_b+Y_b+Z_b).

Уравнения (1.15) можно выразить в обобщенном виде:

__ ^anr+ai2g+^ai3

a3ir+a₃₂g+a_S3 '

(1.16)

^а21Г+^а22£+^а23

а₃1Г+^а32£+^азз ' где коэффициенты a_ik (i, к = 1, 2, 3) представляют собой симво­лические обозначения соответствующих коэффициентов в (1.15), например а₁₂ = X_g – Х_ь. Отметим, что знаменатель в уравнениях для х та у одинаков. Это является характерной чертой всех подоб­ных преобразований, которые известны под общим наименованием проективных преобразований плоскости (в нашем случае – пло­скости графика цветности).

Итак, мы убедились, что линейному (или аффинному) преоб­разованию трехмерного цветового пространства соответствует проективное преобразование графика цветности. Справедливо также и обратное утверждение: проективному преобразованию графика цветности соответствует аффинное преобразование трех­мерного цветового пространства. Эти два типа преобразований весьма существенно отличаются один от другого типом искажений пространства или плоскости, соответственно с которыми может быть связано их существование. При проективном преобразовании (1.16) существует возможность обращения точек с конечными коор­динатами (г, Ъ) в точки (х, у), расположенные на бесконечности, и наоборот. За счет этого мы можем, производя простые операции,

ОСНОВНЫЕ ФАКТЫ 79

внести очень большие искажения в какой-либо данный график цветности. Из (1.16) легко видно, что за зто свойство проективных преобразований ответствен знаменатель я₃1^г + ^аз2# + ^азз = D, который при D = 0 является уравнением прямой линии в пло­скости (г, g). Соответствующая ей линия в плоскости (х, у) должна находиться в бесконечности (это явно следует из условия D = 0). Рассмотренное свойство проективных преобразований не присуще аффинным преобразованиям (1.11), поскольку в их выражении отсутствуют величины, записываемые в виде отноше­ния. Точки, расположенные на бесконечности, на ней же и остаются независимо от того, какие мы выберем коэффициенты преобразова­ния; соответственно точки, лежащие в конечных (финитных) областях пространства, после преобразования всегда будут рас­положены в таких же областях. Однако имеется свойство, общее для аффинных и проективных преобразований: при любом из них прямые линии переходят в прямые линии.

При изучении проективных преобразований были установле­ны многочисленные геометрические свойства графиков цветности [716]. Многие из этих геометрических свойств имеют непосредст­венное отношение к психофизическому понятию цвета и зачастую помогают уяснению его смысла. Примером может служить, часто кажущаяся озадачивающей интерпретация понятия точки цвет­ности, выходящей за пределы цветового охвата, ограниченного сторонами цветового треугольника (рис. 1.15). С помощью проек­тивных преобразований можно легко показать, что подобное рас­положение точки цветности не имеет никакого психофизического значения, пока речь идет о реальных цветах. Можно подобрать такие преобразования, которые превращают «внутренние» цвет­ности во «внешние», и наоборот. Можно определить условия, позво­ляющие заранее выяснять, сохранит ли данное проективное преоб­разование все «внутренние» точки в пределах цветового треуголь­ника [712].

В следующей главе этой книги (см. раздел о равноконтрастных графиках цветности) мы познакомимся с проективными преобра­зованиями, специально подбираемыми так, чтобы построить гра­фики цветности, на которых кратчайшее расстояние между двумя точками было бы прямо пропорционально воспринимаемому раз­личию в ощущении цветности с постоянным коэффициентом про­порциональности, независимо от расположения точек на графике.

Функции сложения цветов. В изложении проблемы зрительного цветового уравнивания мы подошли к этапу, на котором можем провести специальный эксперимент по такому уравниванию. Как мы увидим позднее, результаты этого эксперимента представ­ляют собой психофизические данные, которые могут служить осно­вой для построения теорий цветового зрения и создания практиче-

ОСНОВНЫЕ ФАКТЫ

81

ского метода измерения цвета. Цель нашего специального экспее римента заключается в определении функций сложения цветов для наблюдателя с нормальным цветовым зрением.

Мы опять прибегнем к помощи визуального колориметра, пока­занного на рис. 1.12. Однако на этот раз для нас удобнее будет использовать в этом колориметре монохроматические (спектраль­ные) цветовые стимулы. Монохроматический стимул представляет еобой поток излучения в очень узком интервале ЛЯ видимого диа­пазона; центр интервала (центральную длину волны) обозначим просто Я. Типичная ширина подобного интервала ЛЯ равна 5 нм; при этом, разумеется, нас интересуют все такие интервалы, кото­рые, будучи взятыми вместе, образуют непрерывный спектр в види­мом диапазоне длин волн излучения – примерно от 380 до 770 нм. Обычно монохроматический стимул именуют просто стимулом длины волны X, подразумевая, конечно, что эта длина волны явля­ется центральной в узком интервале длин волн ЛЯ,, взятом в пре­делах указанного непрерывного спектра.

С помощью монохроматора мы получаем стимул длины волны X. Монохроматор представляет собой оптическое устройство, раз­лагающее поток излучения (например, испускаемый лампой нака­ливания) в его спектр и дающее нам возможность выделить из этого спектра любой нужный нам узкий участок, излучение кото­рого пропускается выходной щелью монохроматора, образуя необходимый нам цветовой стимул длины волны X. Величина сти­мула измеряется, например, его энергетической яркостью, т. е. величиной потока излучения, испускаемого единицей площади (в нашем случае – площади выходной щели) в единицу телесного угла и в расчете на единичный интервал длин волн (Вт-см^-2-•ср^_1-нм^_1). Эта величина регулируется оптическим аттенюатором (ослабителем), помещенным у выходной щели монохроматора. Простым и эффективным оптическим аттенюатором является клино­образный нейтральный светофильтр с высоким коэффициентом пропускания на его тонком конце, непрерывно уменьшающимся при перемещении к толстому концу, где его значение мало. Пере­двигая клин вдоль выходной щели, мы меняем значение энерге­тической яркости стимула, уменьшая или увеличивая его. Надле­жащая калибровка этого так называемого фотометрического клина позволяет нам количественно точно оценивать ослабление исход­ного потока излучения из щели.

Для нашего визуального колориметра нам нужно четыре моно­хроматора: три – для получения трех основных стимулов системы цветовых координат и один – для создания испытательного сти­мула (тест-стимула). Монохроматоры устанавливаются вместо источников света, показанных на рис. 1.12; однако предусмат­ривается возможность перемещения их поодиночке с одной сто­роны цветового поля сравнения на другую. Нам сразу же станет

ясна необходимость этого конструктивного новшества, поскольку цвет монохроматического тест-стимула часто должен быть лишен насыщенности перед цветовым уравниванием двух половинок поля. Такое состояние тест-стимула достигается добавлением к нему соответствующего стимула одного из основных цветов, с тем чтобы мы могли уравнять цвет получившейся смеси цветом подходящей смеси двух оставшихся основных стимулов. Как было показано раньше, подобный перевод одной из цветовых координат с одного поля сравнения на другое делает эту коор­динату отрицательной.

После этих конструктивных изменений мы готовы к проведению запланированного эксперимента по уравниванию цветов. Основ­ные стимулы устанавливаются монохроматическими излучениями с длинами волн Яд = 700,0 нм для красного цвета (R), X_G = = 546,1 нм для зеленого (G) и Х_в = 435,8 нм для синего (В). Единицы основных цветов выбираются так, что их энергетиче­ские яркости относятся между собой примерно как L_R : L_G : L_B = =72,1 : 1,4 : 1,0. Этот выбор производится на основе вспомогатель­ного эксперимента, при котором цвет смеси единичных количеств основных цветов уравнивается с цветом равноэнергетического стимула. Равноэнергетический стимул можно представить себе как аддитивную смесь всех монохроматических стимулов, состав­ляющих непрерывный спектр от 380 до 770 нм, в котором каждый стимул имеет одну и ту же энергетическую яркость L₀xAX.

Набор стимулов с длиной волны Я, составляющих при сложе­нии равноэнергетический спектр, служит также тест-стимулом, и мы просмотрим эти стимулы один за другим, от X = 380 нм до X = 770 нм с интервалами ЛЯ = 5 нм. Общее число тест-стиму­лов равной энергетической яркости, каждый из которых испус­кается одним из четырех монохроматоров, составляет 79.

Производя реальное уравнивание цветов, мы вскоре обнару­жим, что нет никакой необходимости поддерживать каждый тест-стимул на постоянной энергетической яркости. Например, окажется желательным повысить энергетическую яркость вблизи концов видимого спектра, чтобы обеспечить более разумную величину стимула при функционировании только дневного зре­ния, т. е. зрения, обусловленного механизмом работы колбочек в сетчатке. Если мы знаем энергетическую яркость тест-стимула при цветовом уравнивании, то мы легко можем рассчитать коли­чества первичных цветов, которые будут уравнивать тест-стимул той же длины волны, но другой энергетической яркости. Чтобы сделать это, достаточно вспомнить следствие в) из законов Грасс мана. Пусть Ь^АХ – энергетическая яркость тест-стимула при уже совершенном цветовом уравнивании, a L_Q\AX – энергети­ческая яркость, при которой такого уравнивания еще необходимо достичь. Тогда количества основных цветов R (Я), G (Я), В (Я),

82

ОСНОВНЫЕ ФАКТЫ

83

т. е. цветовые координаты в первом случае, должны быть умно­жены на частное Ь_й^Ык1Ь%,Ык. В результате мы получим новые

Таблица 1.2

Функции сложения цветов r(>,), g (X,), 6 (Я), средние

для наблюдателей с нормальным цветовым зрением,

рассматривавших круглое поле с угловым размером в 2°.

Энергетические яркости монохроматических основных цветов

R (700,0 нм), G (546,1 нм), В (435,8 нм) относятся

приблизительно как L_R : L_G : L_B = 72,1 : 1,4 : 1,0 [101].

Тест- стилгул посто­янной знврввтичес/еой яркости на длине

Функции сложения цветов (.ординаты кривых сложения, или удельные координаты)

Волны \(нм)	г(\)	*(М	ЦК)
380	0.00003	-0.00001	0.00117
400	0.00030	-0.00014	0.01214
420	0.00211	-0.00110	0.11541
440	-0.00261	0.00149	0.31228
460	-0.02608	0.01485	0.29821
480	-0.04939	0.03914	0.14494
500	-0.07173	0.08536	0.04776
•520	-0.09264	0.17468	0.01221
540	-0.03152	0.21466	0.00146
560	0.09060	0.19702	-0.00130
580	0.24526	0.13610	-0.00108
600	0.34429	0.06246	-0.00049
620	0.29708	0.01828	-0.00015
640	0.15968	0.00334	-0.00003
660	0.05932	0.00037	0.00000
680	0.01687	о.ооооз	0.00000
700	0.00410	0.00000	0.00000
720	0.00105	0.00000	0.00000
740	0.00025	0.00000	0.00000
760	0.00006	0.00000	0.00000

цветовые координаты г (К), g (Я), Ъ (Я), которые и будут коорди­натами стимулов длины волны Я постоянной энергетической яркости L₀xAX.

Наконец, подчеркнем еще раз, что наблюдатель следит за двумя полями сравнения той формы, которая изображена на рис. 1.12. В глазу наблюдателя угловые размеры двух полей срав-

нения составляют 2°. Эта величина является максимальной при использовании для оценки цвета только области желтого пятна. Как указывалось раньше, цвет области, окружающей поля срав­нения, не сказывается на результатах уравнивания этих полей, и мы можем эту область оставить темной.

Типичные, хотя и весьма сжатые, данные по цветовому урав­ниванию при условиях, оговоренных выше и связанных с исполь­зованием трех фиксированных основных цветовых стимулов R (700,0 нм), G (546,1 нм) и В (435,8 нм), приведены в табл. 1.2.

В каждой строке табл. 1.2 для тест-стимула длины волны Я приведены измеренные координаты цвета г (Я), g (Я), Ъ (Я). Отме­тим, что во'многих случаях одна из координат цвета отрицательна, а это указывает на то, что цветовое уравнивание фактически достигается использованием одного из основных цветов для уменьшения насыщенности цвета тест-стимула. В других случаях одна или две координаты цвета могут равняться нулю, что указы­вает на возможность цветового уравнивания с использованием двух или одного основного цвета соответственно.

Удельные координаты г (Я), g (Я), Ъ (Я) монохроматических (спектральных) стимулов различных длин волн, но одной и той же энергетической яркости, взятые в совокупности, образуют, как их принято называть, функции сложения (или смешения) цветов по отношению к данным основным цветам R, С*, В. На рис. 1.18 приведены эти функции, вычерченные в виде кривых по значе­ниям, сведенным в табл. 1.2. Длины волн Я тест-стимулов и основ­ных цветов отложены по оси абсцисс, а цветовые координаты (при одной и той же энергетической яркости) тест-стимулов – по оси ординат. Как и следовало ожидать, эти функции являются непре­рывными и, более того, достаточно гладконепрерывными. У них есть положительные и отрицательные участки, переходы между которыми совершаются при значениях длин волн, соответствую­щих основным цветам.

Конкретные экспериментальные данные, приведенные выше, включают результаты, полученные Гилдом [205] и Райтом [702]. С помощью линейного преобразования они вывели функции сло­жения цветов х (К), у (Я), z (Я) для стандартного колориметриче­ского наблюдателя МКО 1931 г.

В то время как функции сложения цветов г (Я), g (Я), b (Я) относятся к реальным основным цветам (R при 700,0 нм, G – 546,1, В – 435,8 нм), функции сложения цветов х (Я), у (Я), z (Я) относятся к нереальным основным цветам X, Y, Z, т. е. физически не существующим. Нереальные основные цвета были выбраны так, чтобы облегчить колориметрические расчеты, связанные с функциями сложения цветов. Мы отмечали на рис. 1.18 и в табл. 1.2, что г (Я), g (Я), b (Я) обладают как положительными, так

6*

и отрицательными значениями, которые доставляют некоторые неудобства при численных колориметрических расчетах и пре­образованиях, с использованием функций сложения цветов.

ОСНОВНЫЕ ФАКТЫ

85

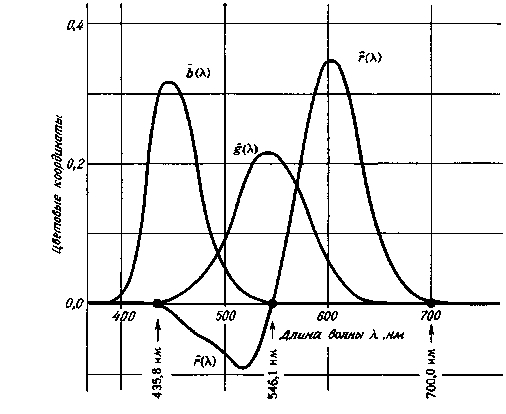
Рис. 1.18. Цветовые координаты г (Я), g (Я), Ъ (Я) спектрально чистых сти­мулов различной длины волны, но одинаковой энергетической яркости (при использовании в качестве основных цветов спектральных стимулов: R с дли­ной волны 700,0 нм, G – 546,1 и В – 435,8 нм). Единичные значения основных цветов выбраны так, что их энергетические яркости отно­сятся как L_R: Lq. L_b = 72,1 : 1,4 : 1,0. Этот набор из трех координат спектраль­ных цветов (удельных координат) г (%), g (Я), Ь (А,) называют также функциями сло­жения цветов по отношению к данному ряду основных цветов R, G, В. Следует огово­рить, что изображенные функции справедливы для среднего наблюдателя с нормальным цветовым зрением.

Конечно, эту нежелательную особенность функций сложения цветов г (Я), g (Я), Ъ (Я) нельзя обойти в визуальных эксперимен­тах, где необходимо использовать реальные цвета. Однако новые функции сложения, которые оказываются положительными в пре­делах всего видимого спектра, могут быть получены линейным преобразованием функций г (Я), g (Я) и b (Я). Имеется много таких линейных преобразований, из которых мы могли бы выбрать какое-то одно. Однако для всех из них характерно то обстоятель­ство, что основные цвета, к которым привязаны новые функции

сложения цветов, должны быть нереальными, и поэтому они являются лишь математическим вспомогательным средством.

МКО в 1931 г. выбрала одно конкретное линейное преобразо­вание для перехода от функций сложения цветов г (Я), g (Я), Ъ (Я) к стандартным функциям сложения х (Я), у (Я), z (Я) не только с целью сделать эти функции х (у), у (Я) и z (Я) положительными

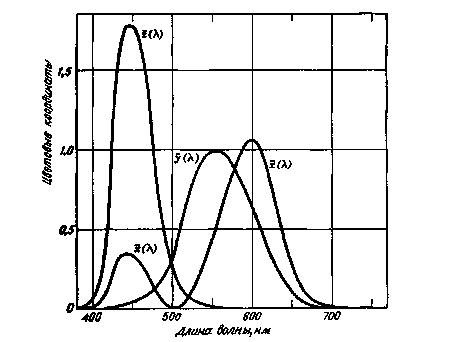
Рис. 1.19. Удельные координаты цвета г (Я), у (Я), z (Я), полученные линей­ным преобразованием из удельных координат цвета г (Я), g (Я), Ъ (Я), пока­занных на рис. 1.18.

Координаты ~х (X), ~у (J.),^-z (Я) выражают различные цвета через нереальные основные цвета X, Y, Z и определяют те свойства стандартного колориметрического наблюда­теля МКО 1931 г., от которых зависит правильность уравнивания цвета.

повсюду в видимом спектре, но и использовать их некоторые дру­гие свойства для колориметрических вычислений [314].

Подробно о выбранном линейном преобразовании можно про­читать в издании МКО 1971 г., а также в книге Вышецки и Стайлса [736], которая подытоживает экспериментальные работы Гилда [205] и Райта [702] и выражает их результаты через х (Я),

У (Я), 7 (Я).

Мы будем время от времени ссылаться на стандартные функ­ции сложения цветов МКО 1931 г. во многих последующих раз­делах настоящей книги. В частности, мы встретим эти функции ^в разделе о фундаментальных стандартах колориметрии.

На нынешней стадии нашего изложения нам придется доволь­ствоваться графическим изображением функций х (Я), у (Я), z (Я)

86 ГЛАВА 1

(рис. 1.19) и трехмерным цветовым пространством, построенным на основных цветах X, Y, Z (рис. 1.20 и 1.21).

На рис. 1.20 представлена геометрическая модель трехкоор-динатного цветового пространства, определяемого основными цве­тами X, Y, Z. Его единичную плоскость X + Y + Z = 1 назы­вают графиком цветности системы МКО 1931 г. Отметим, что

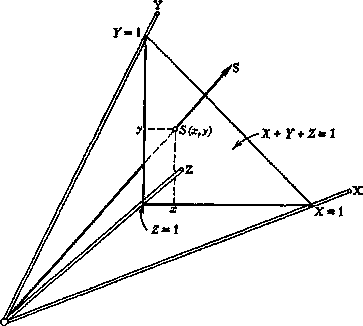
Рис. 1.20. Трехкоординатное цветовое пространство, построенное на основных цветах МКО 1931 г. X, Y, Z.

Ориентация.оеей основных цветов выбрана так, чтобы единичная плоскость (X + У + Z = = 1) в положительном квадранте давала прямоугольный треугольник, называемый графи­ком цветности. Цвет S пересекает единичную плоскость в точке S, именуемой точкой цветности; ее положение определяется координатами цветности х, у.

цветовой треугольник в этой системе является прямоугольным. Как и в трехкоординатном цветовом пространстве, построенном на основных цветах R, G, В (рис. 1.13–1.16), координаты цвет­ности х, у, z в системе X, Y, Z связаны с цветовыми координа­тами X, Y, Z простыми соотношениями:

^Х X+Y+Z'

– ^Y

^У~X+Y+Z»

_ Z

^{2 –} X+Y+Z с очевидным условием

x + y+z^l

ОСНОВНЫЕ ФАКТЫ 87

На рис. 1.20 показаны прямоугольные координаты цветности х, у, выбранные таким образом, чтобы определить точку цветности S цвета S.

На рис. 1.21 представлено то же самое трехкоординатное цве­товое пространство, определяемое основными цветами X, Y, Z. Однако на нем дополнительно показаны примеры цветов S (Я) монохроматических стимулов длин волн Я, причем Я, изменяясь,

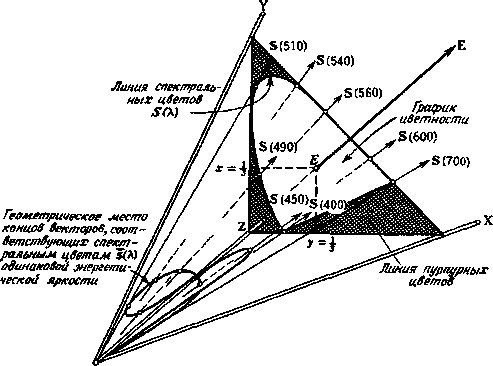
Рис. 1.21. Трехкоординатное цветовое пространство, построенное на основ­ных цветах МКО 1931 г. X, Y, Z.

Показаны график цветности (зс, у) и на нем линия пурпурных цветов. Кроме того, изо­бражена линия, являющаяся геометрическим местом точек конца всех векторов S (А,), спектральных цветов) стимулов длины волны X и постоянной энергетической яркости. Цвет Е, пересекающий график цветности в точке Е (х = у = 7„) представляет собой цвет равноэнергетического стимула.

принимает значения от 400 нм, что соответствует коротковолно­вому концу видимого спектра, до 700 нм (участок вблизи длин­новолнового конца этого спектра). Точки пересечения векторов йЗ (Я) с единичной плоскостью, взятые в совокупности, образуют линию, состоящую из прямой и кривой. Эту линию обычно назы­вают линией чистых спектральных цветов на графике цветности. Линия спектральных цветов начинается при значении длины вол­ны 400 нм и заканчивается при 700 нм. Точки цветности стимулов, которые мы можем получить, смешивая в различных пропорциях стимулы длин волн Я = 400 нм и Я = 700 нм, расположены на пря­мой линии, соединяющей точки цветности S (400) и S (700). Ее

88