Глава 2

нении (2.56). В самом деле, Семмельрот приводит соотношение

К« = 0,5754215 –0,658646. (2.57)

Значение V_a фона, являющееся функцией номинального зна­чения светлоты образца V_s, зависит, разумеется, от фона. Вот

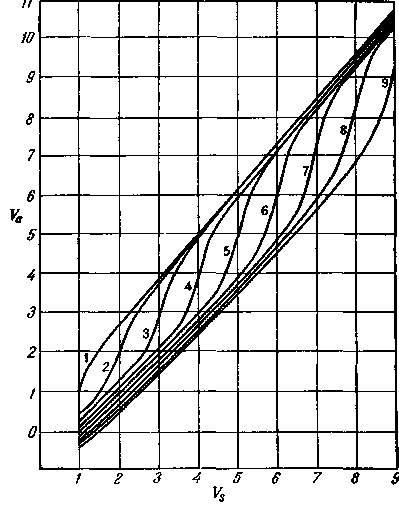
Рис. 2.73. Зависимость уточненных значений светлоты по Манселлу V_a от но­минальных значений светлоты по Манселлу V_a для фонов с номинальной свет­лотой по Манселлу 1/, 2/ . . . 9/ (данные представлены из таблицы Г598]).

почему на рис. 2.73 представлен ряд кривых, относящихся к каж­дому из девяти различных фонов. Каждый фон определен его номи­нальной светлотой по Манселлу, обозначенной на рис. 2.73 числами от 1 до 9. Единицы V_a выбраны такими, чтобы соответ­ствовать единицам, приблизительно равным светлоте (по Манселлу) относительно фона с изменяющимся коэффициентом яркости. Таким образом, мы отмечаем, что для V_s = 1, 2, 3, . . ., имеем У_а « 1, 2, 3, ... для соответствующих фонов 1, 2, 3, ....

СРЕДСТВА И МЕТОДЫ КОЛОРИМЕТРИИ

331

Ниже приведены примеры, иллюстрирующие использование рис. 2.73.

Пример 1. Различие светлоты двух образцов с V_s = 2 и V_s = 3 на фоне со светлотой 7/ приблизительно равняется AV_a = = 1,65 – 0,7 = 0,95. Соответствующее различие тех же образцов, рас­сматриваемых на фоне со светлотой 3/, равно AF_a = 3,0 – 1,2 = = 1,8. Это почти вдвое больше, чем для фона со светлотой 7/.

Пример 2. Образец со значением светлоты по Манселлу V_s = 3, рассматриваемый на фоне со светлотой 5/, имеет показатель свет­лоты V_a « 2. Такой же показатель светлоты V_s = 2 получается для образца со значением V_s = 2 на фоне с светлотой 2/.

Пример 3. Эффект волны явственно наблюдается в области, где V_s приблизительно соответствует светлоте фона; в этой области каждая кривая имеет точку перегиба. Например, при увеличении F_s на половину ступени от 5/ для фона 5/ V_a увеличивается на 1,35 ступени (6,35 – 5,0 = 1,35). Это более чем вдвое превышает увеличение, вызванное увеличением V_s от 8/ до 8,5/ при той же светлоте фона 5/ (9,9 – 9,4 = 0,5).

РАВНОКОНТРАСТНЫЕ ШКАЛЫ ЦВЕТНОСТИ

Ощущение цветности цветового восприятия определяется одно­временно цветовым тоном и насыщенностью при постоянной свет­лоте. В психологическом цветовом теле изменения в одном ощу­щении цветности представлены горизонтальными плоскостями постоянной яркости. Таким образом, равноконтрастная шкала цветности представляет собой двумерную последовательность цве­тов равной светлоты, каждый из которых воспринимается одина­ково отличающимся от своих ближайших соседей. Если в наличии имеется большое количество цветных образцов одинаковой свет­лоты, то можно отобрать образцы, следующие этому критерию на основе метода, представленного на рис. 2.67 этапами от а до ж. Хорошим приближением к такой равноконтрастной шкале является метод отбора образцов цветового тела в соответствии с правильной ромбоэдрической решеткой. Такой набор вскоре будет выпущен Американским оптическим обществом.

Создать такую двумерную последовательность равноконтра-стно распределенных цветов одной и той же светлоты можно по-другому, используя шкалы цветового тона и насыщенности по Манселлу. Как было показано ранее на рис. 2.59, они образуют полярную систему координат для каждой плоскости постоянной светлоты по Манселлу. Постоянная светлота по Манселлу не соот­ветствует постоянной светлоте, однако если мы примем, что эти два термина приблизительно одинаковы, то можно продолжить

332

СРЕДСТВА И МЕТОДЫ КОЛОРИМЕТРИИ

333

рассмотрение дальше. Все, что мы должны сделать, заключается в наложении па сетку полярных координат Манселла решетки из равносторонних треугольников (рис. 2.74). Такие решетки явля­ются плоскостями поперечных сечений правильной ромбоэдриче­ской решетки, которую мы ввели выше. В таком случае каждый узел треугольной решетки однозначно соответствует цвету в систе­ме Манселла и может быть записан с использованием обозначений Манселла. Такой отбор образцов в системе Манселла в соответствии

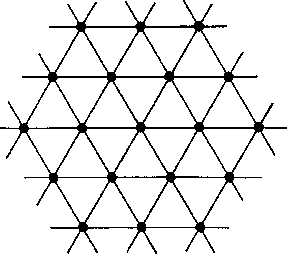
Рис. 2.74. Треугольная решетка для равноконтрастного шкалирования цвет­ности.

с решеткой был рассчитан Вышецким [711–713]. Результаты, полученные для цветов со значением светлоты по Манселлу 5/, представлены на рис. 2.75.

Подобные образцы решетки можно получить для других пло­скостей постоянной светлоты по Манселлу. Девять треугольных решеток, составленных определенным образом, образуют пра­вильную ромбоэдрическую решетку, полностью охватывающую пространство Манселла.

Конечно, равноконтрастное цветовое пространство, а тем самым и двумерную шкалу ощущения цветности равносветлых цветов можно получить только в случае эвклидовой геометрии цветового пространства. Если геометрия цветового пространства неэвкли­дова, любая шкала ощущения цветности в лучшем случае будет лишь приблизительно равноконтрастной.

Очевидно, что система Манселла, как, возможно, и любая дру­гая из существующих систем восприятия цвета, не является совер­шенно равноконтрастной. Однако работа комитета по равноконт-растным цветовым шкалам Американского оптического общества,

по-видимому, свидетельствует о возможности хорошей аппрокси­мации идеального равноконтрастного цветового пространства в эвклидовом пространстве.

Было предпринято несколько попыток найти путем нелиней­ного преобразования систему координат для стандартного коло­риметрического наблюдателя МКО 1931 г., которая по существу

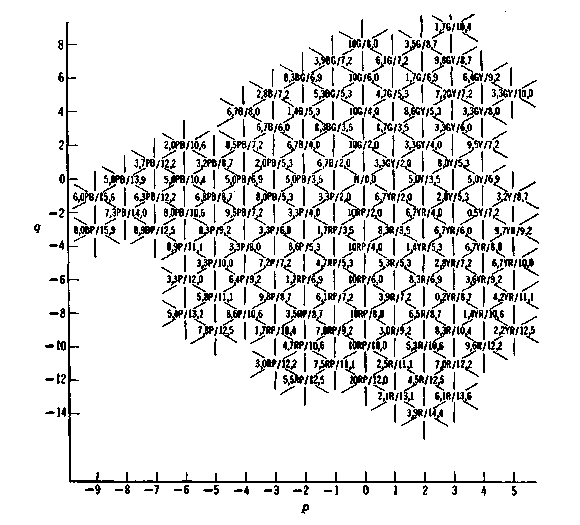
Рис. 2.75. Заполнение треугольной решетки цветами при светлоте по Манселлу

5/ [713]. Для каждого узла решетки с координатами (р, q) дано соответствующее обозначение.

приводила бы к такому же расположению ощущений цветности, как и в системе Манселла [7, 149, 151, 168, 180, 357, 442, 498, 576, 577, 647]. Многие из этих попыток привели к достаточно хорошим приближениям, но за счет довольно сложных формул нелинейного преобразования. По-видимому, сложным арифметическим рас­четом не обращаются к технологу по цвету, если существует более простой, но, возможно, несколько менее точный метод. Однако

334

нелинейное преобразование, известное как «график Адамса», является одним из наиболее широко используемых для оценки зна­чимости цветовых измерений и будет рассмотрено в дальнейшем в связи с расчетом цветовых различий [7]. Другим хорошим при­ближением к расположению цветов в пространстве Манселла являет­ся система координат, включающая функцию кубического корня, которая также довольно проста [180]. Позже у нас будет возмож­ность детально обсудить эту систему и ее дальнейшие разработки.

Равноконтрастные цветовые графики. Другой способ построе­ния равноконтрастной двумерной шкалы цветности состоит в том, чтобы использовать надежные данные по распределению цветности вместо данных, получаемых с помощью шкал цветового тона и насы­щенности в системе Манселла.

Джадд нашел, что данные такого рода, полученные до 1935 г., находятся в хорошем соответствии (с точностью до множителя, равного 2) с их представлением на плоском графике [317]. Он пред­ложил проективное преобразование типа

-с^У-

(2.58)

У

«31^ – аз22/ + ^а3з' ^сЛ^х-1-С22У + С23 ^с31-£-т-сз22/ + сзз'

которое переводит цветовой график (х, у) МКО 1931 г. в новый цветовой график (х', у').

Новый график называется равноконтрастным цветовым графи­ком (UCS), потому что он получен в соответствии с данными по рас­пределению цветов с приблизительно одинаковым расстоянием между парами точек, соответствующих цветностям, найденным экспериментально, и визуально одинаково отличающихся друг от друга.

Равноконтрастный цветовой график Джадда в течение многих лет использовался в качестве руководства по расположению цвет­ности ряда важных с практической точки зрения цветов и стан­дартных образцов цвета [61, 351, 434,435]. В дальнейшем он исполь­зовался для определения изотемпературных линий при расчете коррелированной цветовой температуры нечерных тел [351]. Изо-температурные линии представляют собой кратчайшие расстояния между линией черного тела и точкой, представляющей цветность рассматриваемого нечерного тела. Равноконтрастный цветовой график использовался также при разработке метода определения цветопередающих свойств источников света и при определении белизны бумаги [53, 319, 320].

Важность равноконтрастного цветового графика охотно приз­нается, она побудила других исследователей заняться его улучше­нием или разработкой новых равноконтрастных графиков, осно-

СРЕДСТВА II МЕТОДЫ КОЛОРИМЕТРИИ

335

ванных на различных экспериментальных данных [57, 150, 266, 266, 397, 482, 643]. Стало привычным определять равноконтра­стный цветовой график как проективное преобразование цветового графика (х, у) МКО 1931 г. или цветового графика (х₁₀, у₁₀) МКО 1964 г. Другими словами, равноконтрастные цветовые графики часто определяются системой уравнений, например вышеприведен­ной системой уравнений (2.58). Однако, как будет показано ниже, термин равноконтрастный цветовой график применим не только к проективным преобразованиям, но и к другим нелинейным пре­образованиям.

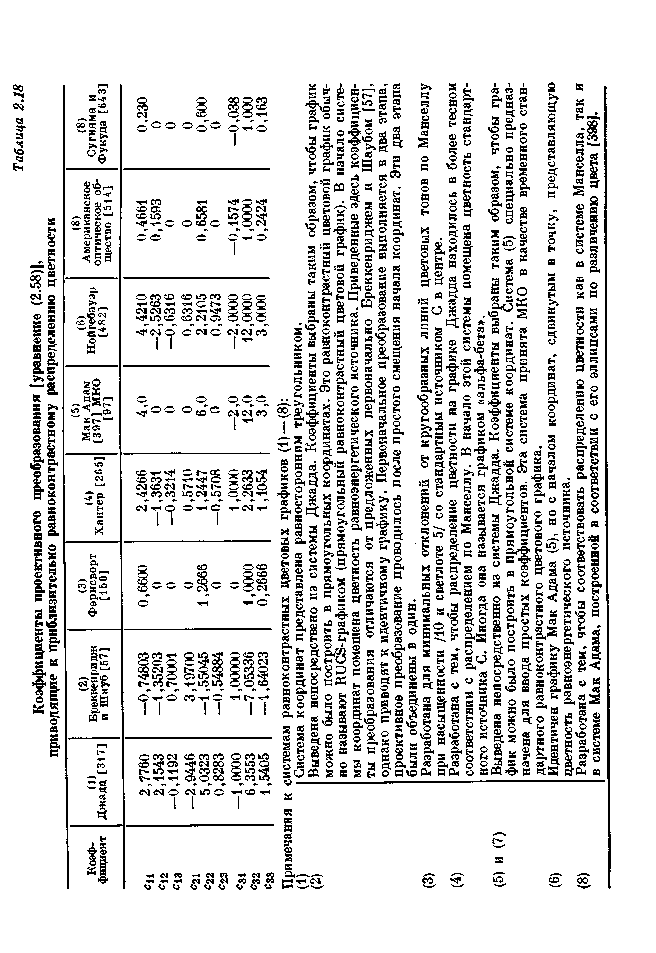
Равноконтрастные цветовые графики, основанные на различ­ных проективных преобразованиях, характеризуются различными наборами коэффициентов преобразования (с_п, с₁₂, . . ., с₃₃). В табл. 2.18 представлены коэффициенты для ряда равноконтра­стных цветовых графиков, приведенных различными авторами. Осо­бое внимание следует уделить равноконтрастному цветовому гра­фику, разработанному Мак Адамом [397]. В 1960 г. этот график был принят МКО в качестве временного стандартного равноконтра­стного цветового графика [101]. Его называют равноконтрастным цветовым графиком МКО 1960 г. В соответствии с табл. 2.18 уравнения преобразования, приводящие к этому графику, запи­сываются в виде

4х

-2я + 12^3 •

Этот же график определяется уравнениями

4Х

-15У-6У

-3Z'

(2.59)

(2.60)

' X – 15r+3Z'

где вместо координат цветности х, у уравнения (2.59) использованы координаты цвета А, Y, Z.

На рис. 2.76 представлен равноконтрастный цветовой график МКО 1960 г., определяемый уравнением (2.59) или (2.60). На рис. 2.77 показан тот же график с линиями постоянных значений х и у, наложенными на прямоугольную сетку координат и, v. Они иллюстрируют искажение сетки х, у, необходимое для полу­чения более равноконтрастного распределения цветности.

Значительным успехом МКО является тот факт, что после мно­голетних дискуссий удалось достичь соглашения по вопросу стан­дартного равноконтрастного цветового графика. Трудность при достижении соглашения заключалась не только в том, что каждый

СРЕДСТВА И МЕТОДЫ КОЛОРИМЕТРИИ

337

стремился выдвинуть используемую им систему, но и в том, что на результаты существенное влияние оказывали условия наблю­дения. Принятие равноконтрастного цветового графика Мак Адама не было связано с его преимуществом по сравнению с дру­гими графиками. Действительно, в то время, когда этот график был выбран в качестве стандартного, только предполагалось, что он

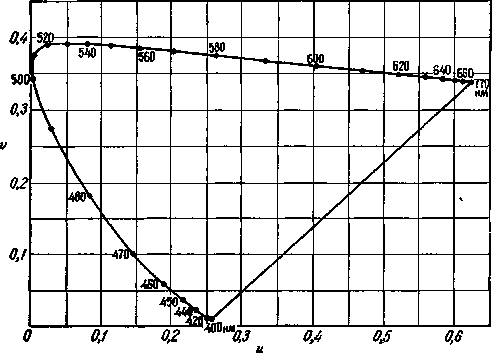
Рис. 2.76. Равноконтрастный цветовой график МКО 1960 г., представляющий проективное преобразование цветового графика х, у МКО 1931 г.

дает распределение цветности примерно такое же равноконтра-стное, как и в других системах, другими словами, график Мак Адама рассматривался в качестве характерного графика подобного типа. Возможно, что решающим фактором, определившим оконча­тельный выбор этого графика, явился тот факт, что коэффициенты преобразования, приводившие к этому графику, являются про­стыми целыми числами и таким образом удобными в применении [уравнение (2.59)].

В одной из своих последних теоретических работ Джадд и Ионемура [354] нашли тесную взаимосвязь между вторым этапом теории зрения Мюллера и равноконтрастным цветовым графиком МКО 1960 г. Рассматривая нормальное зрение как комбинацию протанопии и тританопии, в соответствии со вторым этапом теории Мюллера можно разработать более общую меру воспринимаемой величины различия в цветности по сравнению с длиной линии,

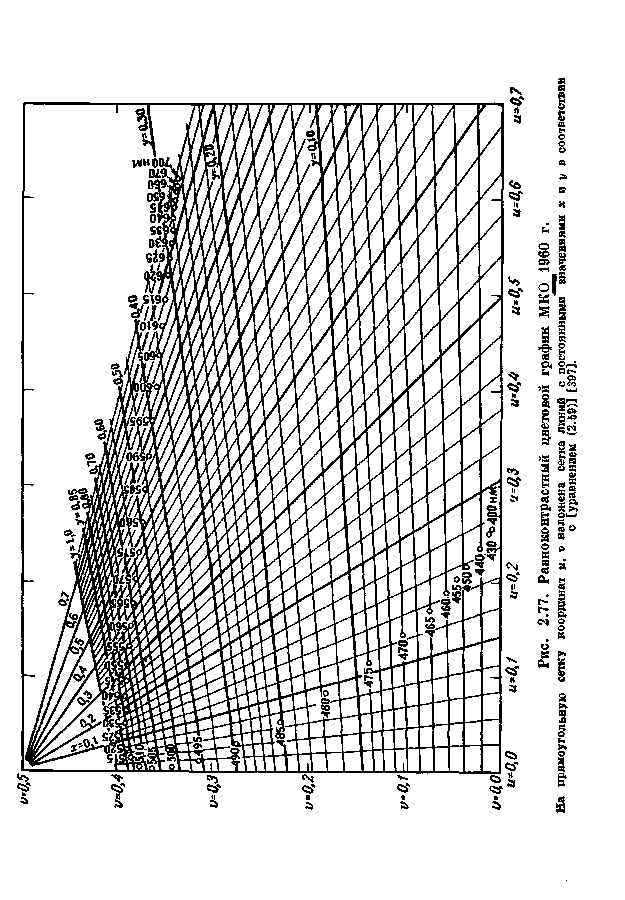
СРЕДСТВА И МЕТОДЫ КОЛОРИМЕТРИИ 339

соединяющей две точки цветности. Общей мерой, предложенной Джаддом и Ионемурой, является квадратный корень из суммы квадратов углов, образованных прямыми цветностеи, не различае­мых протанопами (рис. 2.14, а) и тританопами (рис. 2.14, Ь).

С помощью этой меры дается количественное объяснение экспери­ментальных данных по различению длины волны не только для про-танопов и тританопов, но и для наблюдателей с нормальным зрением.

Возможность восприятия различий в цветности лучше всего иллюстрируется экспериментальными данными, полученными Райтом [705, 706], Мак Адамом [398] и Стайлсом [626].

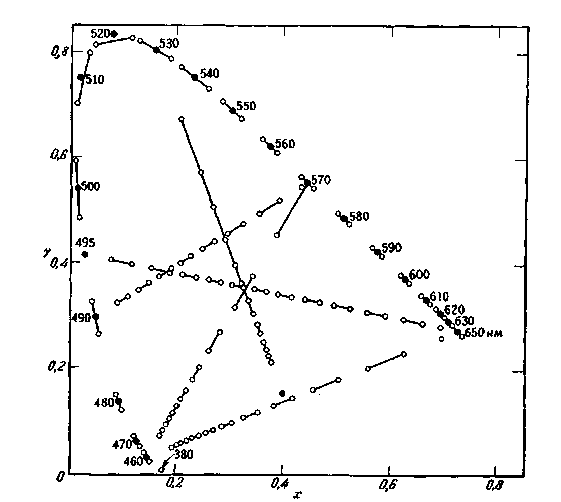
Первую совокупность данных, связанных с восприятием раз­личий цветности вдоль линий спектральных цветностеи и, боль­шого числа линий, образованных аддитивными смесями монохро­матических цветовых стимулов, получил Райт [705, 706]. На рис. 2.78 представлен цветовой график (х, у) МКО 1931 г. с неко-

340 ГЛАВА 2

торыми типичными результатами измерений Райта. Интервал цвет­ности, определенный каждым штрихом на пунктирных линиях, по Райту соответствует цветовому различию, воспринимаемому оди­наковым для всех штрихов. Из рис. 2.78 совершенно очевидно, что

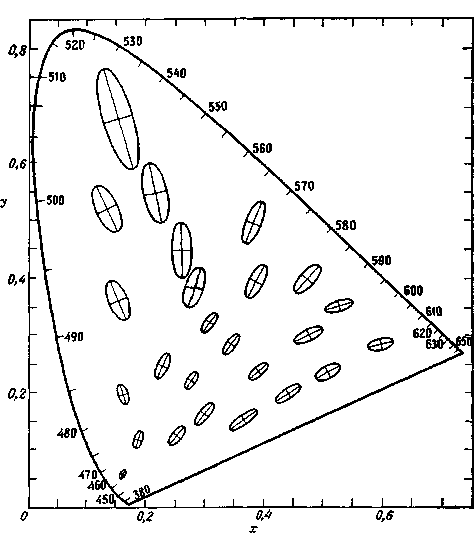
Рис. 2.79. Статистические отклонения уравниваний по цветности в различных

частях цветового графика х, у МКО 1931 г. [398]. Линии эллипсов соответствуют цветностям, отстоящим от центральной точки на вели­чину стандартного отклонения при установке равенства по цветности. Для наглядности оси каждого эллипса увеличены в 10 раз

цветовой график (х, у) МКО 1931 г. далек от равнокошрастного; область зеленых цветов (верхняя часть графика) слишком растяну­та, а синевато-пурпурных (нижняя часть графика) – очень сжата.

Вторая совокупность данных, касающихся в основном подпо-роговых различий цветности, была опубликована Мак Адамом

СРЕДСТВА И МЕТОДЫ КОЛОРИМЕТРИИ 341

[398]. Представляющая интерес величина различий в цветности определялась степенью ошибок, сделанных наблюдателем при установке равенства по цветности. Наблюдаемое поле в 2° имело яркость 48 кд-м^-2 (или ~15 миллиламберт). Расположенное вокруг него поле в 21° имело яркость около 24 кд -м^-2. Поле окру­жения воспроизводит дневной свет (стандартное излучение С МКО). Результаты Мак Адама представлены на рис. 2.79. Каждая иссле­дуемая точка цветности окружена эллипсом, представляющим собой геометрическое место точек, соответствующих различиям в цветности относительно центра и равных стандартному отклоне­нию при уравнивании цветности. Для наглядности оси эллипсов на рис. 2.79 увеличены в 10 раз. Вновь мы отмечаем, что область зеленых цветов на цветовом графике (х, у) выглядит сильно растянутой, а синевато-пурпурных – сжатой.

С помощью дополнительных экспериментов Мак Адам опреде­лил, что едва заметное различие в цветности должно быть почти втрое выше рассчитанного стандартного отклонения при уравни­вании цветов [398]. Это означает, что геометрическими местами точек, соответствующих едва заметным различиям в цветности относительно данной точки цветности, являются эллипсы с осями, примерно втрое длиннее осей эллипсов стандартных отклонений.

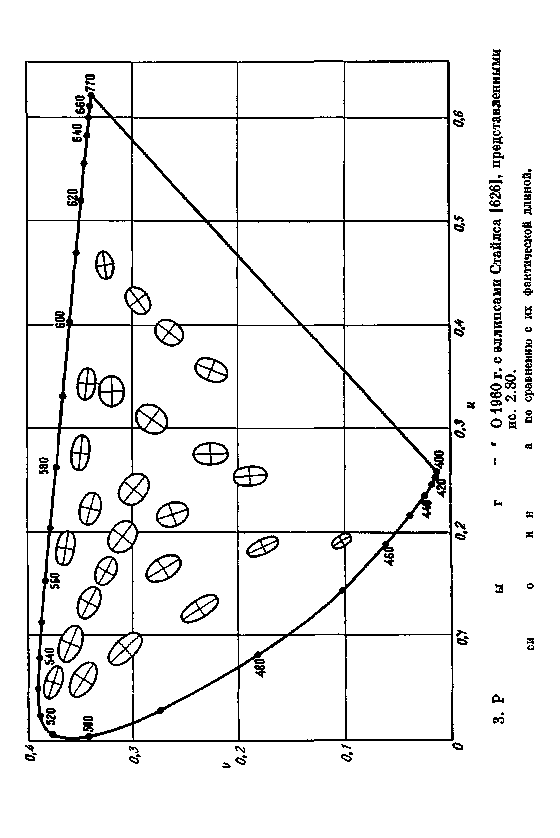
Используя данные экспериментов, касающихся заметных изме­нений цвета, вызванных добавлением излучения одной цветности к излучению другой, Стайлс построил тело расположения цвет-ностей [626]. Поэтому сравниваемые поля отличались как по цвет­ности, так и по яркости [625]. Чтобы учесть увеличение в яркости, вызванное добавлением одного светового потока другим, Стайлс использовал трехкомпонентную теорию зрения Гельмгольца. В этом изящном методе уменьшения, по-видимому, учтена хромати­ческая адаптация и в результатах (рис. 2.80) не содержится локаль­ных неравномерностей, обнаруженных Мак Адамом (рис. 2.79) у своего единственного наблюдателя. Следует отметить, что данные Стайлса подтверждают основные тенденции результатов Мак Адама.

Статистическое непостоянство уравнивания цветов также ши­роко исследовалось Брауном и Мак Адамом [69], Брауном [70– 73], а совсем недавно Вышецким и Филдером [733]. Результаты этих исследователей в целом согласуются с эллипсами, получен­ными Мак Адамом [398] и Стайлсом [626]. Однако абсолютного согласия нет и в ряде случаев отмечены систематические расхож­дения. В связи с этим следует обратить особое внимание на выводы, сделанные Вышецким и Филдером в [733]. Эти авторы подчерки­вают, что данные по визуальному уравниванию цветов, получен­ные одним и тем же наблюдателем в различных случаях, но при одинаковых условиях наблюдения, по-видимому, гораздо менее воспроизводимы, чем это устанавливается обычным статистическим

342 ГЛАВА 2

анализом. Вероятно, на функционирование зрительного механиз­ма, который контролирует уравнивание цветов, влияют параметры, зависящие от времени, а возможно, йот других обстоятельств, не

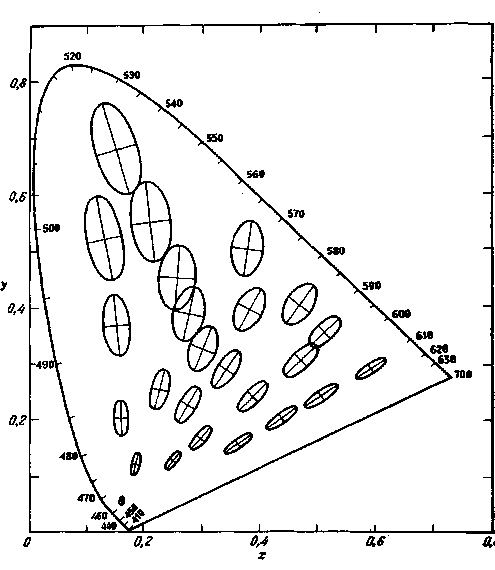
Рис. 2.80. Статистические отклонения уравниваний по цветности, предсказан­ные Стайлсом, в соответствии с преобразованным линейным элементом Гель-мгольца в различных частях цветового графика х, у, МКО 1931 г. [626].

Размер эллипсов увеличен в три раза.

контролируемых обычными статистическими методами. Этим мож­но объяснить иногда довольно значительные отклонения по форме, размерам и ориентации некоторых эллипсов относительно других. Однако, если даже сделать допуск на несовместимость эллипсов отдельных наблюдателей, следует отметить некоторые системати­ческие расхождения между рядами эллипсов различных наблюда-

СРЕДСТВА И МЕТОДЫ КОЛОРИМЕТРИИ 343

телей. В частности, были обнаружены систематические расхож­дения между некоторыми из эллипсов, приведенных Мак Адамом [398], и соответствующими эллипсами, приведенными Брауном и Мак Адамом [69], Брауном [73], Вышецким и Филдером [733]. В основном несоответствия наблюдаются в красной и пурпурной областях цветового графика. Причина их не совсем ясна.

Конечно, следует учитывать также возможность влияния на ориентацию, размер и форму эллипсов различных условий наблю­дения, используемых различными исследователями, однако с не­которой достоверностью по несоответствию между различными совокупностями эллипсов можно выявить лишь влияние величины поля зрения на абсолютный размер эллипсов. С уменьшением раз­мера поля зрения эллипсы увеличиваются. В связи с этим вспом­ним приведенный ранее рис. 2.19.

Следует также ожидать изменения эллипсов при изменении яркости наблюдаемых цветовых стимулов в различных пределах. Более того, предполагается, что яркость, так же как и цветность окружения, оказывает некоторое влияние на непостоянство урав­нивания цветов. Однако условия наблюдений, на которых бази­руются различные совокупности имеющихся данных, касающихся уравнивания цветов, не настолько отличаются друг от друга, чтобы было возможно количественно оценить их предполагаемое влияние на ориентацию, форму и размер эллипсов. Необходимы дальнейшие эксперименты по изучению влияния условий наблю­дения.

Данные по воспринимаемости различий в цветности и связан­ными с ними эллипсами могут быть использованы для проверки равноконтрастности цветового графика МКО 1960 г. Для зтого необходимо перенести пунктирные линии на рис. 2.78 и эллипсы на рис. 2.79 и 2.80 на равноконтрастный график МКО 1960 г. при помощи уравнения (2.59). Результаты такого переноса приведены на рис. 2.81–2.83. Следует отметить, что в отношении однородно­сти интервала цветности график МКО 1931 г. несколько уступает равноконтрастному цветовому графику. Однако равноконтрастный цветовой график МКО 1960 г. не согласуется полностью с экспе­риментальными данными. Ни одна из трех совокупностей данных по экспериментально определенному распределению цветности точно не согласуется с распределением цветности на равнокон-трастном цветовом графике. Штрихи Райта не всегда имеют одну и ту же длину, а эллипсы Мак Адама и Стайлса не являются идеальными окружностями и не равны по величине. Аналогичные результаты имеют место и для эллипсов уравнивания цветов, полу­ченных упомянутыми выше Брауном и Мак Адамом [69], Брауном [73], Вышецким и Филдером [733].

Мак Адам провел тщательный анализ своих данных и доказал, что ни линейным или даже нелинейным преобразованием цвето-

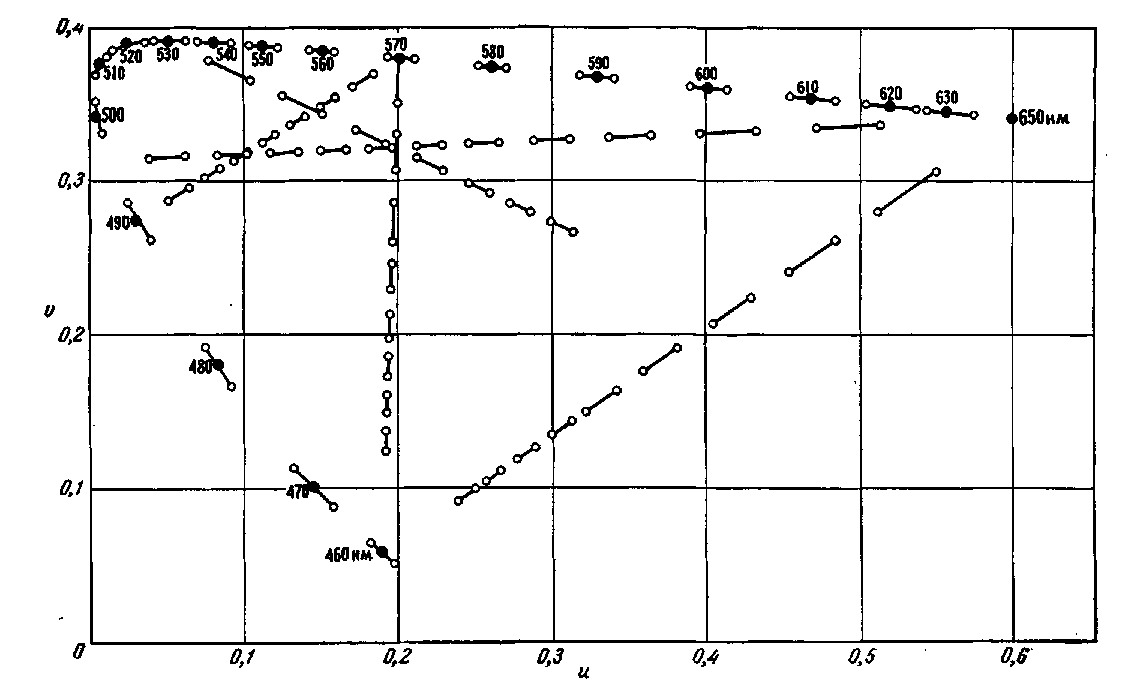
Рис. 2.81. Равноконтрастный цветовой график МКО 1960 г. с отрезками прямых в соответствии с

рис. 2.78 [705].

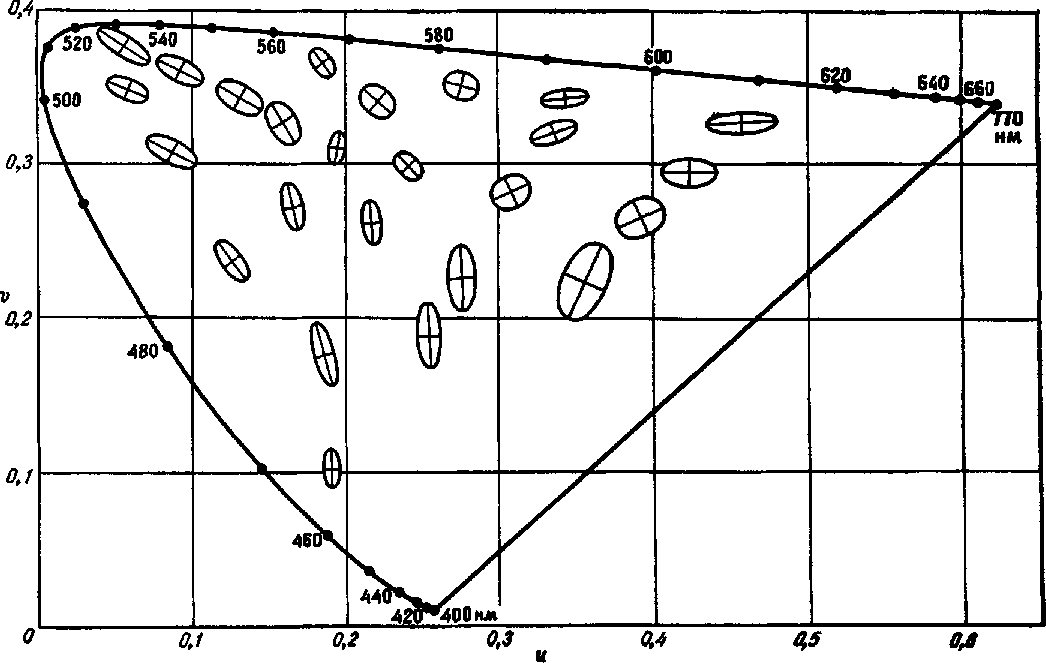
Рис. 2.82. Равноконтрастный цветовой график МКО 1960 г. с эллипсами Мак-Адама [398], представ­ленными на рис. 2.79.

Оси эллипсов Мак Адама увеличены в 10 раз по сравнению с их фактической длиной

СРЕДСТВА И МЕТОДЫ КОЛОРИМЕТРИИ

347

вого графика (х, у) нельзя добиться преобразования эллипсов в идеальные окружности равного диаметра [399, 400]. Чтобы полу­чить идеальные окружности, необходимо использовать не плос­кость, а искривленную поверхность [401, 403]. Эта поверхность напоминает смятую фетровую шляпу с выпуклостью посредине, гофрированную по краям, неровную и кривую на остальных участ­ках. Из рис. 2.82 можно увидеть, с какими трудностями сталки­ваются при попытке представить эллипсы Мак Адама на плоском графике. В центре графика эллипсы имеют тенденцию уменьшаться по размеру и больше напоминают окружности, чем эллипсы на периферии. Для того чтобы на двумерной поверхности различия по цветности, оцененные наблюдателем как одинаково заметные, представить линиями равной длины, поверхность должна быть куполообразной. Для этого средние части графика должны быть меньше, чем показано на рис. 2.82. Если стянуть по окружности центральную часть (х = у = 0,3), то она станет выпуклой, т. е. образует поверхность положительной кривизны.

При дальнейшем рассмотрении рис. 2.82 открывается следую­щая закономерность: главные оси эллипсов на периферии графика в основном имеют тенденцию указывать в направлении к центру. Чтобы на двумерном графике одинаково воспринимаемые разли­чия по цветности представить линиями равной длины, необходимо a»g сжать радиальные отрезки и растянуть периферийные. Это снова

*jj § * заставляет отказаться от плоскости, однако при куполообразной

JQ £ форме поверхности в центральной части радиальные расстояния

^ _и увеличиваются по сравнению с периферийными, что совершенно

_tg я противоположно требуемому типу поверхности, т. е. необходима