2.3 Методика формування вмінь вирішувати тригонометричні нерівності

У процесі формування в школярів умінь вирішувати тригонометричні нерівності, також можна виділити 3 етапи.

1. підготовчий;

2. формування вмінь вирішувати найпростіші тригонометричні нерівності;

3. введення тригонометричних нерівностей інших видів.

Ціль підготовчого етапу полягає в тому, що необхідно сформувати в школярів вміння використовувати тригонометричне коло або графік для рішення нерівностей, а саме:

- вміння вирішувати найпростіші нерівності виду sinx > 1, sinx <-1 , cos x > 1, cosx < -1 за допомогою властивостей функцій синус і косинус;

- вміння становити подвійні нерівності для дуг числової окружності або для дуг графіків функцій;

- вміння виконувати різні перетворення тригонометричних виражень.

Реалізувати цей етап рекомендується в процесі систематизації знань школярів про властивості тригонометричних функцій. Основним засобом можуть служити завдання, пропоновані учнем і виконувані або під керівництвом учителя, або самостійно, а так само навички напрацьовані при рішенні тригонометричних рівнянь.

Приведемо приклади таких завдань:

1. Відзначте на одиничній окружності крапку , якщо

.

2. У якій чверті координатної площини розташована крапка , якщо

дорівнює:

3. Відзначте на тригонометричній окружності крапки , якщо:

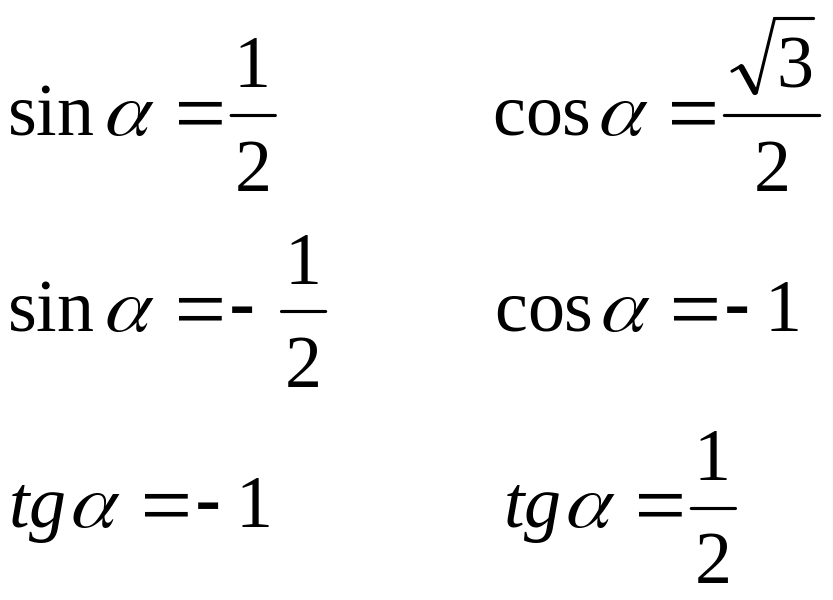
4. Приведіть вираження до тригонометричних функцій I чверті.

а) б) в)

5. Дано дугу МР. М - середина I - ой чверті, Р - середина II-Ой чверті.

Обмежити значення змінної t для: (скласти подвійну нерівність)

а) дуги МР;

б) дуги РМ.

6. Записати подвійна нерівність для виділених ділянок графіка:

7. Вирішите нерівності sinx > 1, sinx <-1 , cos x > 1, cosx <-1

8. Перетворити вираження sin5xcos4 x-cos5xsin4x

Привернимо увагу на завдання 5 і 6. Природно, саме воно лежить в основі рішення найпростішої тригонометричної нерівності.

Нерівності, що характеризують дугу, ми пропонуємо становити в 2 кроки. На першому кроці становимо «ядро» запису нерівності (це, власне кажучи, головне до чого варто навчити школярів); для заданої дуги МР одержимо . На другому кроці становимо загальний запис:

, .

Якщо ж мова йде про дугу РМ, то при записі «ядра» потрібно врахувати, що крапка А(0) лежить усередині дуги, а тому до початку дуги нам доводитися рухатися по першій негативній окружності. Виходить, ядро аналітичного запису дуги РМ має вигляд , а загальний запис має вигляд. ,

При рішенні завдання 7, варто особливо звернути увагу на значимість властивостей тригонометричних функцій.

На другому етапі навчання рішенню тригонометричних нерівностей можна запропонувати наступні рекомендації, пов'язані з методикою організації діяльності учнів. При цьому будемо орієнтуватися на вже наявні в вміння, що вчиться, працювати із тригонометричною окружністю або графіком, сформовані під час рішення найпростіших тригонометричних рівнянь.

По-перше, мотивувати доцільність одержання загального прийому рішення найпростіших тригонометричних нерівностей можна, звернувшись, наприклад, до нерівності виду . Використовуючи знання й вміння, придбані на підготовчому етапі, учні приведуть запропоновану нерівність до виду; , але можуть уcкладнитись в знаходженні множини рішень отриманої нерівності, тому що тільки лише використовуючи властивості функції синус вирішити його неможливо. Цього ускладнення можна уникнути, якщо звернутися до відповідної ілюстрації (рішення рівняння графічно або за допомогою тригонометричного кола).

По-друге, вчитель повинен звернути увагу учнів на різні способи виконання завдання, дати відповідний зразок рішення нерівності й графічним способом і за допомогою тригонометричного кола.

Пропонуємо такі варіанти рішення нерівності

1. Рішення нерівності за допомогою кола.

Вирішимо тригонометричну нерівність .

На першому занятті за рішенням тригонометричних нерівностей запропонуємо учнем докладний алгоритм рішення, що у покроковому поданні відбиває всі основні вміння, необхідні для рішення нерівності.

У зв'язку з реалізацією третього етапу процесу формування в школярів умінь вирішувати тригонометричні нерівності зробимо лише два зауваження.

По-перше, знайомство учнів із прийомами рішення тригонометричних нерівностей, що не є найпростішими, доцільно здійснювати за наступною схемою: звертання до конкретної тригонометричної нерівності звертання до відповідного тригонометричного рівняння спільний пошук (вчитель – учні) прийому рішення самостійний перенос знайденого прийому на інші нерівності цього ж виду.

По-друге, щоб систематизувати знання учнів про тригонометрію, рекомендуємо спеціально підібрати такі нерівності рішення яких вимагає різних перетворень, які можуть бути реалізовані в процесі його рішення, акцентувати увагу учнів на їхніх особливостях.

Як такі продуктивні нерівності можна запропонувати, наприклад, що випливають

Отже, у темі «Тригонометричні нерівності» ми пропонуємо вивчати тільки те, що дасть можливість школярам відчути саме специфіку тригонометричних нерівностей. [11,c.64]