1.3 Види тригонометричних рівнянь і методи їхнього рішення

Матеріал, що ставиться до тригонометрії, вивчається не єдиним блоком, учні не уявляють собі весь спектр застосування тригонометричного матеріалу, дроблення на окремі теми приводить до того, що тригонометрія вивчається протягом декількох років.

Необхідність класифікації рівнянь і нерівностей викликається неможливістю знайти загальний метод їхнього рішення. Очевидно, що класифікувати тригонометричні рівняння й нерівності має сенс із опорою на методи їхнього рішення.

Рівняння, що зводяться до найпростіших

Практично всі тригонометричні рівняння вважаються «найпростішими», але можна виділити ряд рівнянь які зводяться до найпростішого досить просто. Розглянемо спочатку види найпростіших рівнянь.

До найпростіших тригонометричних рівнянь ставляться рівняння виду: , , , .

На ці рівняння варто звернути особливу увагу, тому що без вміння їх вирішувати неможливо вирішити ніяке інше тригонометричне рівняння. Найкраще, якщо учні будуть мати схеми рішення кожного з найпростіших рівнянь [4,c.81]

Р івняння виду .

Якщо , то

Якщо , то (рис 1, а)

Особливі випадки:

;

;

;

Кожна із цих формул може бути замінена формулою загального виду, однак вони простіше і їх вигідніше застосовувати при рішенні рівнянь.

Корисно пам'ятати, що при ; ;

.

Рівняння виду .

Якщо , то

Якщо , то (рис 1, д)

Особливі випадки:

;

;

;

Потрібно пам'ятати, що при ;

;

.

Рівняння, що є рівністю двох однойменних тригонометричних функцій:

а) рівняння виду рівносильно сукупності рівнянь:

б) рівняння виду рівносильно системі рівнянь:

в) рівняння виду рівносильно системі рівнянь:

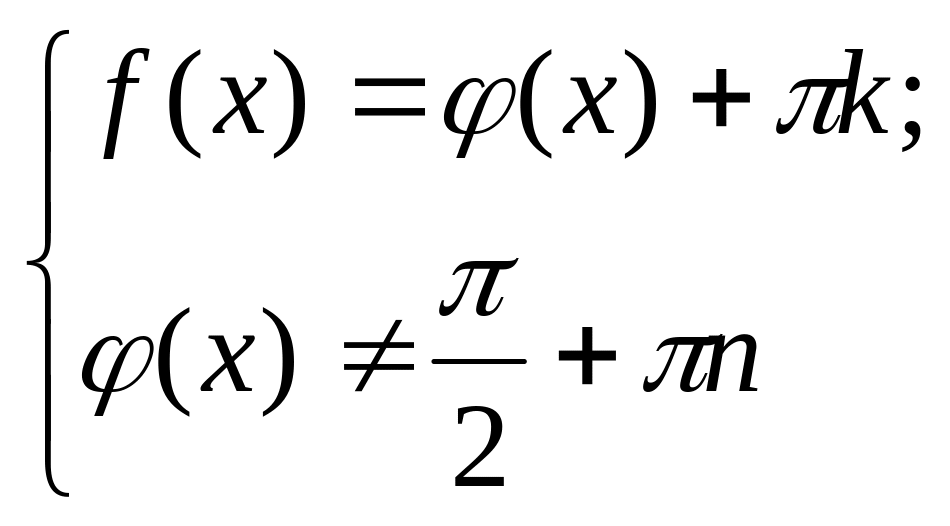
Тригонометричні рівняння, що містять ту саму функцію того самого аргументу й розв'язувані методом підстановки

Рівняння даного виду , де тригонометрична функція часто називаються звідними до квадратного й вирішуються методом підстановки замість тригонометричної функції даного аргументу деякого параметра t з урахуванням припустимих значень t залежно від області значення функції.

Приклад: Вирішите рівняння:

Нехай тоді рівняння прийме вид:

Обидва корені рівняння задовольняють умові припустимого значення t, отже, переходимо до зворотної заміни.

[29]

Однорідні рівняння

Попередньо можна показати учню вид однорідної функції від двох змінних U і V першого ступеня, наприклад, 3U + 2V; другого ступеня: ; третього ступеня: і т.д., сформувавши поняття вираження, однорідного щодо змінних U і V.

Для кращого засвоєння й закріплення ідеї необхідно вирішити з учнями наступне рівняння:

.

Позначимо

Виходить однорідне рівняння другого ступеня:

;

Маємо 2 случаючих: U = V або V = 0,5 U

Як правило, на практиці дуже часто зустрічається .

Приклади:

1. .

Це однорідне рівняння першого ступеня. Обидві частини рівняння потрібно розділити на cosx. При цьому вийде рівносильне рівняння. Щоб у цьому впевнитися, покажемо, що рівняння cosx = 0 не містить корінь даного рівняння.

Дійсно, якщо

, те .

Але це неможливо, тому що .

Отже, маємо рівносильне рівняння

2. .

Це однорідне рівняння другого ступеня. Одержимо рівносильне рівняння після ділення обох частин рівняння на .

[5, c.9]

Рівняння, що вирішуються розкладанням на множники

При рішенні рівнянь такого типу необхідно користуватися відомим правилом: добуток декількох множників дорівнює нулю, якщо хоча б один з них дорівнює нулю, а інші при цьому мають сенс.

Приклади:

1.

Використовуючи дане правило одержимо:

або

2.

Згрупуємо відповідні доданки, одержимо:

Рівняння виду

Один зі способів рішення такого рівняння полягає в тому, що ліву частину рівняння можна перетворити по формулі:

Приклади:

1.

;

, тому що це рішення системи

Підставляючи у формулу, одержуємо:

2.

, тому що це рішення системи

Підставляючи у формулу, одержуємо

На жаль, увага учнів нечасто звертається на перетворення вираження .

У деяких посібниках ця формула наведена в такому виді

де .

Такий запис приведе до помилки, якщо, наприклад, a і b негативні.[10]