1.2 Роль і місце тригонометричних рівнянь і нерівностей у шкільному курсі математики

Тригонометрія традиційно є однією з найважливіших складових частин шкільного курсу математики. І цей курс припускає задачі, вирішити які, як правило, можна, пройшовши цілеспрямовану спеціальну підготовку.

Аналіз шкільних підручників по математиці в повному обсязі визначає місце тригонометричних рівнянь і нерівностей у лінії вивчення рівнянь і лінії вивчення нерівностей.

Вивченню теми «Рішення тригонометричних рівнянь» часто передує вивчення таких тим як «Перетворення тригонометричних виражень» і «Основні властивості й графіки тригонометричних функцій».

Досвід викладання математики показує, що усвідомлення важливості досліджуваного матеріалу приходить до учнів не в процесі його вивчення, а в процесі його застосування при рішенні інших завдань, тобто тоді коли він стає засобом для рішення інших задач.

Так, наприклад, рішення рівняння , зводиться до найпростішого рівняння , причому приватного виду найпростішого, після елементарного перетворення вираження, що стоїть в лівій частині рівняння по формулах додавання косинуса. Аналогічна ситуація може виникнути й при рішенні тригонометричних нерівностей. Нерівності виду 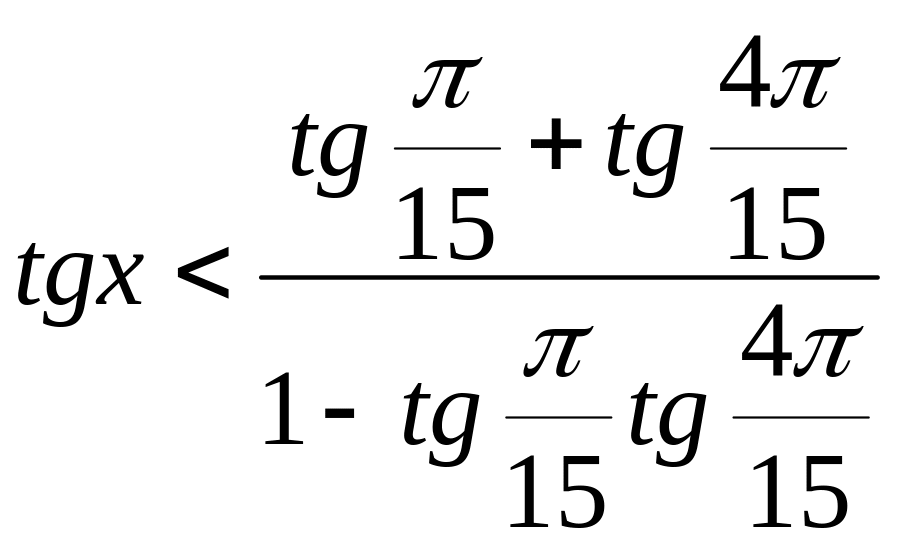, у принципі стають розв'язуваними тільки після перетворення вираження яке стоїть в правій частині нерівності. Одержимо, , а потім за допомогою таблиці значень основних тригонометричних функцій маємо простої нерівність , рішення якого не повинне викликати ускладнень у учнів.

Ми бачимо, що саме тут школярі можуть спостерігати користь від вивчення формул тригонометрії. З їхньою допомогою нерозв'язане на перший погляд рівняння або нерівність приймає досить простий і, головне знайомий вид. Приблизно те ж саме відбувається й при рішенні тригонометричних нерівностей. [9,c.81]

При такому підході вивчення тригонометрії, коли рівняння й нерівності вивчаються після формул перетворення тригонометричних виражень, місце тригонометричних рівнянь і нерівностей визначається через систематизацію знань по темах «Перетворення тригонометричних виражень» і «Основні властивості й графіки тригонометричних функцій».

Якщо ж тригонометричні рівняння й нерівності вивчаються до теми «Перетворення тригонометричних виражень», то тут місце їхнього вивчення визначається зовсім протилежним чином. Тут на вивчення тригонометричних рівнянь приділяється більше часу: як тільки з'являється нова формула, вона відразу ж використовується для рішення рівнянь або нерівностей. Тобто в цьому випадку не формула перетворення є засобом для рішення тригонометричного рівняння або нерівності, а рівняння виступає як засіб закріплення тригонометричних формул.

Таким чином, при будь-якому підході до вивчення тригонометрії, роль вивчення рівнянь і нерівностей незмірно велика, не залежно від місця їхнього вивчення. Ну і як наслідок із цього велике й незмірно місце вивчення методів рішення й тригонометричних рівнянь і тригонометричних нерівностей. Оскільки автори підручників не приділяють належну увагу позначенню методів рішення тригонометричних рівнянь і нерівностей, спробуємо класифікувати рівняння й нерівності, і відповідно методи їхнього рішення. [14,c.67]