1.3. Интерференция корпуса и несущих поверхностей

Рассмотрим физическую картину взаимодействия корпуса и крыльев, полагая, что корпус представляет собой тело враще­ния, а крылья расположены на его цилиндрической части по схеме среднеплана. Пусть геометрические углы атаки крыльев и корпуса равны между собой, т. е. α_κ = α_φ = α (случай «αα»).

Н абегающий на тело невозмущенный поток можно предста­вить как результат наложения друг на друга двух потоков(рис.1.8): параллельного оси тела со скоростью Vcos α и по перечного потока со скоростью V sin α. При малых углах атаки поперечный поток всегда является дозвуковым.

Р

Рис. 1.6. Номограмма для определения, параметра

ассматривая обтекание цилиндрической части тела попе­речным потоком, можно прийти к выводу, что в точках, лежа­щих в плоскости z—z, местные скорости потока больше, чем V * sinα. Согласно теории потенциального обтекания цилиндра несжимаемым потоком местная поперечная скорость на линии z—z определяется выражением , где z — расстояние от оси цилиндра. В частности, в точках А и В у самой поверхности цилиндра (z = D/2) поперечная ско­рость удваивается: V_n = 2Vsin α.

Увеличение поперечной составляющей приводит к тому, что суммарный вектор скорости отклоняется вверх, т.е. возникает отрицательный скос потока:

.

Если на корпусе в плоскости z—z установлены крылья, то их фактический угол атаки будет переменным по размаху: .

В

Рис. 1.7. Номограмма для определения параметра

бортовых сечениях крыльев α* = 2α, а по мере удаления от них вдоль оси z угол α* уменьшается, приближаясь к α. Следо­вательно, нормальная сила консолей в присутствии корпуса должна быть больше нормальной силы аналогичных изолиро­ванных крыльев (Y_1κ > Y_{1 из.κρ}).

Консоли, в свою очередь, оказывают воздействие на обтека­ние корпуса, так как повышенное давление на нижней поверх­ности консолей и разрежение на верхней поверхности передает­ся на соответствующие участки поверхности корпуса. В резуль­тате такого воздействия на корпусе появляется дополнительная сила, которую будем называть индуцированной нормальной си­лой корпуса Y_1iф, поскольку она индуцируется (возбуждается) крыльями.

Суммарная нормальная сила, обусловленная наличием крыльев, равна сумме сил Υ_1κ и Y_1iф.

Введем безразмерные величины — коэффициенты интерфе­ренции:

,

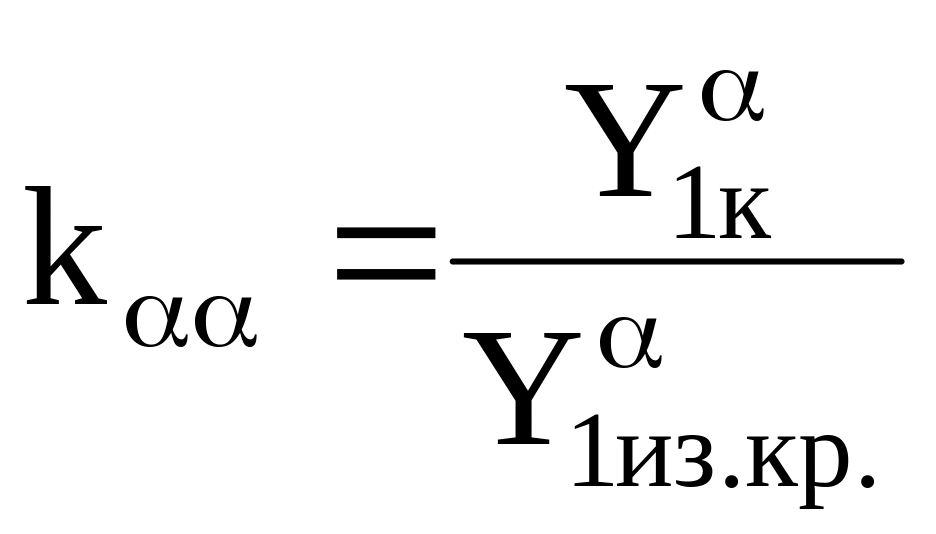К оэффициент k_αα характеризует изменение нормальной силы собственно консолей вследствие влияния на них корпусов, а ко­эффициент K_αα – изменение общей нормальной силы несущей поверхности вследствие взаимного влияния консолей и корпуса. Согласно теории тонкого тела коэффициенты интерференции не зависят от числа Маха и определяются только относитель­ным диаметром корпуса , где

l

Рис. 1.8. К объяснению взаимного влияния корпуса и крыльев

— полный размах несущей поверхности. При D = 0 k_aa = K_αα =1, а с увеличением D коэф­фициенты интерференции возрастают. По теории тонкого тела: (1.12) (1.13) Эта формула представляет собой приближенную аппроксимацию до­вольно громоздкого теоретического выражения.

В ыражения (3.12) и (3.13) совершенно не учитывают таких факторов как сужение консолей, длина хвостовой части корпуса и т. п. Между тем, логические рассуждения и анализ экспери­ментальных данных приводят к выводу, что этими факторами пренебрегать нельзя.

У

Рис. 1.9. Две комбинации кор­пус – крылья, отличающиеся сужением консолей

чет влияния сужения консолей. Сравним две комбинации корпус — крылья с одинаковым значением D, но отличающиеся сужением консолей (рис. 1.9). Как было показано выше, вслед­ствие поперечного обтекания кор­пуса местные углы атаки в сече­ниях консолей будут переменны­ми, достигая наибольшей величи­ны α* = 2α у бортов корпуса и по­степенно уменьшаясь по мере удаления от них.

В варианте 2(η_κ = ∞) -большая часть площа­ди консолей находится в зоне по­вышенных углов атаки, в то вре­мя как в варианте 1 (η_κ=1) пло­щадь консолей распределена в поле углов атаки равномерно. Нетрудно заключить, что относительное увеличение нормальной силы консолей (а следовательно, и индуцированной нормальной силы корпуса) в варианте 2 должно быть больше, чем в вариан­те 1. Другими словами, коэффициенты k_ и К_ должны воз­растать с увеличением сужения консолей.

Опыт подтверждает указанный вывод. Обработка экспери­ментальных данных позволяет рекомендовать следующие зави­симости:

(1.14) 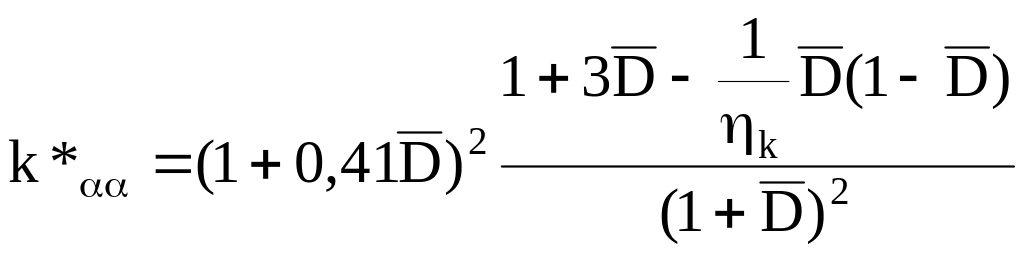(1.15)

Эти зависимости изображены на рис. 3.10 и 3.11. В частном слу­чае, когда η_κ = 1, формулы (1.14) и (1.15) совпадают с теорети­ческими выражениями (1.12) и (1.13).

Учет влияния пограничного слоя корпуса. Влияние корпуса на нормальную силу консолей объясняется не только эффектом поперечного обтекания, но и наличием пограничного слоя. Тол­щина пограничного слоя δ постепенно нарастает по длине кор­пуса, вследствие чего линии тока внешнего потока, обтекающего корпус, оттесняются наружу.

Как известно, величина смещения линий тока δ* носит назва­ние толщины вытеснения.

Для того чтобы приближенно учесть влияние пограничного слоя, заменим действительный корпус с диаметром D условным корпусом с диаметром D'=D+2δ* (рис. 3.12).

При этом, с одной стороны, уменьшится площадь консолей, находящихся во внеш­нем потоке, что приведет к снижению нормальной силы; с дру­гой стороны, из-за увеличения относительного диаметра корпуса возрастет эффект поперечного обтекания, что приведет к повы­шению нормальной силы. Суммарное изменение нор­мальной силы, вызванное влия­нием пограничного слоя, мож­но учесть введением множителя , в котором величины со штрихом соответствуют значению , а величины без штриха – значению . Учитывая, что , и, заменяя на , можно написать ,

. Отсюда, пренебрегая членами, содержащими (δ*)², получим 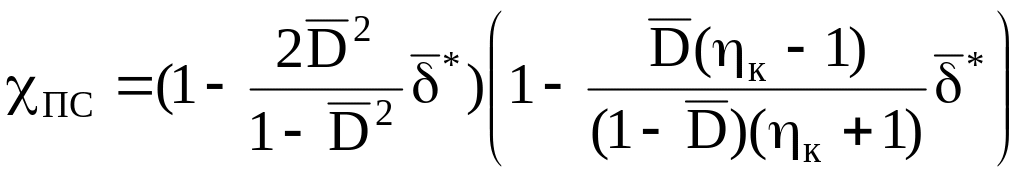(1.16)

Как видно из выражения (1.16), значения χ_ПС всегда меньше единицы.

Относительную толщину вытеснения δ* следует подсчитывать в сечении, проходящем через середину бортовой хорды консо­ли, т. е. на расстоянии от передней точки корпуса. Пользуясь известными теоретиче­скими зависимостями для турбулентного пограничного слоя, можно получить приближенное выражение

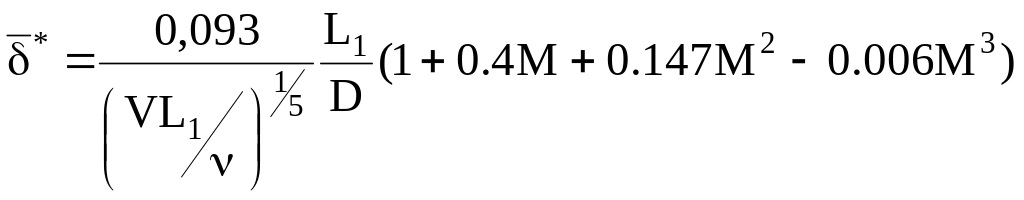(1.17)

в котором ν — кинематический коэффициент вязкости воздуха. Выражение (1.17) справедливо в диапазоне 0<М<15 при от­сутствии теплообмена на поверхности корпуса.

В лияние пограничного слоя оказывается тем сильнее, чем дальше от передней точки корпуса расположена несущая по­верхность и чем больше параметры , η_κ и чис­ло М.

Учет влияния числа Маха. Коэффициенты ин­терференции, подсчитан­ные по теории тонкого те­ла, с поправками на влия­ние сужения консолей и влияние пограничного слоя корпуса, хорошо со­гласуются с эксперимен­том при дозвуковых и небольших сверхзвуковых скоростях (при­мерно до Μ=2). При больших скоростях наблюдается система­тическое расхождение расчета и эксперимента.

Для устранения этого расхождения введем поправочный множитель χ_м, являющийся функцией числа Маха. Значения хм можно определить по эмпирическому графику, изображен­ному на рис. 3,13.

Учет влияния длины передней части корпуса. Выражения (1.12) и (1.13) были получены в предположении о том, что не­сущие поверхности установлены на бесконечно длинном цилинд­ре. Между тем, у некоторых летательных аппаратов (например, имеющих схему «утка») передние поверхности расположены вблизи носика корпуса. В этом случае картина обтекания, по-видимому, отличается от описанной на стр.10, что должно при­вести к изменению коэффициентов интерференции. И действи­тельно, опыт показывает, что по мере уменьшения длины перед­ней части корпуса коэффициенты k_αα. и K_αα уменьшаются.

Для учета этого обстоятельства введем поправочный множи­тель xhoc, приближенно определяемый по эмпирической фор­муле (1.18)

в зависимости от параметра (L1 — расстояние от носи­ка корпуса до середины бортовой хорды консолей). Если в месте расположения консолей диаметр корпуса изменяется, то в расчет следует вводить его значе­ние в середине бортовой хорды консоли.

Учет влияния длины хвосто­вой части корпуса. В теории тон­кого тела предполагается, что избыточные давления (или разре­жения), индуцируемые крылья­ми, распространяются на поверх­ность корпуса в плоскостях, пер­пендикулярных его оси. Зона влияния консолей, в которой со­средоточена сила Y_{1i ф}, представ­ляет собой часть цилиндра, огра­ниченную сечениями АА и ВВ (рис. 3.14). Такое предположе­ние довольно близко к истине в случае дозвуковых и околозвуко­вых скоростей (М≤1).

Однако при сверхзвуковых скоростях волны давления от крыльев сносятся вниз по потоку. В этом случае зона влияния каждой консоли заключена между винтовыми линиями, выхо­дящими из начала и конца бортовой хорды и пересекающими образующие цилиндра под углом Маха (линии АА' и ВВ'). Сме­щение зоны влияния вниз по потоку тем сильнее, чем больше число М. Это смещение отражается прежде всего на положении центра давления летательного аппарата, но при некоторых усло­виях оно влияет на величину нормальной силы.

Если длина хвостовой части корпуса (от конца бортовой хорды до кормового среза корпуса) достаточно велика, то мож­но считать, что индуцируемая крыльями нормальная сила Y_{1i ф} реализуется полностью. Но если длина хвостовой части меньше длины полувитка винтовой линии Маха, т. е. , то часть этой силы теряется, что эквивалентно уменьшению ко­эффициента К_αα.

Выведем приближенную формулу для учета влияния длины хвостовой части корпуса. С этой целью обозначим через q_х по­гонную нагрузку по длине корпуса, вызванную влиянием одной консоли (см. рис. 3.14). Очевидно, что при бесконечно длинной хвостовой части корпуса нормальная сила Y^*_{1i ф}, индуцированная двумя консолями, выразится в виде (1.19)

С другой стороны, при малых углах атаки можно написать со­отношение (1.20)

При короткой хвостовой части корпуса индуцированная нор­мальная сила будет меньше. Обозначим ее Y_1iф: (1.21) Согласно принятым обозначениям,Y_{1i ф}=Y_1из.кр.(K_αα – k_αα) = Y_1из.кр.(K_αα – k_αα) χ_ПС χ_M χ_нос (1.22) Сопоставляя выражения (1.19) — (1.22), найдем K_αα = [k*_αα + (K^*_αα – k^*_αα) F(L_xв)] χ_ПС χ_М χ_нoc, (1.23)

где обозначено 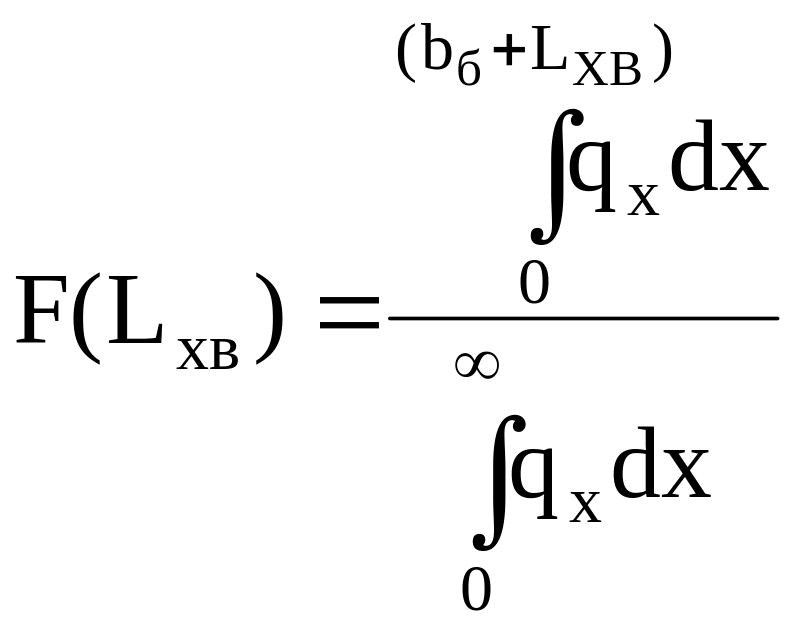(1.24)

Преобразуем последнюю формулу к более удобному виду, для чего введем безразмерные величины 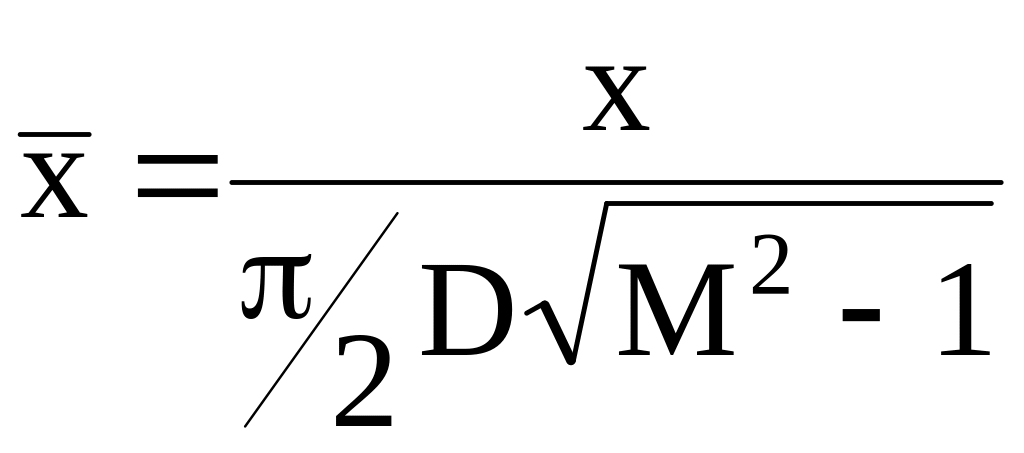, , 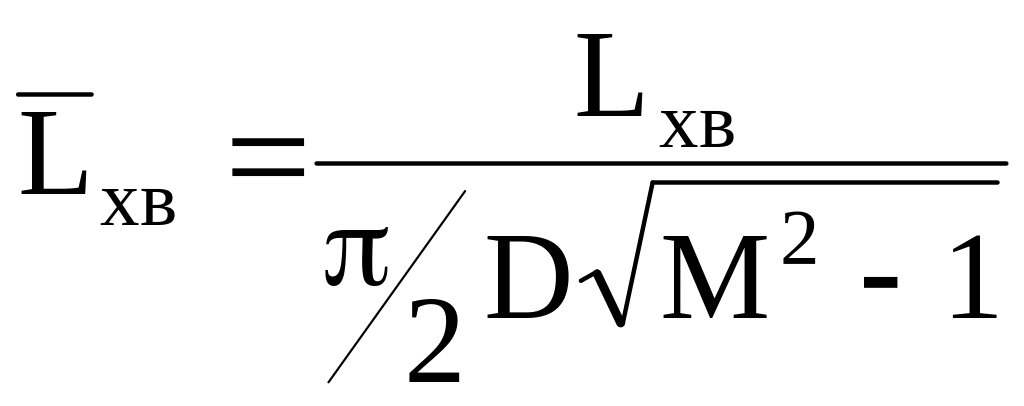(1.25)

В этих выражениях — половина шага винтовой линии Маха.

С учетом соотношений (1.25) формула (1.24) принимает вид 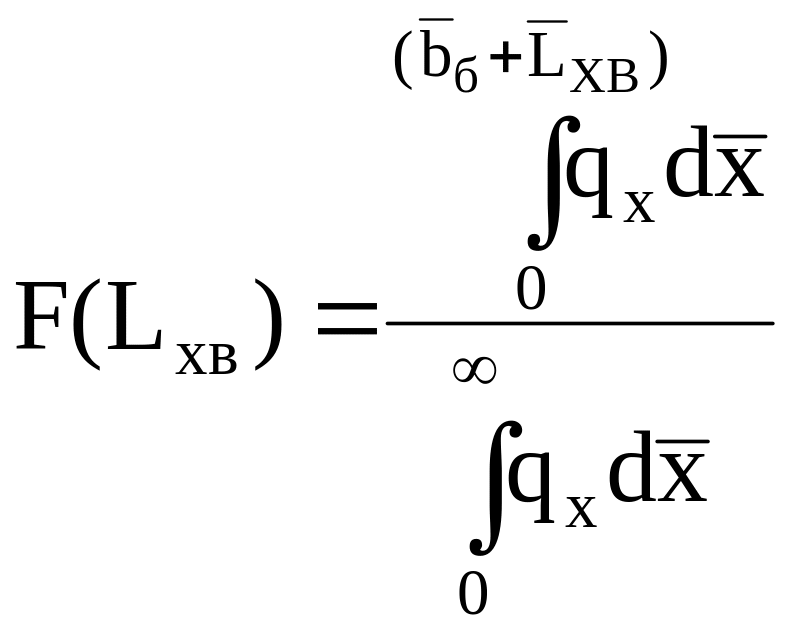(1.26)

Для вычисления входящих сюда интегралов необходимо знать зависимость погонной нагрузки q_x от безразмерной коор­динаты . Имеющиеся экспериментальные данные позволяют рекомендовать следующий вид зависимости:

а) в диапазоне 0 ≤ ≤ (1.27)

а) в диапазоне ≤ ≤ ∞ (1.28)

где А и с — некоторые коэффициенты.

Коэффициент с определяет форму эпюры погонной нагруз­ки q_x. При малых значениях с эпюра получается вытянутой вдоль оси х, а при больших значениях с — сжатой. Эксперимен­тальные данные показывают, что первое соответствует малым значениям , а второе — большим значениям . Некоторое влияние должно, по-видимому, оказывать и сужение консолей: при увеличении η_κ эпюра должна растягиваться, т. е. коэффи­циент с — уменьшаться.

На основании этих соображений можно рекомендовать для расчета с формулу, которая дает приблизительное совпадение с экспериментальными данными: (1.29)

Подставив выражения (1.27) и (1.28) в равенство (1.26) и выполнив интегрирование, получим

(1.30)

Здесь Φ[ζ] — функция Лапласа-Гаусса от аргумента ζ, опреде­ляемая по следующей формуле: , или по следующему графику:

Итак, коэффициент интерференции K_αα определяется выра­жением (3.23). Это выражение, как и формула (1.30) для рас­чета F(L_XB), справедливо во всем сверхзвуковом диапазоне чи­сел Маха (М>1) и при любой длине хвостовой части корпуса. Однако при ручном счете ими целесообразно пользоваться толь­ко в тех случаях, когда параметр не превышает 0,6-0,7, т. е. при достаточно короткой хвостовой части или достаточно больших числах М. Если >0,7, то F(L_BX) ≈ 1 и выражение (1.23) принимает вид K_αα = K^*_αα χ_ПС χ_М χ_нoc (3.31)

Это же выражение справедливо и при М<1.

Коэффициент k_aa во всех случаях подсчитывается по фор­муле k_αα = k^*_αα χ_ПС χ_М χ_нoc (3.32)