МОМЕНТЫ ТАНГАЖА И РЫСКАНИЯ

§ 1. Общее выражение момента тангажа.

СРЕДНЯЯ АЭРОДИНАМИЧЕСКАЯ ХОРДА

При изучении моментов сил, действующих на летательный аппарат, в частности, моментов тангажа, будем пользоваться свя­занной системой координат Ox₁y₁z₁. В этой системе начало коор­динат совпадает с центром масс летательного аппарата; ось Οx₁ направлена вперед, параллельно оси корпуса, ось Оу₁ — вверх, перпендикулярно оси Ох1, а ось Oz1 вправо, перпендику­лярно осям Ох1 и Оy1.

Момент тангажа, или продольный момент, вызывается аэродинамическими и реактивными силами. Рассматривая момент аэродинамических сил, удобно ввести понятие безразмерного ко­эффициента . Здесь S и L — характерные площадь и линейный размер лета­тельного аппарата. В качестве S обычно принимают площадь главной несущей поверхности — крыльев (с подкорпусной частью) или же площадь миделя корпуса. В качестве L целесо­образно брать длину корпуса, однако в ряде случаев за харак­терный линейный размер принимают среднюю аэродинамиче­скую хорду (САХ) крыльев.

Величина аэродинамического момента M_z1 при данной ско­рости и высоте полета зависит от ряда факторов и прежде всего от угла атаки и углов отклонения органов управления. Кроме того, на величину момента влияет угловая скорость вращения летательного аппарата ω_z1, а также скорости изменения угла атаки и отклонения рулей, характеризуемые производными и .

Таким образом M_z1 = f (, _I, _II, _z1, , ) (5.1)

В общем случае эта зависимость имеет сложный, нелинейный характер. Но при малых значениях аргументов нелинейность выражена слабо и поэтому выражение (5.1) можно представить в виде линейной функции:

M_z1 = M_z10 + M^_z1 + M^I_z1_I + M^II_z1_II + M^z1_z1_z1 + + (5.2)

где M^_z1, M^I_z1 и т. д. — частные производные момента тангажа по соответствующим параметрам.

Строго говоря, величина момента Μ_z1 зависит и от некоторых других параметров: угла скольжения, угла отклонения элеронов, угловой скорости вращения летательного аппарата вокруг оси Οχι и т. д. Обычно влияние этих факторов незначительно, поэтому при расчете аэродинамических характеристик им пренебрегают.

Безразмерный коэффициент момента M_z1 является функцией только безразмерных параметров. Так как величины ω_z1, α и δ имеют размерность 1/с, то вместо них вводят безразмерную уг­ловую скорость (5.3)

и безразмерные производные , (5.4)

Общее выражение коэффициента продольного момента при малых значениях параметров α, δI, δII и т.д. имеет вид

m_z1 = m_z10 +  + _I + _II + + +

Входящие сюда частные производные , , , a также m_z10 (коэффициент аэродинамического момента при (α = δ = ω_z1 = α = δ = 0) зависят главным образом от числа Маха и геометрических форм летательного аппарата. Производные ко­эффициента момента по какому-либо углу принято называть статическими производными, а производные по скорости измене­ния того или иного угла – вращательными производными. Таким образом, в выражении (5.5) , , – статические производные, а – вращательные производные.

Для упрощения записи величин, входящих в выражения (5.2) и (5.5), индекс «1» будем в дальнейшем опускать. Кроме того, будем опускать черточки в обозначениях частных производных , , . Таким образом, будет частной производ­ной коэффициента момента m_z1 по безразмерной угловой скоро­сти ω_z1, а M^z_z—частной производной момента Μ_z1 по размерной угловой скорости ω_z1 и т. д.

С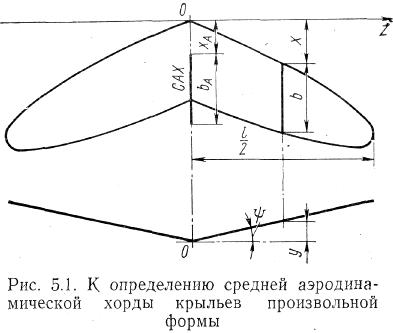 редняя аэродинамическая хорда. Как известно, под средней аэродинамической хордой (САХ) крыльев произвольной формы в плане принимают хорду равновеликих прямоугольных крыль­ев, моментные характеристики которых приблизительно совпа­дают с моментными характеристиками данных крыльев. Величи­на САХ и ее координаты относительно начала корневой хорды (рис. 5.1) определяются следующими выражениями: (5.6)

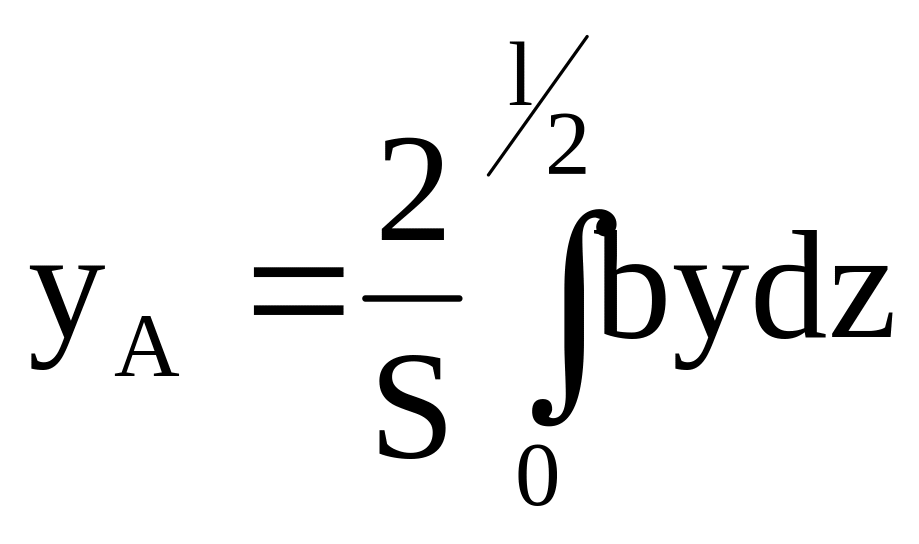(5.7) (5.8)

Эти выражения получены в предположении, что характеристики сече­ний крыла (C_{y1 сеч}, С_х1cеч, C_m0) не изменяются вдоль его размаха.

Середина средней аэродинамической хорды всегда совпадает с центром тяжести площади крыльев.

Для трапециевидных крыльев интегралы можно найти аналитическим путем, так как для них справедливы такие соотношения: (5.9) (5.10)

x=z∙tgχ₀;(5.11) y=z∙tgψ,(5.12) где ψ – угол поперечной V-образности крыльев; .

Подставив выражения (5.9) — (5.12) в (5.6) — (5.8), после интегрирования получим:

(5.13) (5.14) (5.15)

Существует простой графический способ определения САХ трапециевид­ного крыла. Для этого необходимо проделать следующие построения (рис. 5.2):

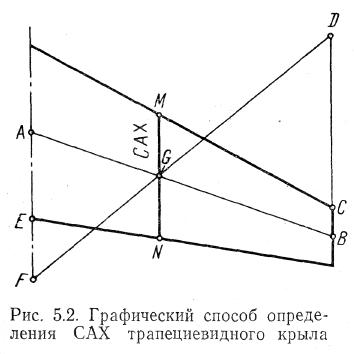
1. провести линию АВ, делящую хорды крыла пополам;

2. на продолжении концевой хорды отложить отрезок CD = b₀, а на про­должении корневой хорды – отрезок EF=b₁. Концы этих отрезков соединить между собой; точка G пересечения линий АВ и DF будет центром тяжести площади трапеции (крыла);

3. через точку G провести хорду MN, которая и будет средней аэроди­намической хордой.

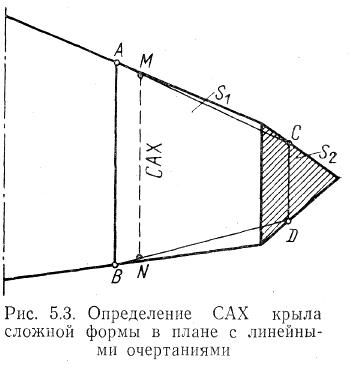
Если крыло имеет более сложную форму в плане (рис. 5.3), то поступают следующим образом:

1. разбивают крыло на две части с площадями S₁ и S₂, каждая из кото­рых представляет собой трапецию или треугольник;

2. находят САХ каждой части описанным выше способом и концы САХ соединяют прямыми АС и BD;

3. отрезок АС делят обратно пропорционально площадям S₁ и S₂, т.е. со­гласно условию ;

4. через найденную таким образом точку Μ проводят прямую ΜΝ, закан­чивающуюся на линии BD.

Отрезок ΜΝ и есть средняя аэродинамическая хорда крыла. Как видно из рис. 5.3, начало и конец САХ не совпадают с передней и задней кромками крыла.

Если крылья имеют криволинейные очертания, то для определения САХ приходится вычислять выражения (5.6) — (5.8) методом графического инте­грирования.

§ 2. МОМЕНТ ТАНГАЖА ПРИ ω_z=α=δ = 0

Рассмотрим величину аэродинамического продольного момен­та, действующего на летательный аппарат, при условии, что угловая скорость ω_z равна нулю, а угол атаки и углы отклонения органов управления остаются неизменными по времени.

В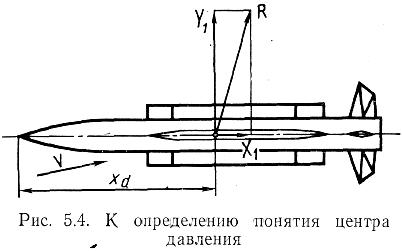 ведем понятие центра давления лета­тельного аппарата. Центр давления – это точка на продольной оси Οx₁, через которую проходит равнодейству­ющая аэродинамиче­ских сил (рис. 5.4). Беспилотные летатель­ные аппараты, как пра­вило, симметричны или почти симметричны от­носительно плоскости x₁Oz₁, поэтому тангенциальная сила Х₁ проходит по оси Ох₁. При этом условии центр давления можно определить как точку приложения равнодействующей нормальных сил Υ₁.

Обозначим координату центра давления, отсчитанную от не­которой точки на оси Ох₁ (например, от носика корпуса), через x_d, а координату центра тяжести аппарата (центровку) через x_T. Тогда момент аэродинамических сил относительно центра тяже­сти можно выразить в виде M_z =Υ₁(x_T –x_d)(5.16), а коэффициент момента (5.17)

По аналогии с понятием центра давления всего летательного аппарата введем также понятия центров давления его частей, как точек приложения нормальных сил, создаваемых этими час­тями. Так как момент равнодействующей, равен сумме моментов ее составляющих, то C_y1x_d = + + . (5.18)

Отсюда находим связь между координатами центров давления частей аппарата x_dф,x_dI,x_dII и координатой общего центра дав­ления:

x_d= [ + + ]. (5.19)

Исключив из равенств (5.17) и (5.19) величину х_d, можно вы­разить коэффициент момента тангажа непосредственно через x_dф, x_dI, x_dII:

m_z = + + (5.20)

При малых углах атаки и углах отклонения рулей удобно пользоваться понятием аэродинамических фокусов летательного аппарата. Как было показано в гл. III, в этом случае нормальная сила может быть представлена в виде линейной функции:

Υ₁ = + + + (5.21)

Каждая из составляющих нормальной силы приложена в опре­деленной точке. Фокусом летательного аппарата по углу атаки называется точка приложения той части нормальной силы, кото­рая пропорциональна углу атаки . (Строго говоря, здесь надо было бы рассматривать не составляющие нормальной силы, а составляющие полной аэродинамической силы.)

Аналогичный смысл имеют понятия фокусов по углам отклонения передних или зад­них несущих поверхностей: это точки приложения тех составляю­щих нормальной силы, которые пропорциональны углам δ_I или δ_II ( и ).

Как видно из приведенных определений, ни один из фокусов, в общем случае не совпадает с центром давления летательного аппарата, т.е. с точкой приложения всей нормальной силы. В частном случае, когда аппарат симметричен относительно плоскости x₁Oz₁ и δ_I = δ_II = 0, центр давления совпадает с фоку­сом по α, так как в этом случае Υ₁ = . Если аппарат симмет­ричен и α = δ_II = 0, то центр давления совпадает с фокусом по δ_I и т.д.

Можно дать и другое определение понятия фокуса. Предста­вим, что поперечная ось Οz₁ проходит через фокус по α, и вычислим момент аэродинамических сил относительно этой оси при закрепленных в определенном положении органах управления (δ_I = δ_II = const). Легко убедиться в том, что этот момент будет постоянным, не зависящим от угла атаки. Действительно, первая составляющая нормальной силы в выражении (5.21) приложена в фокусе по α и поэтому не создает момента, а вторая, третья и четвертая составляющие при δ_I = δ_II = const дают момент посто­янной величины.

Следовательно, фокусом по углу атаки можно назвать точку, обладающую тем свойством, что при закрепленных органах уп­равления момент аэродинамических сил относительно оси Oz₁, проходящей через эту точку, не зависит от угла атаки.

Путем таких же рассуждений легко показать, что момент относительно фокуса по δ_I не зависит от δ_I, а момент относитель­но фокуса по δ_II не зависит от δ_II.

Пользуясь понятиями аэродинамических фокусов, можно на­писать следующее выражение коэффициента момента тангажа летательного аппарата при малых углах α, δ_I и δ_II:

(5.22)

или

(5.23)

(5.24)

(5.25)

(5.26)

В этих выражениях x_Fα, x_FδI и x_FδII – координаты фокусов по α, δ_I и δ_II.