5.7 Распределительные задачи

При рассмотрении транспортной задачи указывалось, что к схеме транспортной задачи относится значительно более широкий круг задач, чем собственно транспортные задачи.

Рассмотрим задачи, модель которых сходна с моделью тран­спортной задачи. Примерами таких задач являются так называе­мые распределительные задачи: об оптимальном распределении производства изделий между предприятиями, о наиболее рациональном закреплении производства изделий между предприятиями, о наиболее рациональном закреплении механизмов за определенными видами работ, об оптимальном распределении посевных площадей между сельскохозяйственными культурами, об оптимальном использовании автотранспорта за счет сокращения порожнего пробега, об оптимальных назначениях и т.д.

Предположим, на предприятии имеется т станков различной мощности , на которых может изготавливать­ся любое из изделий п видов . Известны затраты в рублях на единицу k-го изделия при производстве его на -м стан­ке, а также известна производительность шт./ч -го станка при производстве -го изделия, и наконец, известно плановое за­дание по выпуску изделий . Требуется распределить производство изделий на различных станках так, чтобы минимизировать суммарные затраты при выполнении планового задания.

Условие можно представить в виде таблицы, где – время, в течение которого -ый станок занят изготовлением -го изделия.

Станки	Затраты на единицу изделия, руб., и производительность, шт./ч			Объем имеющихся мощностей, станко-ч.
		…
		…
…	…	…	…	…
		…
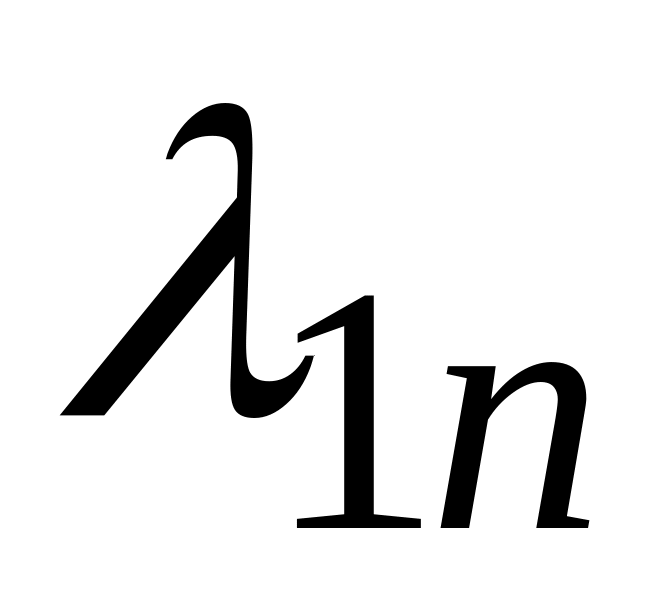
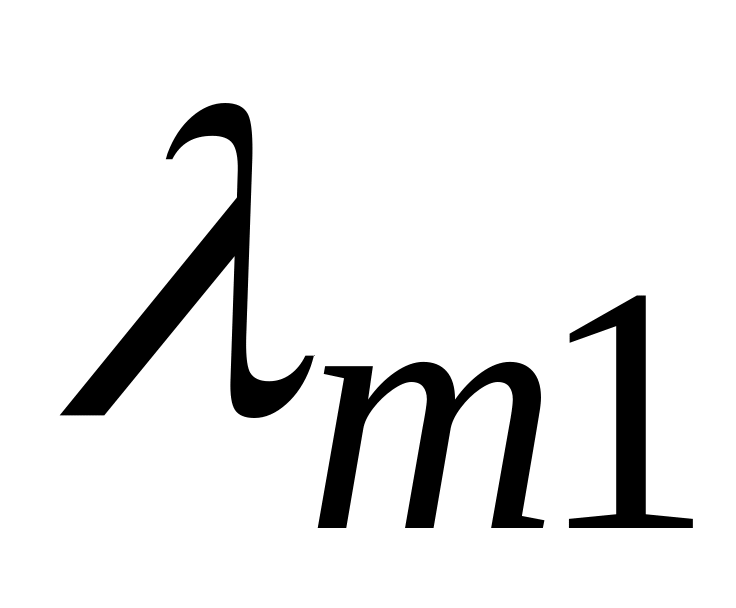
Плановое задание, шт.		…

Математически задачу можно сформулировать так: дана система ограничений

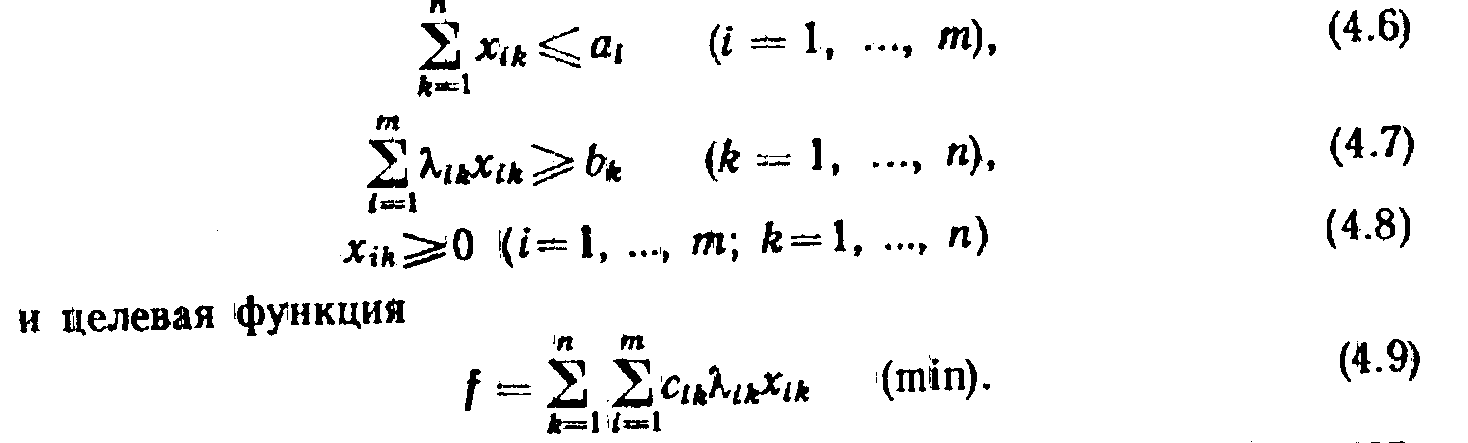
Требуется найти такие значения переменных , которые удовлетворяли бы ограничениям (4.6), (4.7) и условиям (4.8), а целе­вую функцию (4.9) обращали бы в минимум.

Левая часть неравенства (4.6) указывает, что суммарная мощ­ность (станко-ч), затраченная i-м станком, не превышает имеюще­гося объема мощностей на данном станке. Левая часть неравен­ства (4.7) показывает, что всего должно быть изготовлено k-x изделий не меньше планового задания . Как видно из соотноше­ния (4.7), величина определяет количество -х изделий, изготовляемых на i-м станке. Следует заметить, что ограничения (4.6) и (4.7) могут быть совместными (объем имеющихся мощно­стей достаточен для выполнения планового задания) и несовмест­ными (объем мощностей недостаточен).

Таким образом, полученная математическая модель аналогич­на транспортной и отличается от нее наличием множителей . Поэтому ее называют -моделью.

Рассмотрим частный случай решения распределительной за­дачи, когда она приводится к обычной транспортной задаче. До­пустим, что производительность любых двух станков пропорцио­нальна. Выбрав один из станков (пусть для определенности первый) в качестве базового, составляем отношение производительностей любого i-го станка к базовому. Следующие отношения будут равны для всех изделий:

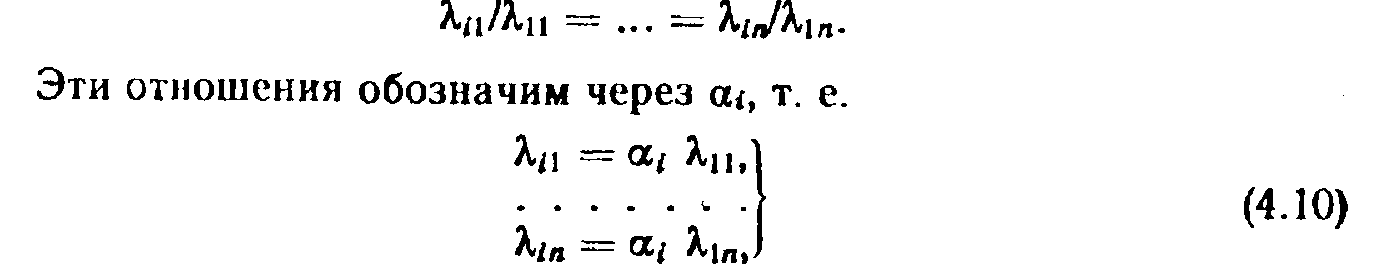
где , есть индекс -го станка (по отношению к базовому). Ра­венства (4.10) позволяют выразить не только производительности всех остальных станков по отношению к производительностям ба­зового станка, но и другие параметры задачи. В этом случае один час работы базового станка принимается за стандартный час.

Тогда мощность -го станка, приведенная к стандартным часам, будет стандартных часов, т. е.

а время, затрачиваемое по плану ('-м станком на производство k-го изделия, выразится в стандартных часах:

-с,иа,=у,А. (4.11)

Плановое задание по А-му изделию составляет &д. Если бы это изделие изготавливалось на базовом станке, то для его произ­водства необходимо было бы стандартных часов

Ь„1К^Ь\ (k^\,...,n). Затраты в расчете на 1 стандартный час составят

С(*^1» -= Oik-

Величины а,, б», сц, называются приведенными к стандартным часам, т. е. мощностями, плановыми заданиями, затратами соответст­венно.

Приводя системы ограничений (4.6), (4.7) и целевую функцию (4.9) к стандартным часам, получаем

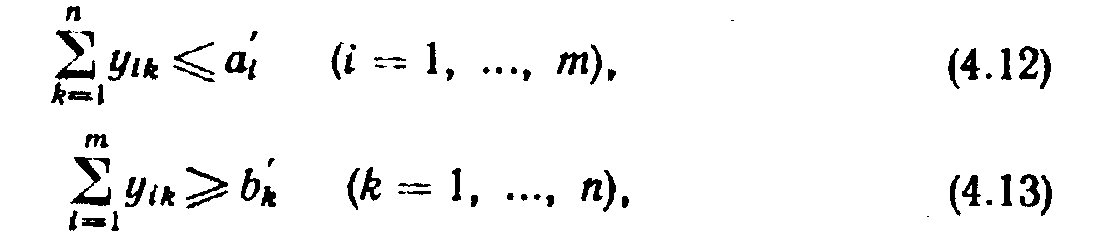
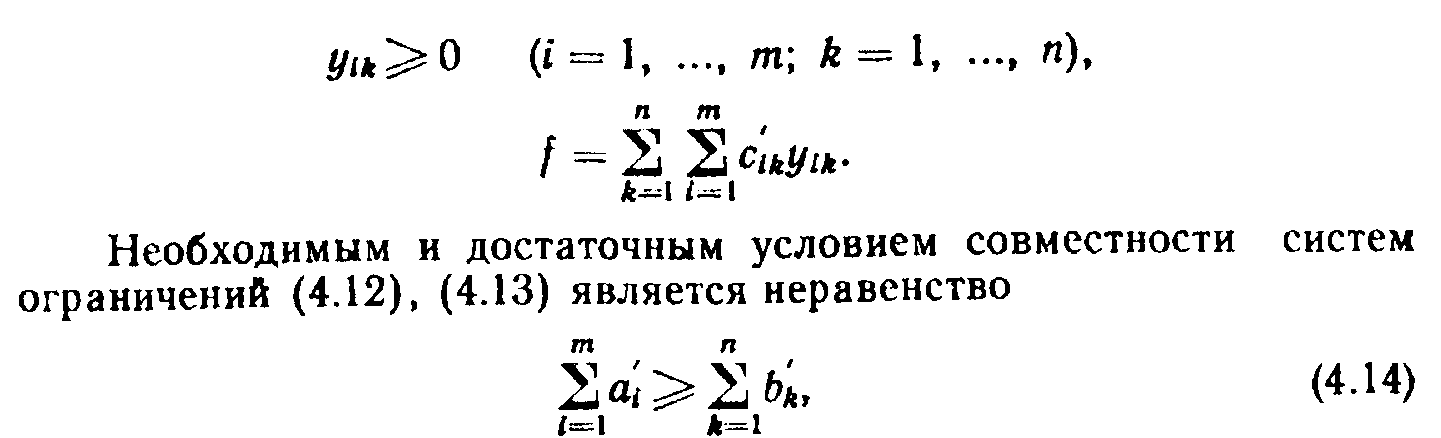
т. с. суммарные приведенные ресурсы должны быть не меньше суммарных приведенных потребностей в стандартных часах. В про­тивном случае план b'=° (&i; ...; Ьп) невыполним.

Если условие (4.14) выполняется как равенство, то и неравен­ства (4.12) и (4.13) превращаются в равенства, и мы приходим к закрытой модели транспортной задачи. После того, как будет най­дено оптимальное решение, необходимо с помощью формул (4.11) вернуться к исходным переменным Xik.