9 Лабораторна робота 4 оцінювання параметрів розподілу по виборці

Мета роботи: ознайомитися з принципами і загальними підходами при оцінюванні параметрів розподілу, вивчити основні методи визначення параметрів розподілу по виборці, дослідити вплив розмірів вибірки на точність оцінювання параметрів, вивчити методику виявлення грубих помилок.

Короткі теоретичні відомості

Основи теорії вибірок.

Параметрами розподілу ймовірностей називають набір чисел, значення яких повністю визначають цей розподіл як конкретний елемент деякої множини імовірнісних розподілів.

Будь-які характеристики розподілу ймовірностей можуть бути виражені через його параметри. Тому одна з головних задач – за спостереженнями над незалежними реалізаціями випадкової величини (тобто по виборці) зробити висновки про параметри її розподілу, наприклад, вказати їх наближені значення або оцінити їх, вказати оцінки.

В залежності від мети методи оцінювання параметрів розподілу можливо поділити на дві групи:

• методи оцінювання параметрів по кінцевій виборці;

• методи оцінювання по виборці, яка необмежено зростає.

В якості характеристик розподілу часто використовують моменти (метод моментів), рідше – квантілі (метод квантілей).

Властивості оцінок. Довірче оцінювання.

Для одних і тих самих параметрів можливі й використовуються різні оцінки, які доцільно порівнювати між собою та вибирати ті, які кращі або володіють потрібними властивостями.

Зазвичай оцінки, що часто використовуються, мають властивості наведені нижче.

Нехай _n – оцінка характеристики розподілу , яка отримана по виборці обсягом n. Тоді:

• оцінка _n називається значною, якщо _n   по ймовірності, коли n  ;

• оцінка _n називається незміщеною, якщо М_n = .

Для вирішення питання про вибір найкращої оцінки, необхідно вміти порівнювати оцінки між собою. Єдиного способу порівняння не існує.

Найчастіше в якості критерію вибирають малість величини М(_n-_n)², а найкращою оцінкою вважають ту, для якої ця величина мінімальна.

Більш загальний підхід полягає в тому, що замість величини (_n-_n)² вибирають іншу невід'ємну функцію "штрафу" W(_n,) за відхилення _n від  (іноді говорять функцію втрат), й найкращою оцінкою вважають ту, для якої математичне очікування величини штрафу є мінімальним.

Оцінки, для яких мінімальна функція втрат, називають оптимальними або ефективними. Хоча слід пам’ятати, що оптимальні властивості оцінок отримано при певних припущеннях, які на практиці можуть і не виконуватися.

В багатьох випадках представляє інтерес не отримання точечної оцінки невідомого параметру , а визначення області в якій цей параметр знаходиться з імовірністю, не меншою ніж задана, наприклад 95 або 99%. Така область називається довірчою областю або довірчим інтервалом.

Метод найбільшої правдоподібності.

Різні методи оцінювання одних і тих самих параметрів розподілу можуть давати різні результати. При певних обмеженнях оптимальним є метод найбільшої правдоподібності.

Згідно з цим методом замість змінних в функцію щільності ймовірностей підставляють елементи вибірки, тобто реалізації випадкових величин. Тоді функція щільності ймовірностей перетворюється в величину, яка називається правдоподібністю і являється функцією невідомого параметру . Метод рекомендує обирати в якості оцінки невідомого дійсного значення параметрі  таке значення, при якому правдоподібність досягає максимуму.

Визначення об’єму вибірки.

Визначення об’єму вибірки є найбільш відповідальною задачею при плануванні спостережень або випробувань, оскільки від цього залежить достовірність результатів.

При визначенні кількості спостережень вважаються відомими наступні початкові дані:

• відносна похибка оцінки відповідного параметру ;

• одностороння довірча ймовірність оцінки параметру ;

• передбачуваний коефіцієнт варіації ;

• закон розподілу випадкової величини, яка спостерігається.

Відносну похибку  вибирають з ряду: 0,05; 0,10; 0,15; 0,20.

Односторонню довірчу ймовірність вибирають з ряду: 0,80; 0,90; 0,95; 0,99.

Мінімальний обсяг спостережень N для оцінки середніх значень визначається:

 для експоненціального закону з щільністю з виразу:

, (4.1)

де - квантіль розподілу хі-квадрат з 2N ступенями волі, яка відповідає ймовірності 1-.

Об’єм виборки у випадку експоненціального закону може бути визначений за табл. 4. 1 (для  = 1).

Таблиця 4.1 – Об’єм виборки при законі Вейбулла розподілу випадкової величини

		Обсяг виборки при коефіцієнті варіації 
		0,4	0,5	0,6	0,8	1	1,2	1,5	1,8	2,0	3,0
0,05	0,80	50	65	100	200	315	500	650	800	1000	-
	0,90	100	200	250	500	650	1000	-	-	-	-
	0,95	150	250	400	650	1000	-	-	-	-	-
	0,99	315	500	800	1000	-	-	-	-	-	-
0,10	0,80	13	25	32	50	100	150	200	250	315	400
	0,90	32	50	65	125	200	315	400	500	500	1000
	0,95	50	80	100	200	400	650	800	800	800	1000
	0,99	100	150	200	400	650	800	1000	-	-	-
0,15	0,80	6	10	15	25	40	80	80	125	125	200
	0,90	15	25	32	65	80	150	200	250	315	500
	0,95	25	40	50	100	150	200	315	400	500	800
	0,99	40	65	100	200	315	500	800	1000	-	-
0,20	0,80	5	8	10	20	25	40	50	65	80	125
	0,90	10	15	20	40	50	80	125	150	200	315
	0,95	15	25	32	50	100	150	200	250	250	400
	0,99	25	40	65	125	150	250	315	400	500	1000

 для закону Вейбулла з щільністю з виразу:

, (4.2)

Об’єм виборки у випадку закону Вейбулла може бути визначений за табл. 4. 1.

 для нормального розподілу з щільністю 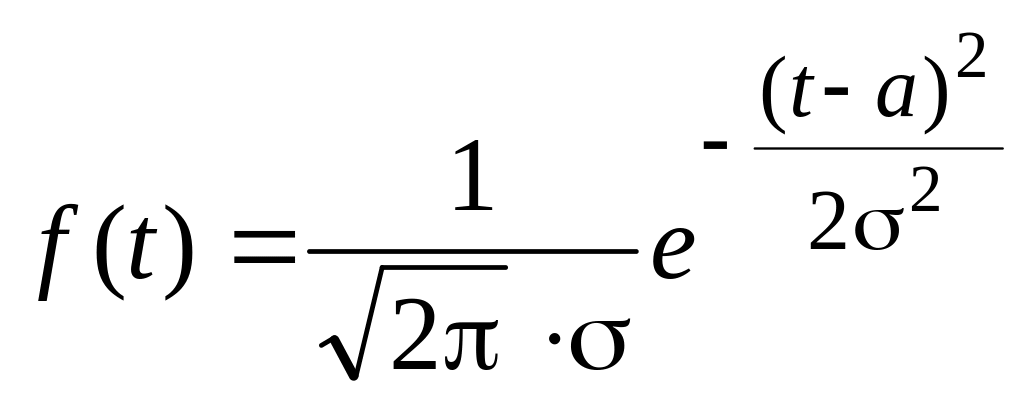з виразу:

, (4.3)

де - кавнтіль розподілу Ст’юдента з N-1 ступенями волі, яка відповідає імовірності .

Об’єм виборки у випадку нормального закону може бути визначений за табл. 4. 2.

 для логарифмічно нормального розподілу з щільністю 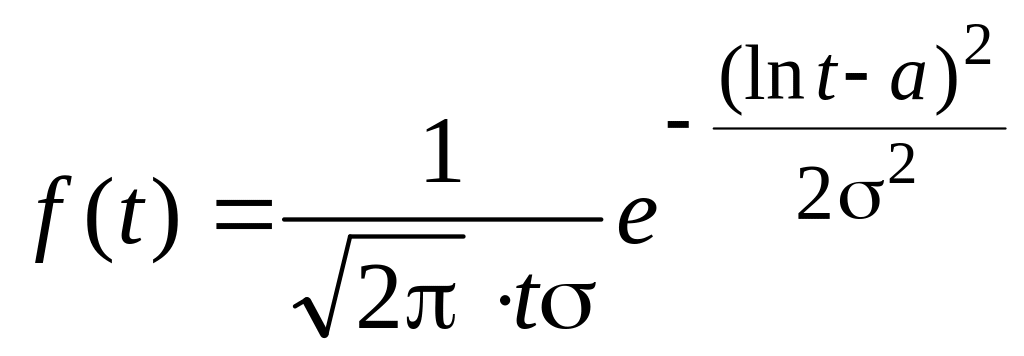з виразу:

, (4.3)

де ; ; - кавнтіль нормального розподілу Ст’юдента, яка відповідає імовірності .

Об’єм виборки у випадку нормального закону може бути визначений за табл. 4. 3.

Таблиця 4.2 – Об’єм виборки при нормальному законі розподілу випадкової величини

		Об’єм виборки при 
		0,10	0,15	0,20	0,25	0,30
0,05	0,80	4	6	13	20	25
	0,90	8	15	25	40	65
	0,95	13	25	40	65	100
	0,99	25	50	100	150	200
0,10	0,80	-	3	5	8	10
	0,90	3	5	8	13	15
	0,95	5	8	13	20	25
	0,99	8	15	25	32	50
0,15	0,80	-	-	3	4	5
	0,90	-	3	4	6	8
	0,95	3	5	6	10	13
	0,99	5	8	13	15	25
0,20	0,80	-	-	-	-	3
	0,90	-	-	4	5	6
	0,95	-	4	5	6	8
	0,99	4	6	8	10	15

Таблиця 4.3 – Об’єм виборки при нормальному законі розподілу випадкової величини

		Об’єм виборки при 
		0,4	0,5	0,6	0,7	0,8	0,9	1,0
0,05	0,80	40	65	100	125	150	200	250
	0,90	100	150	250	315	400	500	650
	0,95	150	250	400	500	650	800	1000
	0,99	315	500	800	-	-	-	-
0,10	0,80	10	20	25	32	40	50	65
	0,90	25	40	65	80	100	125	150
	0,95	40	65	100	125	150	200	250
	0,99	80	125	200	250	315	400	500
0,15	0,80	5	8	10	15	20	25	32
	0,90	13	20	25	40	50	50	65
	0,95	20	32	40	50	80	100	100
	0,99	40	50	80	125	150	200	200
0,20	0,80	3	4	6	8	10	15	20
	0,90	6	10	15	20	25	32	40
	0,95	10	15	25	32	40	50	65
	0,99	20	32	50	65	80	100	125

Обсяг спостережень визначається в наступному порядку:

1. Задаються наступні початкові дані - відносна похибка оцінки відповідного параметру ; одностороння довірча ймовірність оцінки параметру ; передбачуваний коефіцієнт варіації ; закон розподілу випадкової величини, яка спостерігається.

2. Визначається попередній обсяг спостережень N_п.

3. За результатами N_п визначаються параметри розподілу й, зокрема, вибірковий коефіцієнт варіації _в.

4. Якщо _в >  необхідним є додатковий обсяг спостережень. Додатковий обсяг спостережень визначається так само, як і попередній, але підставляється знайдене значення вибіркового коефіцієнту варіації _в.

При визначенні обсягу спостережень N_п або N за допомогою електроних таблиць Excel необхідно скористатися наступними функціями:

• для експоненціального закону та закону Вейбулла (величина 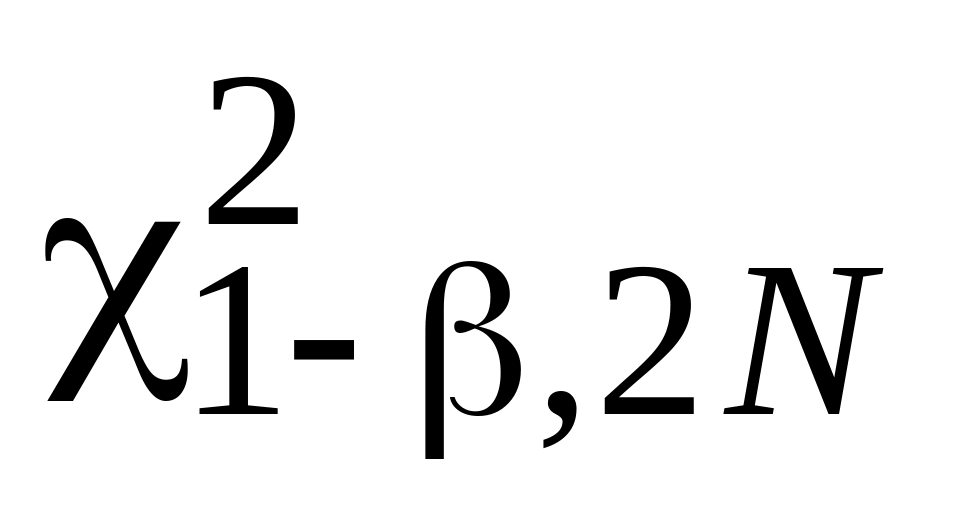) – ХИ2ОБР;

• для нормального закону (величина 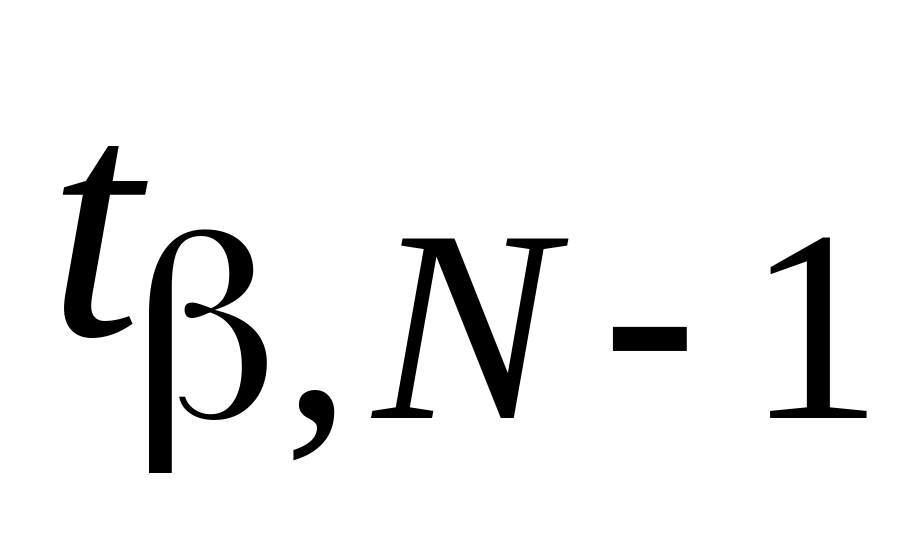) – СТЬЮДРАСПОБР.