VI. Оптика

§ 30. Свет как электромагнитные волны. Интерференция

Оптика — это учение о физических явлениях, связанных с распро­странением коротких электромагнитных волн, длина которых со­ставляет приблизительно Ю^-5 -г- Ю^-7 м. Значение именно этой об­ласти спектра электромагнитных волн связано с тем, что внутри нее в узком интервале длин волн от 0,40 до 0,76 мкм лежит участок ви­димого света, непосредственно воспринимаемого человеческим гла­зом. Этот участок составляет лишь малую часть всей шкалы элект­ромагнитных волн.

Видимый свет и оптический диапазон. С точки зрения физики происходящих процессов выделение столь узкой области видимого света не имеет особого смысла, поэтому в понятие «оптический ди­апазон» включают обычно еще и инфракрасное и ультрафиолето­вое излучение. Но и для них принятые границы спектра достаточно условны. По существу, эти границы определяются используемыми способами получения и регистрации электромагнитных волн.

Излучение электромагнитных волн происходит при ускоренном движении электрических зарядов. Электромагнитные волны радиоди­апазона излучаются антеннами радиопередатчиков при вынужден­ных колебаниях электронов в антеннах. Все электроны в антенне совершают колебания в одинаковой фазе. Поскольку эти колебания могут поддерживаться очень долго и с высоким постоянством частоты, то излучаемые при этом радиоволны с огромной степенью точности можно считать монохроматическими.

Когерентные и некогерентные волны. В оптике все иначе. Лю­бой источник света — это скопление множества возбужденных или непрерывно возбуждаемых атомов. Генератор световой вол­ны — это каждый отдельный атом вещества. Возбужденный атом излучает цуг волн, т. е. отрезок почти монохроматических волн конечной протяженности. Характерной особенностью каждого эле­ментарного источника является его самостоятельность, независи­мость от других атомов. Поэтому даже в том случае, когда отдельные цуги можно характеризовать одной и той же длиной волны л, соотношения фаз между цугами волн, излученных раз­ными атомами, имеют совершенно случайный характер и меня­ются от цуга к цугу.

Только в лазере, где используется вынужденное излучение, уда­ется заставить все возбужденные атомы излучать электромагнитные волны согласованно, подобно тому, как это происходит в антенне радиопередатчика. В результате образуется световая волна, близкая по своим свойствам к идеальной монохроматической, — когерент­ная электромагнитная волна.

Излучение обычных источников света, таких, как раскаленные твердые и жидкие тела, возбужденные электрическим разрядом га­зы и т. д., представляет собой наложение огромного числа не согла­сованных между собой цугов волн, т. е. фактически «световой шум» — беспорядочные, как говорят, некогерентные колебания электромагнитного поля.

Интерференция света. Прямым подтверждением волновой природы света может служить интерференция — явление наложения не­скольких волн, при котором в одних местах происходит усиление, а в других ослабление амплитуды результирующей волны.

Наблюдать интерференцию света от некогерентных источников можно, только используя специальные приемы — разделяя исход­ный пучок на два. Хотя в каждом из этих пучков, как и в исход­ном, фазовые соотношения между различными цугами непрерывно хаотически меняются, эти изменения будут одинаковыми для обо­их пучков. Если эти пучки снова свести вместе, то можно наблю­дать устойчивую интерференционную картину при условии, что разность хода между пучками не превышает длины отдельного цу­га. Если же разность хода окажется больше длины цуга, то устой­чивой интерференционной кар­тины не будет, так как в этом случае будет происходить нало­жение цугов, излученных разны­ми атомами.

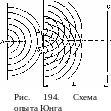
Явление интерференции света впервые было объяснено на осно­ве волновых представлений Т. Юнгом в 1802 г. Для интерпре­тации опыта Юнга можно вос­пользоваться принципом Гюйген­са, который справедлив не только для механических волн, но и для волновых процессов любой при­роды. В опыте Юнга малое отвер­стие А в непрозрачном экране (рис. 194) освещалось интенсивным источником света. На основании принципа Гюйгенса это отверстие можно считать новым точечным источником полусферических волн. Эти волны падают на два малых отверстия 5, и S₂ в следующем эк­ране, которые в свою очередь становятся новыми точечными источ­никами волн.

Таким способом в опыте Юнга достигается разделение исходной волны на две. Эти волны налагаются друг на друга в области за от­верстиями и могут интерферировать, так как источники S_x и S₂ ко­герентны. На экране В образуется интерференционная картина.

Разделение волн от первичного некогерентного источника на две когерентные волны, т. е. получение двух вторичных когерентных точечных источников, может осуществляться разными способами. Но расчет интерференционной картины во всех таких случаях про­изводится одинаково, так же, как и в схеме Юнга. Если в излучении первичного источника все независимые цуги волн характеризуются одной и той же длиной волны X, то для изучения вторичных источ­ников Sj и S₂ можно использовать монохроматическую идеализа­цию, несмотря на то, что их излучение представляет собой ту же хаотическую последовательность отдельных цугов.

Замена такой последовательности цугов бесконечной синусои­дальной волной возможна при условии, что точечные вторичные ис­точники когерентны, а разность хода излучаемых ими волн в любой точке экрана В меньше протяженности отдельного цуга. Для этого, разумеется, экран В должен быть удален от источников S_x и S₂ на значительное расстояние L, а рассто­яние d между источниками 5_t и S₂ должно быть достаточно мало.

Схема Юнга. Схема расчета интер­ференционной картины ясна из рис. 195. В точке О, расстояния до которой ОТ ИСТОЧНИКОВ 5j И S₂ одина- р_ис. 195. к расчету интерферен-КОВЫ, прИХОДЯЩИе ВОЛНЫ усиливают ционной картины в опыте Юнга

друг друга, так как колебания поля в

этой точке происходят в одинаковой фазе. Результат сложения ко­лебаний в произвольной точке Р определяется разностью хода I волн, приходящих в Р из S_x и S₂. Если I равно целому числу длин волн X, то колебания в точке Р усиливают друг друга; если I равно нечетному числу полуволн, то колебания взаимно ослабляются.

Выразим разность хода I волн, приходящих в точку наблюде­ния Р, через угол 0 между осью и направлением на точку Р и расстояние d между источниками (рис. 195).

Будем считать, что d«L. Тогда при малых 9 разность хода можно найти, опуская из S_x перпендикуляр на прямую S₂P:

l = dQ. (1)

Формула (1) дает возможность определить угловое положение максимумов и минимумов на экране В (рис. 195). Направления на

максимумы получим, полагая в (1) 1 = пк:

(2)

Полагая / = (2п + 1) Х/2, получим направления на минимумы:

(3)

Угловое расстояние Д0 между соседними максимумами или ми­нимумами, как видно из этих формул, равно Х/d, а расстояние h между ними на экране В, как видно из рис. 195, равно

h = L Д0 = \L/d.

(4)

Интерференционные полосы. Мы рассмотрели только точки экра­на В, лежащие в плоскости чертежа на рис. 195. Легко сообразить, что вся интерференционная картина на экране В в непосредствен­ной близости от точки О состоит из чередующихся светлых и тем­ных полос, называемых интерференционными полосами. Они нахо­дятся на равных расстояниях друг от друга и направлены перпенди­кулярно плоскости чертежа, т. е. плоскости, в которой лежат первичный точечный источник S (т.е. отверстие А на рис. 194) и вторичные источники S_x и S₂.

Трудность наблюдения интерференции света в таких опытах свя­зана с тем, что длина волны света очень мала. При к = 5- Ю^-5 см и расстоянии d между источниками, равном всего 0,5 мм, расстояние между соседними интерференционными полосами будет составлять только 1 мм при удалении экрана В на 1 м от источников.

Освещенность экрана, т. е. вызываемое светом зрительное ощу­щение, определяется энергией колебаний в световой волне, т. е. квадратом ее амплитуды. Рассчитаем распределение освещенности на экране, где наблюдается интерференционная картина. Если при освещении экрана несколькими некогерентными источниками скла­дываются освещенности, то при интерференции складываются на­пряженности полей в когерентных волнах, а освещенность в каждой точке экрана пропорциональна квадрату амплитуды результирую­щего колебания. Поскольку расстояния от источников до точки на­блюдения почти одинаковы, то амплитуды обеих волн в точке на­блюдения практически равны, если вторичные источники S, и S₂ одинаковы. При этом напряженность поля в точке наблюдения про­порциональна выражению, которое представляет собой сумму коле­баний, вызываемых каждой из волн в точке Р:

cos со(/ — /,/с) + cos со(/ + 1₂/с) =

= 2 cos [со (1₂ — /_т)/2с]

cos со

[*-(/, + /₂)/2с].

Видно, что это есть уравнение колебаний с амплитудой 2 cos (со//2с), зависящей от разности хода / = 1₂ — 1_Г Так как осве­

идейность пропорциональна квадрату амплитуды, то распределение освещенности E(Q) в зависимости от направления на точку наблю­дения 8 имеет вид

2с

^{£(e)~4cos2^ = 4cos2 f^9] =2}

i+cos(^e

(5)

_aaAaa.

e

О

А d

^Ld

d

Рис. 196. Распределение освещенности в интерференционных полосах, наблюдае­мых по схеме Юнга

Распределение освещенности в интерференционных полосах, на­блюдаемых по схеме Юнга, показано на рис. 196. Освещенность в ми­нимумах равна нулю, а в макси­мумах она в четыре раза больше освещенности, которая создава­лась бы одним источником. Поло­жение максимумов и минимумов, как видно из формулы (5), нахо­дится в соответствии с получен­ными ранее формулами (2) и (3).

Отметим, что среднее значе­ние освещенности по экрану в интерференционной картине, со­гласно формуле (5), равно просто удвоенной освещенности от одно­го источника. Это значит, что при интерференции происходит толь­ко перераспределение энергии в пространстве.

Интенсивность наблюдаемой в опыте Юнга интерференционной картины можно заметно увеличить, если вместо точечных отвер­стий А, 5[ и 5₂ в экранах использовать узкие, длинные, парал­лельные между собой щели. Вид полос вблизи центра интерферен­ционного поля будет при этом таким же, как и при использовании точечных отверстий. Поясним это. Если точечное отверстие А пе­ремещать перпендикулярно плоскости чертежа на рис. 194, то ин­терференционные полосы на экране, получаемые от точечных от­верстий 5[ и 5₂, просто будут смещаться вдоль своих направлений, т. е. также перпендикулярно плоскости чертежа. Поэтому замена отверстия А длинной щелью, т. е. непрерывной цепочкой точечных некогерентных источников, не приведет к ухудшению четкости ин­терференционных полос по крайней мере в той области, где их кривизна незначительна. Не приведет к ухудшению четкости и пе­ремещение по этому направлению отверстий S_x и 5₂. Поэтому их также можно заменить на узкие длинные щели.

Зеркала Френеля. В качестве другого примера интерференционно­го опыта, который может быть рассчитан по схеме Юнга, рассмот­рим метод наблюдения интерференции света с помощью зеркал Френеля. Вторичными когерентными источниками S_x и 5₂ здесь яв­ляются изображения реального источника света S в плоских зерка­лах, расположенных под малым углом а друг к другу (рис. 197). Экран защищен от попадания прямых лучей от источника S.

Выясним прежде всего, в каких точках экрана будет наблюдать­ся интерференционная картина. Будет ли она занимать весь экран или какую-то его часть? Интерференция света наблюдается только там, где происходит наложение волн, пришедших от когерентных источников. В данном опыте нужно определить ту область экрана, в любую точку которой свет приходит после отражения от каждого из

Рис. 197. Изображения реального источника света в плоских зеркалах, расположен­ных под малым углом друг к другу

зеркал. На рис. 197 построены изображения S_{ и S₂ точечного ис­точника S в обоих зеркалах. Нетрудно убедиться, что центр окруж­ности, на которой лежат точки S, S_x и S₂, находится в точке А — вершине угла, образованного зеркалами. Из рисунка видно, что ин­терференционное поле на экране ограничено точками В_у и В₂. На­пример, В₂ является крайней нижней точкой, в которую еще прихо­дит свет после отражения от верхнего зеркала. Ее можно найти, ес­ли провести прямую через изображение источника S_{ в верхнем зеркале и точку А. Аналогично находится точка B_v

Из рис. 197 видно, что для расчета интерференционной картины действительно можно воспользоваться схемой Юнга и всеми получен­ными выше для нее формулами. Так как область интерференции на экране ограничена точками В_{ и В₂, то легко подсчитать число интер­ференционных полос. Если экран расположен так, как показано на рисунке, т. е. параллельно линии S_XS₂, соединяющей изображения ис­точника в зеркалах, то В_ХВ₂ = 2a-tg а, где а — расстояние от линии пересечения зеркал до экрана. Учитывая малость угла а между зер­калами, можно приближенно написать В_УВ₂« 2аа. Расстояние h между двумя соседними полосами дается формулой (4). Расстояние d между источниками S_{ и S₂, как видно из рис. 197, равно 2га. Рас­стояние до экрана L равно г + а. Поэтому, согласно (4),

, Х(г + а) ^{Л = _}2г^--

Полное число полос интерференции N, умещающихся на интер­ференционном поле, равно

N ■

X (а + гУ

Так как интерференционную картину удобно наблюдать при усло­вии г<к а, то N ~ Аа²г/Х. Отметим, что в опыте с зеркалами Фре­неля, в отличие от опыта Юнга, можно наблюдать лишь небольшое число интерференционных полос, так как когерентные волны нала­гаются лишь в ограниченной части экрана.

Интерференционные явления, исторически послужившие экспе­риментальным доказательством волновой природы света, и в наши дни находят важные практические применения, в частности в спек­троскопии и в метрологии. Элементарная теория, основанная на ис­пользовании монохроматической идеализации для световых волн, вполне пригодна для описания действия приборов, применяемых в большинстве интерференционных исследований. При этом можно считать, что поведение отдельных пучков интерферирующих лучей подчиняется законам геометрической оптики, и полностью пренеб­регать дифракционными явлениями.

волны с малой разностью

I I 1/1 ТГ I I

Интерферометр Майкельсона. В рассмотренных выше интерфе­ренционных опытах интерферируют хода — порядка нескольких длин волн. Но существуют и такие интер­ференционные приборы, в которых разность хода может быть сделана весьма большой. Эти приборы назы­ваются интерферометрами.

м₉

1'+2'

интерферометра

Рис. 198. Схема Майкельсона

На рис. 198 приведена упрощенная схема интерферометра Майкельсона. Свет от некоторого источника падает слева на полупрозрачное зеркало А и разделяется на два пучка: отражен­ный 1 и прошедший 2. После отраже­ния от зеркал М, и М₂ эти пучки сно­ва падают на полупрозрачное зеркало

А и частично отражаются, а частично проходят через него. В резуль­тате на экране Р можно наблюдать интерференцию лучей Г и 2'.

Картина интерференции зависит от разности хода лучей, кото­рая определяется разностью «плеч» интерферометра. Одно из зеркал (М₂ на рис. 198) может перемещаться с помощью микрометрическо­го винта, оставаясь параллельным самому себе. При его перемеще­нии изменяется разность хода и интерференционные полосы на эк­ране Р смещаются. Смещение интерференционной картины на одну полосу происходит при перемещении зеркала М₂ на расстояние, равное половине длины волны.

Интерферометр Майкельсона используется для выполнения осо­бенно точных измерений длины. Например, в метрологии с его по­мощью производится сравнение оптического эталона длины, т. е. длины волны оранжевой линии криптона-86, со вторичными этало­нами, выполненными в виде твердых стержней.

• Чем отличаются электромагнитные волны, излучаемые антенной радио­передатчика, и световые волны, излучаемые раскаленным телом?

• Что такое когерентные и некогерентные электромагнитные волны? При­ведите примеры.

• В максимумах интерференционной картины от двух источников осве­щенность может вчетверо превышать освещенность, создаваемую одним источником. Нет ли здесь нарушения закона сохранения энергии?

• Объясните, почему в опыте Юнга четкость интерференционных полос не ухудшается, если заменить точечные отверстия длинными узкими па­раллельными щелями.

• Как зависит ширина интерференционных полос в опыте Юнга от рас­стояния между щелями и от расстояния до экрана?

• Поясните ход лучей в интерферометре Майкельсона и объясните, каким образом в нем можно изменять разность хода интерферирующих волн.

• Объясните, почему в интерферометре Майкельсона интерференционная картина смещается на одну полосу при перемещении одного из зеркал на расстояние, равное половине длины волны.

• Каким образом интерферометр Майкельсона используют для точных из­мерений длины?