§ 27. Незатухающие электромагнитные колебания

До сих пор мы изучали колебательные системы, в которых происхо­дили либо свободные электромагнитные колебания, определяемые начальными условиями, которые в реальных системах всегда зату­хают, либо вынужденные, происходящие под действием приложен­ного внешнего синусоидального напряжения. Однако незатухающие колебания возможны не только при периодическом внешнем воздей­ствии, но и в некоторых других случаях — в так называемых авто­колебательных и параметрических системах.

Автоколебания отличаются от остальных колебательных процес­сов тем, что для их поддержания не требуется периодических воздей­ствий извне. Незатухающие колебания поддерживаются благодаря способности автоколебательных систем управлять поступлением энергии от постоянного источника. Форма, амплитуда и частота ко­лебаний задаются самой системой. Примеры автоколебаний — коле­бания воздуха в органной трубе при поступлении в нее равномерного потока воздуха, колебания силы тока в контуре радиотехнического генератора, колебания маятника или баланса в механических часах.

Параметрические колебания возможны при периодическом из­менении какого-либо параметра колебательной системы — длины маятника, жесткости пружины осциллятора, емкости конденсатора колебательного контура и т. п. Характерным примером такого воз­буждения колебаний, называемого параметрическим резонансом, может служить раскачивание качелей, когда находящийся на них человек регулярно приседает и выпрямляется, периодически пере­мещая тем самым положение центра масс системы.

Автоколебания. Характерные элементы автоколебательной систе­мы, или, как говорят, генератора незатухающих колебаний, — это резонатор, источник энергии и обратная связь между резонатором и источником энергии. Резонатор представляет собой систему, в ко­торой могут происходить собственные затухающие колебания. При­мерами резонаторов могут служить маятник настенных часов или баланс наручных, колебательный контур в ламповом генераторе, струна в смычковом музыкальном инструменте.

Обратная связь представляет собой устройство, с помощью кото­рого генератор сам регулирует поступление энергии от источника. Иначе говоря, благодаря обратной связи осуществляется воздействие результатов процесса на само его течение. В автоколебательных сис­темах обратная связь приводит к усилению интенсивности процесса. Такая обратная связь называется положительной. В системе проис­ходит раскачивание собственных колебаний, т. е. самовозбуждение.

Обратная связь в приведенных примерах осуществляется анкер­ным механизмом в часах катушкой обратной связи в генераторе электромагнитных колебаний, индуктивно связанной с колебатель­ным контуром.

Наличие затухания в резонаторе приводит к диссипации энергии колебаний. Однако обратная связь обеспечивает необходимое вос­полнение энергии, так что амплитуда колебаний нарастает до тех пор, пока потери меньше, чем вносимая в систему энергия. С уве­личением амплитуды колебаний вследствие нелинейных свойств системы это поступление энергии ограничивается и при некоторой амплитуде сравнивается с потерями. Как и при вынужденных коле­баниях под действием периодической внешней силы, при автоколе­баниях, независимо от начального состояния, в конце концов уста­навливается стационарный режим колебаний с определенной часто­той и амплитудой. Но в отличие от установившихся вынужденных колебаний, где частота и амплитуда определяются внешним воздей­ствием, в случае автоколебаний как частота, так и амплитуда опре­деляются только свойствами самой системы.

Механическая модель автоколебательной системы. Автоко­лебания возможны только при наличии положительной обратной связи в нелинейных физических системах. Поэтому анализ урав­нений, описывающих даже самые простые реальные автоколеба­тельные системы, представляет собой сложную задачу. Мы рассмотрим упрощенную модель автоколебательной системы, допу­скающую сравнительно простое исследование — модель обыкно­венных часов с маятником или балансом в качестве осциллятора, способного совершать собственные затухающие колебания. Прин­цип работы часов заключается в том, что при колебаниях маятни­ка в поле тяжести или крутильных колебаниях баланса на спи­ральной пружине осциллятор получает короткий толчок от заве­денной пружины в направлении своего движения, который немного увеличивает его скорость.

Фазовая траектория. Действие часов легко проиллюстрировать с по­мощью фазовой диаграммы, на которой по оси абсцисс отложено сме­щение осциллятора из положения равновесия, а по оси ординат — его скорость (или импульс). При изменении состояния осциллятора изо­бражающая точка на фазовой плоскости описывает некоторую траек­торию. В отсутствие обратной связи фазовая траектория представляла бы собой скручивающуюся спираль, соответствующую затухающим колебаниям (рис. 169а). В стационарном режиме установившихся ко­лебаний фазовая траектория замкнута и при двух «подталкиваниях» за период имеет вид, показанный на рис. 1696. Дважды за период, в моменты прохождения через положение равновесия осциллятор сам «отпирает» канал обратной связи, по которому энергия заведенной пружины передается осциллятору. На фазовой диаграмме этому соот-

ветствуют практически вертикальные изломы траектории, описываю­щие мгновенные увеличения скорости на некоторую величину.

При высокодобротном осцилляторе, собственные колебания кото­рого затухают слабо и, следовательно, потери энергии за период не­велики, размер этих вертикальных участков мал по сравнению с размером фазовой траектории. Это значит, что автоколебания в та­кой системе будут почти гармоническими. Частота этих автоколеба­ний практически совпадает с частотой собственных затухающих ко­лебаний.

Амплитуда установившихся автоколебаний. Амплитуда устано­вившихся колебаний также определяется свойствами самой систе­мы. Значение этой амплитуды можно определить из условия, что в стационарном режиме уменьшение скорости из-за трения за по­ловину периода должно в точности компенсироваться ее увеличе­нием при получаемом от пружины толчке. Обозначим увеличение угловой скорости осциллятора за один толчок через Q. Амплитуда скорости, равная произведению частоты колебаний со на ампли­туду А отклонения от равновесия, при затухающих колебаниях убывает как e^_v'. Поэтому для определения амплитуды А прирав­няем уменьшение амплитуды скорости за половину периода Т/2 увеличению скорости Q при толчке:

Лео - Лео е~ч^тп = Q,

откуда

При слабом затухании, когда уТ«1, формулу (1) для стацио­нарной амплитуды можно упростить, воспользовавшись приближен­ным соотношением е^х « 1 4- х при х« 1. Учитывая, что со = 2л/Т, получаем

А яа Q/jiv. (2)

Видно, что амплитуда А установившихся автоколебаний тем боль­ше, чем сильнее толчки (чем сильнее заведена пружина) и чем меньше затухание у собственных колебаний осциллятора.

Устойчивость автоколебаний. Режим установившихся автоколеба­ний характеризуется устойчивостью. При любых отклонениях амп­литуды как под действием случайных, так и преднамеренных при­чин реакция системы такова, что амплитуда возвращается к своему установившемуся значению. Подтолкнем маятник настенных часов, чтобы размах его колебаний стал больше. Вы увидите, что букваль­но через несколько колебаний амплитуда станет такой же, как и прежде.

Устойчивость режима установившихся автоколебаний легко по­нять из энергетических соображений, учитывая, что должен обеспе­чиваться баланс поступающей от пружины и рассеиваемой энергии за период колебаний. Если амплитуда колебаний вдруг станет боль­ше, то возрастут и потери энергии за период, превысив поступление энергии. И наоборот, уменьшение амплитуды от установившегося значения приводит к превышению поступающей энергии над поте­рями на трение. Амплитуда начнет увеличиваться.

Предельный цикл. Устойчивость установившихся автоколебаний можно понять, рассматривая процесс выхода системы на предельный цикл, которому соответствует замкнутая фазовая траектория на рис. 1696. Если, например, отклонить осциллятор автоколебательной системы на небольшой угол и отпустить без начального толчка, выход фазовой траектории на предельный цикл будет происходить так, как показано на рис. 170а. Фазовая траектория постепенно приближается к предельному циклу изнутри. Напротив, если начальное отклонение

превышает значение установившейся амплитуды, фазовая траекто­рия приближается к предельному циклу извне (рис. 1706).

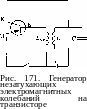Электромагнитные автоколебания. Действие генератора незату­хающих электромагнитных колебаний аналогично рассмотренному механическому примеру автоколебательной системы. Схема такого генератора на транзисторе с колебательным контуром в цепи кол­лектора показана на рис. 171. Роль за­водной пружины, пополняющей энергию колебаний, играет постоянный источник энергии — батарея. Колебательный контур управляет этим источником че­рез цепь обратной связи, содержащую индуктивно связанную с ним катушку Ь_съ, включенную в цепь эмиттера. Транзистор здесь играет роль вентиля, открывающего доступ энергии батареи в колебательный контур. Управление этим вентилем осуществляется подавае­мым с катушки L_CB напряжением к пе­реходу эмиттер—база. Благодаря этому

отпирание транзистора происходит в нужные моменты времени, чтобы импульс тока от батареи пополнял энергию колебаний, ком­пенсируя потери на сопротивлении катушки и проводов.

Параметрический резонанс. Еще один способ возбуждения незату­хающих колебаний, как отмечалось в начале этого параграфа, заклю­чается в периодическом изменении какого-либо параметра колеба­тельной системы. Пусть в колебательном контуре конденсатор устроен так, что можно изменять его емкость, например сближая или раздви­

гая пластины, и пусть в контуре уже существуют колебания неболь­шой амплитуды. В тот момент, когда заряд на пластинах конденсатора максимален, раздвинем мгновенно пластины, немного уменьшив тем самым его емкость. При этом придется совершить некоторую работу, которая пойдет на увеличение электростатической энергии.

В момент, когда ток в контуре максимален, а конденсатор пол­ностью разряжен, сблизим пластины до прежнего расстояния. При этом никакой работы не совершается, и электромагнитная энергия контура остается прежней. Еще через четверть периода колебаний, когда заряд снова достигнет максимального значения (в противопо­ложной полярности), опять раздвинем пластины, добавив тем са­мым еще порцию энергии, и т. д. Таким образом, периодически из­меняя емкость конденсатора в нужные моменты времени, можно до­биться раскачки электромагнитных колебаний, если добавляемая за период энергия превосходит потери в контуре за то же время. Такой способ возбуждения колебательной системы называется параметри­ческим возбуждением контура или параметрическим резонансом.

В отличие от вынужденных колебаний под действием периодиче­ской вынуждающей силы, когда резонанс происходит при совпаде­нии частоты вынуждающей силы с собственной частотой, парамет­рический резонанс возможен при частоте изменения параметра, вдвое превышающей собственную: со = 2со₀. Параметрическая рас­качка колебаний может также происходить, когда параметр изменя­ется не только дважды за период собственных колебаний, но и когда он изменяется один раз за период, два раза за три периода, один раз за два периода, и т. д.

Порог параметрического резонанса. Параметрический резонанс представляет собой пороговый эффект, так как он наступает только тогда, когда поступление энергии превосходит потери, т. е. ампли­туда изменения параметра превышает некоторое пороговое значе­ние. В линейной колебательной системе при превышении порога происходит неограниченное нарастание амплитуды колебаний. Свя­зано это с тем, что при параметрическом резонансе и потери, и по­ступление энергии пропорциональны квадрату амплитуды.

Этим параметрический резонанс в линейной системе отличается от вынужденных колебаний при силовом воздействии, где поступле­ние энергии пропорционально первой степени амплитуды, а поте­ри — по-прежнему квадрату амплитуды, что приводит, как мы ви­дели, к конечной амплитуде установившихся вынужденных колеба­ний. При параметрическом резонансе рост амплитуды ограничен только нелинейными свойствами колебательной системы.

Параметрический резонанс и вынужденные колебания. При не­посредственном силовом воздействии энергия возбужденных колеба­ний возникает за счет работы внешней силы, совершаемой при дви­жении системы. При параметрическом воздействии увеличение за­

паса энергии колебаний происходит обязательно с превращением энергии одного вида в другой. Так, например, механическая работа, производимая при изменении емкости конденсатора в моменты раз-движения его пластин, приводит к изменению запаса электро­статической энергии и, следовательно, общего запаса энергии коле­баний в контуре. Заметим, что параметрическое возбуждение коле­баний возможно лишь при изменении одного из энергоемких параметров, С или L, с которыми связана энергия электрического и магнитного поля. Очевидно, что изменение диссипативного пара­метра R не может вызвать раскачки колебаний.

В заключение отметим еще раз основные различия вынужденных колебаний и параметрического резонанса. Резонанс при вынужден­ных колебаниях возникает при со ~ со₀ (или со = cOq/гс с целым п при возбуждении короткими толчками), но сами колебания сущест­вуют при любой частоте внешнего воздействия. В случае парамет­рического воздействия колебания возникают лишь при выполнении соотношения со«2ш₀/п. Резонанс при вынужденных колебаниях вызывает любая, сколь угодно малая внешняя сила. Для возникно­вения параметрического резонанса амплитуда внешнего воздействия должна превышать некоторое пороговое значение.

• В чем заключается принципиальное отличие автоколебаний и парамет­рических колебаний от вынужденных колебаний осциллятора? Чем они отличаются друг от друга?

• Приведите известные вам примеры автоколебательных систем. Какие элементы должна обязательно содержать автоколебательная система? Каковы их функции? Что такое обратная связь?

• При каких условиях установившися автоколебания будут почти синусо­идальными? От чего зависит их частота и амплитуда?

• Что такое предельный цикл на фазовой диаграмме? Докажите, что при любых начальных условиях в рассмотренной механической модели ав­токолебательной системы фазовая траектория постепенно приближается к предельному циклу изнутри или извне, нигде его не пересекая.

• Объясните подробно, каким образом в генераторе незатухающих элект­ромагнитных колебаний транзистор через катушку обратной связи обес­печивает поступление импульсов тока от батареи как раз в те моменты времени (и в нужном направлении), когда ток в катушке L колебатель­ного контура максимален. Что будет, если переключить (поменять мес­тами) концы одной из этих катушек?

• Постройте примерный график зависимости заряда конденсатора от вре­мени при параметрической раскачке колебаний, вызванной периодиче­скими изменениями емкости.

• Почему для возникновения параметрического резонанса амплитуда из­менения параметра должна превышать некоторое пороговое значение?

• Покажите, что при параметрическом резонансе рост амплитуды колебаний ограничивается нелинейными свойствами системы, например, неизохрон­ностью (зависимостью периода собственных колебаний от амплитуды).

а Релаксационные колебания. Во всех упоминавшихся выше примерах автоколебательных систем обязательным элементом являлся резонатор. Другими словами, в отсутствие обратной свя­зи в этих системах возможны собственные затухающие колеба­ния. При наличии обратной связи в них устанавливаются само­поддерживающиеся почти синусоидальные колебания. Частота таких колебаний задается резонатором.

Но автоколебания могут происходить и в системах, не содержа­щих резонатора. Колебания при этом, как правило, не являются

h

I'i О

Рис. 172. Типичный пример релаксационных колебаний

гармоническими. Типичными примерами таких систем могут слу­жить генератор пилообразных колебаний на неоновой лампе и гид­равлическое устройство, показанное на рис. 172. В сосуд, снабжен­ный сифоном С, с постоянной скоростью натекает вода из крана К. Пока сифон не заполнен водой, уровень воды в сосуде растет со временем по линейному закону. Но как только уровень достигает высоты А,, сифон срабатывает и уровень воды

, Л, А

Рис. 173. Фазовая ди­аграмма релаксаци­онных колебаний, по­казанных на рис. 172

в сосуде падает до значения А₂, после чего со­суд снова начинает заполняться водой из кра­на. Скорость опорожнения сосуда через сифон у_г можно сделать гораздо больше скорости его наполнения через кран v,, так как скорость воды в сифоне зависит от разности уровней А₂ и А₃. Далее описанный процесс будет повто­ряться периодически. Зависимости уровня во­ды А и скорости его изменения и от времени показаны в правой части рис. 172. Видно, что колебания уровня воды и скорости не являют­ся синусоидальными. Соответствующая этим колебаниям фазовая диаграмма приведена на рис. 173.

Аналогичные процессы происходят в генераторе пилообразных колебаний на неоновой лампе. Его электрическая схема показана на рис. 174. Неоновая лампа Л обладает тем свойством, что ток че­

рез нее не проходит до тех пор, пока приложенное к лампе напря жение не достигнет определенного значения, называемого напря жением зажигания U₃. Если после возникновения тлеющего раз ряда в лампе напряжение на ней не­сколько уменьшить, то лампа будет продолжать гореть. Ток через лампу прекратится лишь тогда, когда на­пряжение будет уменьшено до опре­деленного значения, называемого напряжением гашения U_T.

При замыкании ключа конден­сатор С начинает медленно заря­жаться через сопротивление R.

Как только напряжение на конденсаторе достигнет значения, равного напряжению зажигания лампы U₃, в лампе возникает газовый разряд и конденсатор начинает быстро разряжаться че­рез лампу, так как сопротивление горящей неоновой лампы очень мало. Когда напряжение на конденсаторе уменьшится до значения гашения U_T, разряд в лампе прекращается и конден­сатор опять начинает заряжаться. Затем все повторяется снова. График зависимости напряжения на конденсаторе от времени U(t) приведен на рис. 175.

Автоколебания, происходящие в генераторе на неоновой лам­пе и рассмотренном выше гидравлическом устройстве, носят на­звание релаксационных. Для таких колебаний характерно постепенное накопление энергии систе­мой до некоторого значе­ния, а затем быстрое «из­бавление» от накопленной энергии. Аналогом нако­пительного бачка в гид­равлическом устройстве является конденсатор в генераторе пилообразного напряжения; аналогом сифона является неоновая лампа, а роль крана играет сопротивление R.

Возможные типы автоколебаний не исчерпываются рассмот­ренными примерами. Форма колебаний не обязательно бывает синусоидальной или пилообразной — она может быть какой угодно. Это относится не только к автоколебаниям, но и ко всем колебаниям вообще, включая и собственные, и вынужденные. ▲

Приведите известные вам примеры релаксационных колебаний.

Сравните релаксационные колебания с автоколебаниями в системах, со­держащих резонаторы, с точки зрения энергии, поступающей в систему за период. Покажите, что в релаксационных колебаниях поступающая за пе­риод энергия сравнима (одного порядка) с полной энергией колебаний.

• Если период колебаний в системе с резонатором определяется параметрами этого резонатора, то какими факторами определяется период релаксацион­ных колебаний?