§ 26. Вынужденные колебания в контуре. Резонанс

Выше рассматривались электромагнитные колебания в контуре, происходящие в отсутствие внешних воздействий. Внешнее воздей­ствие сводилось лишь к сообщению некоторого начального заряда конденсатору, после чего система предоставлялась самой себе. Такое внешнее воздействие отражалось не в дифференциальном уравне­нии колебаний, а лишь в начальных условиях к нему. В реальных системах эти собственные колебания всегда затухают.

Вынужденными электромагнитными колебаниями, как и в ме­ханике, называют колебания в электрических цепях, происходящие при постоянно присутствующем внешнем воздействии.

U- IVqCOS 0)t

r

-1 1_

Уравнение вынужденных колебаний в контуре. Рассмотрим RLC-контур, изображенный на рис. 165. Будем считать, что к нему при­ложено синусоидальное внешнее напряжение /7(г) = /7₀ cos шг, частота ш которого в общем случае не совпадает с частотой ш₀ собственных колебаний в этом контуре. В последовательной цепи в каждый момент времени напряжение /7(0 равно сумме напряжений на отдельных элементах цепи:

U_L+U_R + U_C = /7(0- (1) _Рис. ₁₆₅. последова-

тельный iJLC-контур

Считая, что при выполнении условий квази­стационарности сила тока / в один и тот же момент времени во всех участках контура одинакова, можем подставить в (1) /7_С = qlС, U_R = IR и U_L = Ll = L'q:

L'q+ Rq + q/C = U₀ cos шг. (2)

Вводя такие же обозначения, как и при изучении собственных колебаний:

ш²₀=1/ЬС, 2у = R/L, f₀=U₀IL, (3)

перепишем уравнение (2) в виде

q + 2yq + <£>lq = /₀ cos Ш. (4)

Уравнение (4) для заряда конденсатора q(t) имеет точно такой же вид, что и уравнение вынужденных колебаний механического осциллятора с собственной частотой ш₀ и затуханием 7, происходя­щих под действием синусоидальной внешней силы:

х + 2ух + Шц-х = /₀ cos Ш, /₀ = Fjm.

Установившиеся колебания в контуре. Предыдущее утверждение означает, что вынужденные колебания заряда конденсатора проис­ходят точно так же, как и вынужденные колебания механического осциллятора. Как и в механических системах, в колебательном кон­туре под действием синусоидального приложенного напряжения в конце концов устанавливаются колебания, которые также происхо­дят по синусоидальному закону на частоте приложенного напряже­ния ш, с некоторой постоянной амплитудой и некоторым сдвигом по фазе относительно приложенного напряжения. Такие колебания на­зываются установившимися.

Все характеристики установившихся колебаний заряда конденса­тора q(t) (т. е. амплитуду и сдвиг по фазе) можно найти, как и в механике, методом векторных диаграмм. Однако в этом нет необхо­димости. Мы уже рассматривали в § 22 при изучении переменного тока процессы в цепи, показанной на рис. 165, и нашли характер изменения силы тока /(г) под действием приложенного напряжения U(t) = U₀ cos со* в режиме установившихся колебаний:

/(r) = /₀cos(a>i-<p), (5)

о

и,

(6)

⁰ vV-HcoL-l/coC)²'

tg у.

coZ.-1/соС (7)

Выражения (5)—(7) дают установившееся решение дифференциаль­ного уравнения для силы тока. Это уравнение можно получить из уравнения (2) почленным дифференцированием по V.

U + RI + I/C = -и₀ш sin со*. (8)

Таким образом, рассматривая в § 22 процессы в цепях синусои­дального переменного тока, мы фактически изучали установившие­ся колебания под действием синусоидального приложенного внешне­го напряжения. В частности, там были рассмотрены резонансные яв­ления в таких цепях. Когда внешнее напряжение подается на последовательно соединенные конденсатор и катушку индуктивно­сти (рис. 165), возможен резонанс напряжений, при котором, как мы видели, напряжения на реактивных элементах цепи могут пре­вышать приложенное напряжение. Когда внешнее напряжение по­дается на параллельно соединенные конденсатор и катушку (см. рис. 141), возможен резонанс токов, при котором токи в отдельных реактивных элементах могут значительно превышать ток в подводя­щих проводах.

Резонансный контур. Остановимся на резонансных явлениях не­сколько подробнее. В тех случаях, когда электрическая цепь содер­жит однотипные реактивные элементы (только конденсаторы или только катушки), в ней может запасаться энергия одного вида — только электрическая или только магнитная. Никаких собственных колебаний в таких случаях быть не может. Вынужденные колебания (переменный ток) в таких цепях, разумеется, возможны, но ника­ких резонансных явлений быть не может.

Резонансные явления происходят только в цепях, где возможны собственные колебания. Резонанс наступает, когда частота со внеш­него синусоидального воздействия приближается к собственной час­тоте со₀ = 1/VLC.

Рассмотрим для определенности резонанс в последовательном контуре (см. рис. 165). В отличие от механического осциллятора, где наибольший интерес представляло смещение x(t) из положения рав­новесия (которое является аналогом заряда конденсатора g(t)), в электрической цепи больший интерес представляет сила тока 1(f), которая является аналогом скорости x(t) механического осциллятора.

Резонансные кривые. Рассмотрим зависимость амплитуды /₀ устано­вившегося тока от частоты со приложенного напряжения. Непосредст­венно из формулы (6) видно, что амплитуда тока обращается в нуль как при со -*0, так и при со—»<»', и достигает максимального значения при обращении в нуль выражения в скобках в формуле (6), что соот­ветствует точному совпадению частоты приложенного напряжения с собственной частотой:

coL- 1/(соС) =0,

откуда

со² = 1/(LC) = со². О

Из формулы (7) видно, что при резонансе, когда со = со₀, отсут­ствует сдвиг фазы ip между приложенным напряжением и током. Выражаемые формулами (6) и (7) зависимости амплитуды устано­вившегося тока и сдвига фазы от со показаны на рис. 166.

Зависимость амплитуды заряда конденсатора от частоты прило­женного напряжения также имеет резонансный характер. Резонанс-

Рис. 166. Амплитуда силы тока и р_Ис. 167. Зависимость амплитуды заряда при

сдвиг фазы при установившихся вы- установившихся вынужденных колебаниях от

нужденных колебаниях в последова- частоты приложенного напряжения тельном /tLC-контуре

ная кривая для заряда в общих чертах похожа на резонансную кривую для тока, но отличается от нее в некоторых отношениях (рис. 167). Во-первых, максимум амплитуды, даваемый формулой

а /О

приходится на частоту

%e3 = ^0-V, (11)

где /₀ и у определяются формулами (3). Резонансная частота со_рез оказывается меньше частоты свободных колебаний в контуре. При слабом затухании, когда y«w₀, можно считать, что резонансная частота для заряда практически совпадает с со₀. При стремлении ча­стоты приложенного напряжения к нулю, т.е. при со<зссо₀, ампли­туда q_m = /(/со§, что при подстановке значений /₀ и со₀ дает CU₀, как это и должно быть.

Амплитуду вынужденных колебаний заряда в резонансе о_рез на-

ходим, подставляя частоту со_рез из (11) в выражение (10):

«рез

/о _ /о

2у Vcog-27^{2 2}У<»0 "oR-

(12)

Амплитуда колебаний заряда в резонансе тем больше, чем меньше затухание у. Вблизи резонанса затуханием пренебрегать нельзя, как бы мало оно ни было: только при учете затухания амплитуда в ре­зонансе получается конечной. Интересно сравнить значение д_т в ре­зонансе с зарядом q = CU₀ при постоянном приложенном напряже­нии U₀. Составляя отношение о_рез к CU₀, получаем

CU_Q 2у R ШойС"

(13)

Если подставить в (13) со₀ = 2к/Т и учесть, что 1/у = х есть вре­мя жизни собственных затухающих колебаний в данном контуре, то отношение q_ptJ/(CU₀) можно представить в виде

си₀ ^к т

(14)

Но х/Т есть число собственных колебаний, совершающихся в кон­туре за время жизни колебаний х. Таким образом, резонансные свой­ства /<ХС-контура характеризуются тем же параметром (добротно­стью контура), что и собственные затухающие колебания в нем.

Энергетические превращения при вынужденных колебаниях.

Чем сильнее выражены резонансные свойства контура, тем большую энергию колебаний запасает он при резонансном внешнем воздейст­вии. Естественно, что для достижения установившегося режима в этом случае требуется большее время, чем для установления коле­баний при частотах, далеких от резонансной. Если после установле­ния резонансных колебаний прекратить внешнее воздействие, коле­бания в контуре будут затухать с превращением электромагнитной энергии колебаний в джоулеву теплоту, выделяющуюся на сопро­тивлении R. Такой процесс займет столько же времени, сколько требовалось на «раскачку» контура, т. е. на достижение установив­шегося режима.

• Поясните вывод уравнения (2) для вынужденных колебаний заряда кон­денсатора колебательного контура.

• Что такое установившиеся вынужденные колебания?

• Получите выражение для амплитуды и сдвига фазы установившихся вынужденных колебаний заряда конденсатора, решая уравнение (4) ме­тодом векторных диаграмм. Покажите, что эти выражения согласуются с формулами (6) и (7) для соответствующих величин, характеризую­щих колебания силы тока в цепи.

• Объясните, почему резонансные явления возможны только в электри­ческих цепях, содержащих оба вида реактивных элементов, т. е. и кон­денсаторы, и катушки индуктивности.

• С помощью метода векторных диаграмм получите установившееся реше­ние уравнения (4) для вынужденных колебаний заряда конденсатора и покажите, что амплитуда и резонансная частота даются формулами (10) и (11). Постройте график сдвига фазы между приложенным на­пряжением и зарядом конденсатора.

• Что вы можете сказать о зависимости отношения q_pa/CU₀ (формула (13)) от частоты ш₀ собственных колебаний в контуре: это отношение пропорционально или обратно пропорционально со₀?

• Основываясь на аналогии с механическими колебаниями, покажите, что характерное время установления резонанса в колебательном контуре совпадает со временем т = 1/7 жизни затухающих собственных колеба­ний в этом контуре.

д Поглощаемая мощность. При установившихся колебаниях энергия внешнего источника расходуется лишь на их поддер­жание, т. е. на компенсацию джоулевых потерь в контуре. По­этому поглощаемая контуром мощность (равная в среднем за период колебаний подводимой к нему мощности), пропорцио­нальна квадрату амплитуды установившегося тока. Действи­тельно, записав на основании закона Джоуля—Ленца выраже­ние для мощности Р тепловых потерь

P(t) = I\t) R

и подставив в него установившееся значение силы тока I(t) из (5) и (6), получим

P(t) =llRcos (cor-45) = \llR [1 +cos2(cor-<p)],

что после усреднения по времени за период колебаний дает

P = \llR. (15)

Подставляя сюда амплитуду /₀ из (6), получим зависимость поглощаемой контуром мощности от частоты со приложенного

напряжения:

Р(ш)

2R 1₊(а>²-со²)²^²/(Ла>)²'

(16)

Как видно из (16), поглощаемая мощность максимальна при со = cog и равна Uq/(2R), как если бы все внешнее напряжение было приложено непосредственно к резистору.

Для контура с малым затуханием и, следовательно, с резко выраженными резонансными свойствами поглощаемая мощность заметно отлична от нуля лишь вблизи резонанса, т. е. при часто­тах ш, близких к собственной частоте ш₀. В этом случае удобно ввести расстройку Дш = ш — ш₀, т. е. отсчитывать частоту от ее

резонансного значения. Тогда разность квадратов в знаменателе формулы (16) можно представить в виде

ш² - o)q « 2ш₀ Дш,

Р (Дш)

после чего (16) записывается следующим образом:

ul 1

2Л 1 + (Дсо)²т²'

(17)

где т = 1/-/ = 2L/R. Форма резонансной кривой для поглощае­мой мощности /*(Дш), выражаемой формулой (17), часто встречается в физике и называется лоренцевским контуром. График этой зависимости показан на рис. 168. Он симметричен относительно оси ординат, имеет характерную колоколообраз-

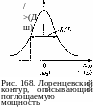ную форму. Ширина этой кривой на половине максимальной высоты может служить характеристикой ос- троты резонанса. Из формулы (17) сразу видно, что мощность умень- шается вдвое, когда второе слагае- мое в знаменателе равно единице, т. е. при расстройке

Аш=1/х = у = Я/(2Ь). Таким об­разом, ширина резонансной кривой равна 2у = R/L.

Но резонансные свойства колеба­тельного контура характеризуются, строго говоря, не абсолютным значе­нием ширины кривой, а безразмер­ным отношением резонансной частоты со₀ к ширине 2у. Эта ха­рактеристика контура очень широко используется в радиотехни­ке и называется добротностью Q:

ТЕ ■

(18)

Как видно, например, из формулы (14), эта характеристика колебательной системы уже не раз неявно фигурировала в полу­ченных нами результатах, касающихся как собственных, так и вынужденных колебаний осциллятора. ▲

• На что расходуется поступающая в колебательную систему энергия внешнего источника при установившихся колебаниях и в процессе их раскачки?

• При собственных колебаниях в контуре средние значения электри­ческой энергии конденсатора и магнитной энергии катушки равны меж­ду собой. Что можно сказать об этих средних значениях при установив­шихся вынужденных колебаниях?

• Почему при установившихся вынужденных колебаниях мощность, по­ступающая в контур от внешнего источника, равна мощности джоуле-вых потерь лишь в среднем за период, а не в каждый момент времени?

• Что такое лоренцевский контур? Какое отношение имеет он к вынужден­ным электромагнитным колебаниям?

• Что такое добротность колебательного контура? Приведите все рассмот­ренные в тексте физические эффекты, при описании которых она фи­гурировала (явно или неявно)?