§ 24. Трехфазный ток.

Электрические машины переменного тока

Наряду с простым синусоидальным переменным током в технике широко используется трехфазный ток.

Представим себе прямоугольную проволочную рамку с нескольки­ми витками, равномерно вращающуюся в однородном магнитном по­ле. Возникающая в этой рамке ЭДС индукции меняется по синусои­дальному закону. Если же вокруг общей оси вращается не одна, а три одинаковые рамки, плоскости которых повернуты относительно друг друга на 120°, то возникающие в них синусоидальные ЭДС будут сдвинуты по фазе на 120° (рис. 147):

= Ж₀ sin

if, = %_Q sin со*, Ч₂ = <?₀ sin

Обмотку каждой из этих рамок можно замкнуть на свое нагру­зочное сопротивление (рис. 148) и получить три синусоидальных переменных тока, между ко­торыми будет строго постоян­ная разность фаз. Такие три согласованных переменных тока называют трехфазным током.

Соединения звездой и тре­угольником. Так как для яв­лений в электрических цепях важны только разности по­тенциалов, то можно объеди­нить в один провод по одному

проводу из каждой цепи. В результате получается соединение гене­ратора с потребителем с помощью четырех, а не шести проводов, называемое соединением звездой (рис. 149а). Если же объединять по

Рис. 148. Три независимые линии соединения генератора с потребителями

одному проводу из каждой цепи на рис. 148 попарно, то в результа­те получается схема соединения генератора с потребителем тремя проводами, называемая соединением треугольником (рис. 1496).

В цепях трехфазного тока напряжения между концами каждой обмотки генератора называются фазными напряжениями, а токи в

а б

Рис. 149. Соединение генератора с потребителями звездой (а) и треугольником (б)

этих обмотках — фазными токами. Так же называют напряжения и токи в нагрузочных сопротивлениях. Напряжения между проводами 1, 2, 3 на рис. 149а и между любой парой проводов на рис. 1496 на­

зываются линейными напряжениями, а токи в этих проводах — ли­нейными токами. Легко видеть, что при соединении звездой фазные токи совпадают с линейными токами, а фазные и линейные напря­жения различаются. При соединении треугольником, наоборот, сов­падают фазные и линейные напряжения, а различаются фазные и линейные токи.

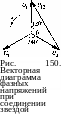Векторные диаграммы. Рассмотрим подробнее соединение звездой. Построим векторные диаграммы токов и напряжений. Предположим, что генератор разомкнут. Тогда фазные напряжения совпадают с со­ответствующими ЭДС, и поскольку последние сдвинуты по фазе на 120° и 240°, то диаграмма фазных напряжений U_x, U₂ и U₃ имеет вид, пока­занный на рис. 150. Как видно из рис. 149а, мгно­венное значение линейного напряжения, напри­мер, между проводами / и 2 равно разности мгно­венных значений соответствующих фазных напряжений. Поэтому вектор U₁₂, изображаю­щий это напряжение, равен разности векторов Xi_x и U₂, изображающих фазные напряжения в первой и второй обмотках (рис. 150). Разумеется, вектор Ui₂ можно перенести параллельно самому себе так, чтобы его начало совпало с общим центром вращения векто­ров. Из рисунка сразу видно, что амплитуда линейного напряжения при соединении звездой в V3 раз больше амплитуды фазного. То же

Рис. 151. Векторная диа­грамма токов в соединении звездой при одинаковых на­грузках

самое относится и к действующим значениям этих напряжений. Если, например, фазное напряжение в сети 220 В, то линейное напряжение в этой же сети 380 В.

Так же просто строится векторная диаграмма токов. При одина­ковых нагрузках амплитуды токов в проводах 1,2,3 равны, а токи /_р /₂, /₃ сдвинуты по фазе на 120° и 240° (рис. 151). В нулевом про­воде в любой момент ток равен сумме токов I_v /₂ и /₃ и при сим­метричной нагрузке, как видно из рис.151, обращается в нуль. В этом случае нулевой провод можно убрать, не изменяя токов в це­пи. Если нагрузка несимметрична, то длины векторов, изображаю­щих токи /j, /₂ и /₃, будут неодинаковы. Теперь в нулевом проводе будет ток /, амплитуду и фазу которого легко найти с помощью векторной диаграммы, построение которой ясно из рис. 152.

Совершенно аналогично может быть построена векторная диа­грамма фазных токов в соединении треугольником. При симметрич­ной нагрузке с помощью векторной диаграммы можно убедиться, что амплитуды линейных токов будут в V3 раз больше, чем ампли­туды фазных токов.

Все приведенные выше результаты можно получить и аналити­чески, не используя векторных диаграмм. Для этого нужно восполь­зоваться формулами (1) и соответствующими формулами для токов.

В рассмотренных схемах и обмотки генератора, и нагрузки со­единены одинаково — либо звездой, либо треугольником. Разумеет­ся, можно употреблять и комбинированные схемы, соединяя обмот­ки генератора звездой, а нагрузки — треугольником или наоборот. В технике используются различные типы соединений в цепях трех­фазного тока, но во всех случаях предпочтительной является сим­метричная нагрузка фаз, при которой потери будут наименьшими.

Преимущество использования в технике трехфазного тока по сравнению с однофазным заключается в экономии числа проводов и идущего на их изготовление материала. Но самой замечательной особенностью трехфазного тока является то, что он позволяет очень просто создать вращающееся магнитное поле. А с помощью такого поля можно сделать простые по конструкции электродвигатели, принцип работы которых заключается в следующем.

Модель синхронного и асинхронного двигателей. Будем вращать подковообразный магнит так, как показано на рис. 153. Вместе с магнитом будет вращаться и создаваемое им магнитное поле. Если в такое поле поместить магнитную стрелку, то она, стремясь уста­новиться вдоль линий ин­дукции магнитного поля, придет во вращение в ту же сторону, в которую вращает­ся поле.

Так же будет вести себя и замкнутый виток провода (рис. 153). Вследствие изме­нения пронизывающего ВИ- • Рис. 153. Модель асинхронного двигателя ток магнитного потока при

вращении магнитного поля в витке возникает ЭДС индукции и ин­дукционный ток. На этот ток со стороны магнитного поля будет дей­ствовать сила Ампера. По закону Ленца индукционный ток в витке направлен так, что взаимодействие этого тока с магнитным полем стремится уменьшить изменение магнитного потока вследствие вра­щения магнитного поля. Поэтому рамка будет вращаться вслед за магнитным полем. В этом, разумеется, можно убедиться и иначе, если с помощью правила правой руки определить направление сил Ампера, действующих на отдельные стороны рамки.

Вместо рамки можно взять массивный металлический цилиндр или ротор в виде «беличьего колеса» (рис. 154), эквивалентного большому числу соединенных между собой проводящих рамок. При вращении магнитного поля в толще металла цилиндра также будут наводиться замкнутые индукционные токи (вихревые токи, или токи Фуко). Согласно закону Ленца взаимодействие этих токов с магнитным полем будет приводить к уменьшению относительной скорости враще­ния поля и цилиндра.

Выясним, чем отличается поведение во вра- Рис. 154. Короткозам- щающемся магнитном поле магнитной стрелки кнутыи ротор асин- _и короткозамкнутой металлической рамки. При хронного двигателя „

равномерном вращении магнитной стрелки сум­марный момент действующих на нее сил дол­жен равняться нулю. Момент сил, действующих на стрелку со сто­роны магнитного поля, зависит от угла, образованного стрелкой с вектором индукции поля. Этот момент максимален, когда стрелка перпендикулярна полю, и обращается в нуль, когда стрелка направ­лена по полю.

Если на равномерно вращающуюся стрелку никакие другие мо­менты сил не действуют, то должен быть равен нулю и момент сил, действующих на нее со стороны вращающегося магнитного поля. Следовательно, в любой момент стрелка направлена вдоль поля и вращается синхронно с ним. Если же на стрелку действует тормозящий внешний момент, то стрелка, вращаясь синхронно с полем, будет несколько отставать от него по фазе, так чтобы тор­мозящий момент уравновешивался моментом сил со стороны маг­нитного поля.

Разумеется, вместо магнитной стрелки можно взять закреплен­ный на оси постоянный магнит или электромагнит, питаемый посто­янным током. Они также будут вращаться синхронно с внешним вращающимся магнитным полем.

Несколько иначе обстоит дело в случае короткозамкнутой рам­ки или сплошного цилиндра. Индукционный ток зависит от отно­сительной скорости вращения магнитного поля и ротора. При син­хронном вращении индукционный ток отсутствует и, следователь­но, равен нулю момент сил, действующих на ротор со стороны магнитного поля. Поэтому ротор может вращаться синхронно с по­лем только тогда, когда никакие тормозящие моменты на него не действуют. При наличии тормозящего момента при равномерном вращении он должен уравновешиваться моментом сил, действую­щих на индукционные токи в роторе со стороны магнитного поля.

Для возникновения этих индукционных токов ротор должен вра­щаться медленнее магнитного поля. Таким образом, угловая ско­рость ротора меньше угловой скорости вращения магнитного поля и зависит от тормозящего момента. Чем больше тормозящий мо­мент, тем медленнее вращается ротор.

Магнитная стрелка или электромагнит постоянного тока во вра­щающемся магнитном поле — это модель синхронного двигателя переменного тока, который находит себе применение в тех случаях, когда необходимо иметь строго постоянное, не зависящее от нагруз­ки число оборотов. Короткозамкнутый ротор во вращающемся маг­нитном поле — это модель асинхронного двигателя переменного тока, угловая скорость вращения ротора которого зависит от механической нагруз­ки. В силу исключительной простоты кон­струкции и высокой надежности асинхрон­ные двигатели получили широкое распрост­ранение в технике.

Вращающееся магнитное поле. Опишем теперь способ получения вращающегося магнитного поля в электродвигателях пере­менного тока.

Предположим, что у нас есть равномер­но вращающееся против часовой стрелки в плоскости ху магнитное поле, вектор ин­дукции В которого не меняется по модулю (рис. 155). Из этого ри­сунка видно, что такое поле можно рассматривать как результат сложения двух магнитных полей, индукция одного из которых на­правлена вдоль оси х и меняется со временем по закону

B_x(t) = В cos tor, (2)

а индукция другого направлена по оси у и имеет вид B_y(t) = В sin tor = В cos tor —

(3)

т. е. отстает по фазе от В_х на л;/2. Такие поля легко получить, рас­полагая взаимно перпендикулярно две одинаковые катушки и про­пуская по ним синусоидальные токи одинаковой амплитуды, но сдвинутые по фазе на л/2. Сумма этих полей и дает вращающееся магнитное поле.

Совершенно аналогично можно получить вращающееся магнит­ное поле с помощью трехфазного переменного тока. Для этого нужно три одинаковые катушки расположить так, чтобы их оси лежали под углом 120° друг к другу и пересекались в одной точке, и включить катушки в сеть трехфазного тока по схеме звезды или треугольника. Тогда магнитное поле, создаваемое каждой катушкой, будет направлено вдоль оси соответствующей катушки и зависеть от времени в соответствии с формулами (1):

Bj(0 = В₀₁ sin со*,

B₂(0 = Bo₂sin fat - , B₃(0=B₀₃sin|co<-^j.

(4)

Амплитудные значения этих полей В₀₁, В₀₁ и В₀₃ равны между собой. Обозначим их через В₀. Результирующее поле

в(0 = в,(0+в₂(0 + в₃(0 (5)

имеет постоянный модуль, равный (3/2)В₀, и равномерно вращается в плоскости осей катушек с угловой скоростью со. Чтобы убедиться в этом, спроецируем вектор индукции результирующего поля В на оси х и у (рис. 156):

В_х = В₂ cos 30° - В_ъ cos 30° = ^В₀ j^sin fait - Щ - sin (a>t -Используя формулу разности синусов двух углов, получаем

B_x = -B_Q cos со*.

(6)

Аналогично,

В_у = В_{- В₂ cos 30° - В₃ cos 30° =

= В_п

sin co<-i_Sin -^sin (со<-^)].

Преобразуя второе и третье слагаемые в квадратных скобках с по­мощью формулы суммы синусов, найдем

В_у = | В₀ sin со*. (^?)

Сравнивая (6) и (7) с формулами (2) и (3), убеждаемся, что поле В действительно равномерно вращается с угловой скоростью со. Направление вращения магнитного поля, а следовательно, и ротора электродвигателя, можно изменить на противоположное, если поменять местами концы любой пары прово­дов, присоединенных к катушкам статора, со­здающим магнитное поле.

Отметим, что синхронные электродвигате­ли переменного тока являются обратимыми, т. е. могут быть использованы и как генерато­ры. Если не подавать напряжение на обмотки статора, а ротор (электромагнит) привести во вращение, то в обмот­ках статора будет индуцироваться переменное трехфазное, напряже­

ние. А асинхронный двигатель подобен трансформатору, у которого вторичная обмотка выполнена подвижной. Что же касается физиче­ской сущности явлений, то в обоих случаях она одинакова, посколь­ку токи и во вторичной обмотке трансформатора, и в роторе асинх­ронного двигателя имеют чисто индукционное происхождение.

• Что такое трехфазный переменный ток?

• Постройте векторные диаграммы при соединении треугольником. Пока­жите, что при симметричной нагрузке амплитуды линейных токов будут в vT раз больше, чем амплитуды фазных токов.

• Почему в сетях трехфазного тока всегда стремятся нагрузить все три фазы по возможности одинаково?

• Какими преимуществами обладает трехфазный ток перед однофазным?

• Объясните принцип действия синхронного и асинхронного электродви­гателей. Почему угловая скорость вращения ротора асинхронного двига­теля уменьшается с увеличением механической нагрузки?

• Почему синхронные двигатели переменного тока обратимы, а асинхрон­ные — нет?

• Какими способами можно создать вращающееся магнитное поле?