§13. Расчет цепей постоянного тока

Расчет электрических цепей заключается в определении сил токов во всех ветвях и напряжений на всех элементах. Когда цепь содержит один источник тока, ее расчет не представляет принципиальных трудностей, поскольку всю нагрузку, какой бы разветвленной она ни была, можно заменить одним эквивалентным сопротивлением.

Как пример такого рода расчетов рассмотрим следующую задачу.

Задача

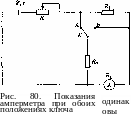
В цепи, схема которой показана на рис. 80, подбором переменного сопро­тивления добиваются, чтобы показания амперметра были одинаковыми неза­висимо от того, в каком положении, А или В, находится ключ К. Чему равно

внутреннее сопротивление ис­точника тока, если этого удалось добиться при значениях пере­менного сопротивления и сопро­тивления амперметра, равных соответственно R и Я_а?

Решение Фактически в этой задаче речь идет о двух раз­ных цепях, в которых показания прибора оказались одинаковы­ми. Прямой путь ее решения за­ключается в расчете для каждой схемы силы тока в соответствую­щем ответвлении, содержащем амперметр. При этом в каждом случае придется сначала найти эквивалентное сопротивление нагрузки, определить силу тока в неразветвлен-ной части цепи, а затем найти силу тока через амперметр.

В данном случае, как и во многих других, можно обойтись без расчета эк­вивалентного сопротивления и найти ответы на поставленные в условии вопро­сы, используя несколько раз закон Ома для участка цепи и тот факт, что ЭДС равна сумме напряжений на всех участках любого контура, по которому мож­но обойти рассматриваемую замкнутую цепь.

Рассмотрим сначала схему, соответствующую ключу К в положении А. В этом случае R_x и амперметр соединены последовательно, а параллельно их об­щему сопротивлению Я, + R_a включено R₂. Обозначив через / силу тока в ам­перметре (одинаковую в обоих случаях), а через/' —в сопротивленииR₂, имеем

1_ Г

Я,

Сила тока в неразветвленной части цепи равна сумме /и/'. Учитывая это, можно при обходе всей замкнутой цепи по контуру, содержащему амперметр, написать

# = /(Я_а-г-Я,) + /

(R + r).

Аналогично, рассматривая схему, соответствующую ключу К в положе­нии В, придем к равенствам

I" R.-

где I" — сила тока в сопротивлении R₂ при таком положении ключа, и

sf = //?. + /|l +?gj(R+r + R_l).

Приравнивая получившиеся выражения для ЭДС источника, после приве­дения подобных членов при R_x * 0 получаем

г + R = Л_а

— сопротивление источника вместе с включенным последовательно с ним сопротивлением R должно быть равно сопротивлению амперметра Л_а, чтобы его показания в обоих случаях были одинаковы. Интересно отметить, что это условие не зависит от значений сопротивлений R_x и R₂. Однако ясно, что ни R_v ни R₂ при этом не должны быть равны нулю: при R_x = 0 обе схемы не различаются, а при R₂ = 0 показания амперметра равны нулю при любых значениях всех остальных параметров.

Рассмотрим цепи, содержащие несколько источников тока. На практике особенно важны случаи, когда одинаковые источники со­единяются в батареи.

Последовательное соединение источников тока. При после- довательном соединении нескольких источников (рис. 81) правила действий нам фактически уже известны. В соответствии с формулой (4) § 12 сила тока определяется отношением суммы ЭДС всех соеди- ненных источников тока к сумме сопротив- лений всех последовательных элементов це- % г % г % г пи, включая нагрузку:

у_{1 +} у₂ + ...+у,

r_{l +} r₂ + ...+r_n + R- ^У >

_R_

-TZZb

Когда все п источников одинаковы, формула (1)принимает вид

nr+R' ^ ' Рис.81. Последовательное

соединение источников тока

Такая батарея источников тока эквивалент­на одному источнику, как ЭДС, так и внут­реннее сопротивление которого в п раз больше, чем у одного элемента батареи. Последовательное соединение элементов позволяет получить источник с высоким напряжением. Однако при этом возрастает внут­реннее сопротивление. Чтобы такое соединение привело к увеличению тока в нагрузке по сравнению с источником из одного элемента, необ­ходимо выполнение условия nr<szR. При этом из (2) следует, что I « ri&IR — ток от батареи возрастает примерно в п раз.

Параллельное соединение источников тока. Перейдем к парал­лельному соединению одинаковых элементов в батарею (рис.82). Ток / через нагрузку, т. е. в неразветвленной части цепи, равен сумме токов во всех элементах батареи. Так как все элементы оди­наковы, то из симметрии ясно, что и токи в них одинаковы и равны 1/п. Вся батарея может быть заменена одним эквивалентным источ­ником тока с ЭДС <f, такой же, как и у одного элемента, и внут­ренним сопротивлением r/п. Поэтому выражение для тока / в на­грузке имеет вид

^{/ =} тга- (3)

Несмотря на то, что параллельное соединение источников не приводит к увеличению ЭДС, его целесообразно применять в тех случаях, когда требуется получить источник тока с малым внутрен­ним сопротивлением. Такое соединение элементов приведет к увеличению тока в нагрузке почти в п раз, если й«г.

Отметим, что при R = г оба способа соединения источников дают одинаковый результат для тока в нагрузке, приводя к его увеличению в 2п/(п + 1) раз.

Возможно и комбинированное (сме­шанное) соединение элементов в бата­рею, при котором включаются парал­лельно т групп, в каждой из которых имеется п последовательно соединенных элементов. Такая батарея эквивалентна одному источнику, ЭДС которого в п раз больше, чем у одного элемента, а внут­реннее сопротивление равно (п/т)г.

Параллельное и смешанное соедине­ния разных источников тока используют­ся очень редко. Такие цепи могут быть рассчитаны с помощью правил Кирхго­фа, которые пригодны для расчета лю­бых сложных разветвленных цепей.

Всегда ли нужен второй источних? Ос­тановимся на анализе условий работы последовательно соединенных разных ис­точников тока. Для этого рассмотрим цепь, схема которой показана на рис. 83. Выясним, всегда ли наличие второго ис­точника с ЭДС <f₂ приводит к увеличе­нию тока в цепи, первоначально содержащей только один источ­ник с ЭДС Очевидно, что второй источник имеет смысл под­

ключать, только если

r_l + r₂ + R

r,+R'

(4)

Умножая обе части этого неравенства на положительную величину (/■, + r₂ + R) (/■, + R) и приводя подобные члены, получаем

%₂(r_l + R) > 5?,г.

откуда

г, +R'

(5)

Смысл неравенства (5) очевиден: в соответствии с формулой (7) §12 слева стоит ток короткого замыкания второго источника, а справа — ток в цепи, содержащей только первый источник. Поэто­му последовательное подсоединение второго источника целесообраз­но только в том случае, когда ток его короткого замыкания больше тока в цепи, в которую мы собираемся его включить. Практически в уже собранной цепи обнаружить «бесполезный» источник можно с помощью вольтметра, поочередно подключая его к клеммам каждо­го из источников.

• Как найти силу тока в любом ответвлении цепи, содержащей только один источник тока?

• В каких случаях целесообразно последовательное соединение одинако­вых источников тока в батарею, а в каких — параллельное?

• При каком условии последовательное подключение еще одного источни­ка тока не приведет к увеличению тока в той же нагрузке?

• Объясните, как с помощью вольтметра можно обнаружить «бесполез­ный» источник в уже собранной последовательной батарее элементов.

д Правила Кирхгофа. Рассмотрим произвольную разветвлен­ную цепь, часть которой изображена на рис. 83. Первое правило Кирхгофа относится к узлам, т. е. точкам, в которых сходится не менее трех проводников. Как уже отмечалось, вследствие закона сохранения заряда в любой точке цепи, в том числе и в любом узле, при прохождении постоянного тока не должно происходить накопления электрического заряда. Поэтому сумма притекаю­щих к узлу токов должна равняться сумме вытекающих. Если условиться считать подходящие к узлу токи положительными, а исходящие из узла — отрицательными, то можно сказать, что алгебраическая сумма сил токов в узле равна нулю:

п

2h = o,

где п обозначает число проводов, сходящихся в узле.

Второе правило Кирхгофа относится к произвольным замкну­тым контурам, которые можно мысленно выделить в рассматрива­емой разветвленной цепи. Рассмотрим контур АБСА на рис. 84. Поскольку при расчете мы будем использовать закон Ома для нео-

Рис. 84. Часть разветвленной электрической цепи

днородного участка цепи, то, как мы видели, направление токов в неразветвленных участках можно задать произвольно, например так, как на рис. 84. (Напомним, что если в результате расчета ка­кой-либо из токов окажется отрицательным, то это означает, что в действительности ток на этом участке течет в противоположную сторону.) Запишем закон Ома для каждого из неразветвленных участков контура АБСА. Обозначив потенциалы узлов через <р_А, «Рд и <р_с, получим

¹2^R2 = Ч>В — Ч>С ^- ^2> (⁷)

I₃R₃ = <р_с - <Рл + ^з-

В этих формулах через R_k обозначено полное сопротивление участка, по которому течет ток 1_к. Легко заметить, что если пер­вое уравнение системы (7) умножить на —1 и затем сложить по­членно все три уравнения, то потенциалы узлов выпадают:

— J\R{ "Г* ^2^R2 ^3^R3 ⁼ — — *^3* (^

Глядя на формулу (8), нетрудно сформулировать правило, с помощью которого можно было бы непосредственно получить это равенство: нужно выбрать определенное направление обхода зам­кнутого контура (например, по часовой стрелке) и приравнять ал­гебраическую сумму произведений сил токов на сопротивления со­ответствующих участков алгебраической сумме ЭДС, встречаю­щихся в этом контуре. При этом ток считается положительным,

если его направление совпадает с направлением обхода контура, и отрицательным в противоположном случае; ЭДС берется со зна­ком « + », если она повышает потенциал в цепи в направлении об­хода контура, и со знаком «—», если понижает. Это и есть второе правило Кирхгофа, которое можно коротко записать так:

а т

2l_kR_t = 2*i> (9)

*=i /-1

где л — число неразветвленных участков в рассматриваемом контуре (совпадающее с числом встречающихся в этом контуре узлов), am — число источников ЭДС, действующих в контуре.

Правила расчета сложных цепей. Теперь можно сформулиро­вать общие правила расчета произвольных разветвленных цепей постоянного тока.

1. 

   Обозначить на схеме токи во всех неразветвленных участ­ках, произвольно задавая им направление.

2. Согласно первому правилу Кирхгофа написать уравнения (6) для всех узлов, кроме одного (уравнение для последнего узла писать не нужно, так как оно является следствием предыдущих).

3. Согласно второму правилу Кирхгофа составить уравнения (9) для всех простых контуров, которые можно выделить в данной цепи и которые не получаются наложением уже рассмотренных. Простым считается такой контур, при обходе которого мы побыва­ем в каждой точке только по.одному разу. В правильно выбранной системе контуров каждый участок цепи должен фигурировать по крайней мере в одном из контуров.

4. Если в результате решения полу­чившейся системы уравнений какие-либо токи окажутся отрицательными, то в действительности их направление проти­воположно выбранному на схеме.

Пример расчета. Для иллюстрации применения правил Кирхгофа рассмот- рим условия работы батареи из двух разных параллельно соединенных источ- ников. Параметры схемы указаны на dhc 85 ^Рис' ^к У^{СЛОВУ1ЯМ} работы

" U - " источников тока при парал-