11 При последовательном соедине-

Рис. 45. Последовательное соедине- нии предварительно незаряженных ние конденсаторов конденсаторов (рис. 45) заряды q на

. всех конденсаторах одинаковы, а полное напряжение U равно сумме напряжений U_t на отдельных кон­денсаторах:

С другой стороны, рассматривая батарею как один конденсатор, имеем

= (12)

Сравнивая (11) и (12), видим, что при последовательном соедине­нии конденсаторов складываются обратные емкостям величины:

^xc=k⁺k⁺-⁺h ⁽¹³⁾

При последовательном соединении емкость батареи меньше самой малой из емкостей соединенных конденсаторов.

• В каком случае два проводящих тела образуют конденсатор?

• Что называется зарядом конденсатора?

• Как установить связь между единицами емкости СИ и СГСЭ?

• Объясните качественно, почему емкость конденсатора увеличивается при уменьшении зазора между обкладками.

• Получите формулу для емкости плоского конденсатора, рассматривая электрическое поле в нем как суперпозицию полей, создаваемых двумя плоскостями, заряженными разноименно.

• Получите формулу для емкости плоского конденсатора, рассматривая его как предельный случай сферического конденсатора, у которого R_x и R₂ стремятся к бесконечности так, что разность R_l — R₂ = d остается постоянной.

• Почему нельзя говорить о емкости уединенной бесконечной плоской пластины или отдельного бесконечно длинного цилиндра?

Охарактеризуйте кратко различие между феноменологическим и микро­скопическим подходами при исследовании свойств вещества в электри­ческом поле.

Каков смысл диэлектрической проницаемости вещества?

Почему при расчете емкости батареи последовательно соединенных кон­денсаторов оговаривалось условие, чтобы они предварительно не были заряжены?

В чем смысл последовательного соединения конденсаторов, если оно приводит лишь к уменьшению емкости?

д Поле внутри и вне конденсатора. Чтобы подчеркнуть разли­чие между тем, что называют зарядом конденсатора, и полным за­рядом обкладок, рассмотрим следующий пример. Пусть наружная обкладка сферического конденсатора заземле­на, а внутренней сооб­щен заряд q. Весь этот заряд равномерно рас­пределится по внешней поверхности внутрен­ней обкладки. Тогда на внутренней поверх­ности наружной сферы индуцируется заряд —q, и, следовательно, заряд конденсатора ра­вен q. А что будет на внешней поверхности

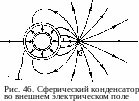
наружной сферы? Это зависит от того, что окружает конденсатор. Пусть, например, на расстоянии / от поверхности внешней сферы находится точечный заряд Q (рис. 46). Этот заряд никак не повли­яет на электрическое состояние внутреннего пространства конден­сатора, т. е. на поле между его обкладками. В самом деле, внутрен­нее и внешнее пространства разделены толщей металла наружной обкладки, в которой электрическое поле равно нулю.

Заряд на внешней поверхности обкладки. Но характер поля во внешнем пространстве и заряд, индуцированный на наруж­ной поверхности внешней сферы, зависят от величины и по­ложения заряда Q. Это поле будет точно таким же, как и в случае, когда заряд Q находится на расстоянии / от поверх­ности сплошного заземленного металлического шара, радиус ко­торого равен радиусу внешней сферы конденсатора (рис. 47). Таким же будет и индуцированный заряд.

Для нахождения величины индуцированного заряда будем рассуждать следующим образом. Электрическое поле в любой точке пространства создается зарядом Q и зарядом, индуциро­

ванным на поверхности шара, который распределен там, разуме­ется, неравномерно — как раз так, чтобы обратилась в нуль ре­зультирующая напря­женность поля внутри шара. Согласно прин­ципу суперпозиции по­тенциал в любой точке можно искать в виде суммы потенциалов полей, создаваемых то­чечным зарядом q и точечными зарядами, на которые можно раз­бить распределенный по поверхности шара индуцированный за­ряд. Поскольку все элементарные заряды Aq_t, на которые разбит индуцированный на поверхности шара заряд Q', находятся на одинаковом расстоянии R от центра шара, то потенциал создава­емого им поля в центре шара будет равен

Тогда полный потенциал в центре заземленного шара равен Ч>о-*(£ + А)=⁰'

откуда

Знак минус отражает тот факт, что индуцированный заряд всег­да противоположного знака.

Итак, мы видим, что заряд на наружной поверхности внешней сферы конденсатора определяется тем окружением, в котором на­ходится конденсатор, и не имеет никакого отношения к заряду конденсатора q. Полный заряд внешней обкладки конденсатора, разумеется, равен сумме зарядов ее внешней и внутренней по­верхностей, однако заряд конденсатора определяется только заря­дом внутренней поверхности этой обкладки, который связан сило­выми линиями поля с зарядом внутренней обкладки.

В разобранном примере независимость электрического поля в пространстве между обкладками конденсатора и, следовательно, его емкости от внешних тел (как заряженных, так и незаряжен­ных) обусловлена электростатической защитой, т. е. толщей металла внешней обкладки. К чему может привести отсутствие такой защиты, можно увидеть на следующем примере.

Плоский конденсатор с экраном. Рассмотрим плоский конден­сатор в виде двух параллельных металлических пластин, элект­рическое поле которого практически целиком сосредоточено в пространстве между пластинами. Заключим конденсатор в неза­ряженную плоскую металлическую коробку, как показано на рис. 48. На первый взгляд может показаться, что картина поля между обкладками конденсатора не изменится, так как все поле сосредоточено между пластинами, а краевым эффектом мы пре­небрегаем. Однако легко видеть, что это не так. Снаружи кон­денсатора напряженность поля равна нулю, поэтому во всех точ­ках слева от конденсатора потенциал одинаков и совпадает с по­тенциалом левой пластины. Точно так же потенциал любой точки справа от конденсатора совпадает с потенциалом правой пластины (рис. 49). Поэтому, заключая конденсатор в металли­ческую коробку, мы соединяем проводником точки, имеющие разный потенциал.

В результате в металлической коробке будет происходить пере­распределение зарядов до тех пор, пока не выравняются потенци­алы всех ее точек. На внутренней поверхности коробки индуциру­ются заряды, и появится электрическое поле внутри коробки, т. е. снаружи конденсатора (рис. 50). Но это означает, что на внешних

		1
	V	и	\
	1

Рис. 48. Конденсатор Рис. 49. Электрическое в металлической ко- поле заряженного плос- робке кого конденсатора

поверхностях пластин конденсатора тоже появятся заряды. Так как при этом полный заряд изолированной пластины не меняется, то заряд на ее внешней поверхности может возникнуть только за счет перетекания заряда с внутренней поверхности. Но при изме­нении заряда на внутренних поверхностях обкладок изменится на­пряженность поля между пластинами конденсатора.

Таким образом, заключение рассмотренного конденсатора в металлическую коробку приводит к изменению электрического состояния внутреннего пространства.

Изменение зарядов пластин и электрического поля в этом примере может быть легко рассчитано. Обозначим заряд изоли­рованного конденсатора через д. Заряд, перетекающий на наруж­ные поверхности пластин при надевании коробки, обозначим че­рез д'. Такой же заряд противоположного знака будет индуциро­ван на внутренних поверхностях коробки. На внутренних поверхностях пластин конденсатора останется заряд д — д'. Тогда в пространстве между пластинами напряженность однородного поля будет равна (g — g')/(St₀) в единицах СИ, а вне конденса­тора поле направлено в противоположную сторону и его напря­женность равна g'/(St₀), где S — площадь пластины. Требуя, чтобы разность потенциалов между противоположными стенками металлической коробки была равна нулю, и считая для простоты расстояния между всеми пластинами одинаковыми и равными d (рис.50), получаем

_{~f d + i^-d-f d = 0,}

ЛСо StQ StQ

откуда д' = д/3. Это значит, что напряженность поля в конден­саторе составляет теперь 2/3 первоначального значения, а вне

с

Рис. 51. Переход к эквивалентной схеме для конденсатора в металлической коробке

конденсатора поле в три раза слабее, чем было в конденсаторе до надевания коробки. Разность потенциалов между обкладками конденсатора £/₍ составляет 2/3 первоначального напряжения на конденсаторе U.

Емкость изолированного конденсатора есть С = g/U. Если под емкостью системы, получившейся при надевании на конденсатор металлической коробки, понимать отношение полного заряда д, сообщенного пластине, к разности потенциалов между пластина­ми U_v то

С =^- = -С ^Li u_v г^L"

Этот результат легко понять, если учесть, что после надевания коробки поле существует во всех трех промежутках между пла­стинами, т. е. фактически имеются три одинаковых конденсато­ра, эквивалентная схема включения которых показана на рис. 51. Вычисляя емкость получившейся системы конденсаторов, полу­чаем С, = (3/2) С.

Надетая на конденсатор металлическая коробка осуществляет электростатическую защиту системы. Теперь мы можем под­носить снаружи к коробке любые заряженные или незаряженные тела и при этом электрическое поле внутри коробки не изменит­ся. Значит, не изменится и емкость системы.

Обратим внимание на то, что в разобранном примере, выяс­нив все, что нас интересовало, мы тем не менее обошли стороной вопрос о том, какие же силы осуществили перераспределение за­рядов. Какое электрическое поле вызвало движение электронов в материале проводящей коробки?

Очевидно, что это может быть только то неоднородное поле, которое выходит за пределы конденсатора вблизи краев пласти­ны (см. рис.39). Хотя напряженность этого поля мала и не принимается во внимание при расчете изменения емкости, именно она определяет суть рассматриваемого явления — пере­мещает заряды и этим вызывает изменение напряженности электрического поля внутри коробки. ▲

• Почему под зарядом конденсатора следует понимать не полный заряд обкладки, а только ту его часть, что находится на ее внутренней сторо­не, обращенной к другой обкладке?

• В чем проявляется роль краевых эффектов при рассмотрении электро­статических явлений в конденсаторе?

• Как изменится емкость батареи конденсаторов, если замкнуть между со­бой обкладки одного из них?