5 5. Расчет электрических полей

^эасчеты электрических полей, создаваемых заданным распределе-шем зарядов, основаны на использовании принципа суперпозиции. Эти расчеты существенно упрощаются при наличии какой-либо

симметрии в распределении создающих поле зарядов. Рассмотрим примеры таких расчетов в конкретных задачах.

Задачи

1. Поле заряженного шара. Шар радиуса r равномерно заряжен по объ­ему. Полный заряд шара q. Найти напряженность и потенциал электри­ческого поля, создаваемого таким шаром.

Решение. Так как распределение создающих поле зарядов сфериче­ски-симметрично, то и создаваемое ими электростатическое поле должно об­ладать такой же симметрией. Это значит, что потенциал и модуль напря­женности зависят только от расстояния г до центра заряженного шара, а вектор напряженности во всех точках имеет радиальное направление. Однако зависимость от г величин <р(г) и Е{г) будет разной для внешней (г > R) и внутренней (г < R) областей.

Симметрия системы позволяет применить теорему Гаусса для расчета на­пряженности поля Е{г). Для области г > R этот расчет ничем не отличается от описанного в предыдущем параграфе расчета напряженности поля шара, рав­номерно заряженного по поверхности. Напряженность поля и, следовательно, потенциал, оказываются точно такими же, как у точечного заряда q, помещен­ного в центр шара:

Е(г)=к^, <р(0 =*7 (r>R). (1)

Для нахождения напряженности поля внутри шара рассмотрим поток на­пряженности через сферическую поверхность радиуса г < R, концентриче­скую с шаром. Поскольку силовые линии всюду пересекают эту поверхность под прямым углом, то поток N вектора Е через нее равен Е{г)Лпг². По теореме Гаусса этот же поток пропорционален полному заряду q', находящемуся внут­ри сферы: N = Ankq'. При постоянной плотности заряд пропорционален объе­му, т.е. q' = qrⁱ/Rⁱ. Поэтому N — 4nkqr³/R³. Приравнивая эти выражения для потока, имеем

Е-4пг² = 4лк

откуда

(2)

Видно, что напряженность поля внутри равномерно заряженного шара пропорциональна расстоянию г от его центра. На поверхности шара, т.е. при г — R, значения напряженности поля Е(г), даваемые формулами (1) и (2), совпадают.

Потенциал <р(г) для внутренней точки может быть найден как работа сил поля при перемещении единичного заряда из этой точки в бесконечность. Фак­тически требуется вычислить только работу при перемещении до поверх­ности, так как работа при перемещении от поверхности в бесконечность равна значению потенциала на поверхности шара: <р(г) = kqIR. При линейной зави­симости силы от расстояния в (2) работа при перемещении из данной точки, находящейся на расстоянии г от центра шара, до поверхности равна

Таким образом, при г < R потенциал имеет вид

(3)

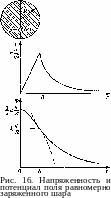Графики Е(г) и ip(r) показаны на рис. 16. Оба графика непрерывны, од­нако при г = R на графике напряженности имеется излом, в то время как на графике потенциала парабола (3) при г < R плавно переходит в гиперболу (1) при г > R. Одинаковый наклон каса­тельных к параболе и гиперболе при г = R легко объяснить, если вспомнить о связи напряженности и потенциала: непрерывность наклона касательной к графику <р(г) следует из непрерывно­сти Е(г).

2. Неустойчивость равновесия за­рядов. Заряды q\ и qz = — qi/2 за­креплены на расстоянии / друг от дру­га. В какой точке создаваемого ими по­ля будет находиться в равновесии пробный заряд? Устойчиво ли это рав­новесие?

Решение. Очевидно, что проб­ный заряд q может быть в равновесии только тогда, когда он расположен на прямой, проходящей через заряды q\ и q₂ (рис.17). Обозначим через х рассто­яние от заряда q\ до точки равновесия. Будем для определенности считать, что заряд q_x положительный, a q₂ — отри­цательный. Показанные на рис. 17 си­лы, действующие на положительный (рис. 17а) и отрицательный (рис.176)

пробный заряд q со стороны зарядов q_x и q₂, в точке равновесия равны по модулю. Расстояние х до этой точки можно найти, приравнивая модули на-пряженностей и полей зарядов q_x и q₂:

X*

(4)

©-«1

-е-

q₂--q_x II

-®-+-

© --0 <-©-*•—

«l «₂"-«l^/2 6 ^x

Рис. 17. Равновесие положительного (а) и отрицательного (б) пробного заряда q в поле зарядов q_x и q₂= —q\l2

Учитывая, что q₂ = — <7i/2, приходим к квадратному уравнению для иско­мого расстояния х:

х² - 4/jc + 2/² = О,

откуда х = I (2 ± yfl).

Положению равновесия пробного заряда соответствует корень х = l(2±V2) » 3,41/. Второй корень соответствует положению равновесия в случае, когда q₂ = q^/2, так как уравнение (4) справедливо и при одноимен­ных зарядах q^ и q₂.

Для выяснения вопроса об устойчивости равновесия можно рассмотреть силы, действующие на пробный заряд при его небольшом смещении из поло­жения равновесия. Рассмотрим сначала смещение в направлении, перпенди-

Рис. 18. По отношению к поперечным смещениям равновесие положительного пробного заряда устойчиво, а отрицательного — неустойчиво

кулярном прямой, проходящей через q_l и q₂. Из рис. 18 видно, что на положи­тельный пробный заряд будет действовать сила (равнодействующая F\ и F₂), направленная к положению равновесия. Так получается потому, что силы F'j и F'₂ вблизи точки равновесия почти равны по модулю, но несколько отличаются по направлению. На отрицательный пробный заряд будет действовать сила (равнодействующая F'{ nF₂), направленная от положения равновесия.

Отсюда, однако, нельзя сделать вывод о том, что равновесие положительного пробного заряда будет устойчивым, а отрицательного — неустойчивым. В самом деле, если рассмотреть малые смещения из точки равновесия вдоль прямой, про­ходящей через q_lnq₂, все будет наоборот: на положительный заряд будет дейст­вовать сила, направленная от точки равновесия (рис. 19а), а на отрицатель-

е—-—е —»-

Ч\ Чг—Чх¹² а ^Х

о— в <-е->—-

Ql <?₂—<?i/2 _б ^х

Рис. 19. По отношению к продольным смещениям равновесие положительного пробного заряда неустойчиво (а), а отрицательного — устойчиво

ный — к положению равновесия (рис Л 96). Это легко понять, заметив, что при таком смещении относительное изменение расстояния до q₂ больше, чемдо^.

Таким образом, в электростатическом поле двух точечных зарядов равно­весие пробного заряда не может быть устойчивым: всегда найдутся.такие сме­щения из положения равновесия, при которых на пробный заряд будет дейст­вовать сила, «уводящая» егодальшеот этого положения.

Подмеченное на этом примере обстоятельство имеет совершенно общий характер: невозможно устойчивое равновесие заряда под действием только электростатических сил.

Устойчивое равновесие в потенциальном поле соответствует минимуму по­тенциальной энергии. Невозможность устойчивого равновесия пробного заря­да в электростатическом поле означает, что потенциал <р (г) любого поля, кото­рый может быть представлен как сумма членов вида 1 /1г — r_{ |, где r_t — ради­ус-вектор i-ro заряда, создающего поле, не имеет минимумов и максимумов на любом конечном расстоянии.

Вопрос. Объясните, почему можно утвер­ждать, что <р(г) не может иметь не только мини­мума, но и максимума.

3. Однородное поле в полости. Докажите, что электростатическое поле внутри сфериче­ской полости в равномерно заряженном по объему шаре однородно. Найдите напряжен­ность этого поля, если расстояние от центра шара до центра полости /, а объемная плот­ность заряда шара р.

Решение. Искомую напряженность поля внутри полости проще всего найти с помощью принципа суперпозиции. Идея заключается в следующем. Если бы полости не было, поле Е[ в точке А (рис. 20) создавалось бы всем равномерно заряженным шаром. Такое поле нам известно (см. задачу 1). Но эту напряженность Е_: можно рассматри­вать как векторную сумму искомой напряженности Е поля, создаваемого ша­ром с полостью, и напряженности Щ поля, создаваемого меньшим шаром, по­сле удаления которого и образуется данная полость:

Е[ = Е + Щ. (5)

Теперь остается только подставить соответствующие выражения для Е[ и Щ.

(6)

Обозначим через Г[ вектор, проведенный в произвольную точку наблюде- ния А из центра О заряженного шара, а через г₂ — вектор, проведенный в точ- ку А из центра полости О'. Вектор 1 проведен из О в О'. Запишем формулу (2) задачи 1 в векторном виде: ^

Е,(г

где R — радиус шара. Подставляя сюда заряд q шара (без полости) q = -л:Я^лр, перепишем (6) следующим образом:

Ei^l) =*"з ^ЛР^Т1-

(7)

Очевидно, что точно такой же формулой выражается напряженность поля, создаваемого меньшим шаром, после удаления которого образуется полость:

лрт₂.

(8)

4 4

Е = к--яр(г, — г₂) = к~ яр1,

Выражая теперь Е из (5) как разность Е] — Щ, с помощью (7) и (8) находим

(9)

поскольку, как видно из рис. 20, для любой точки наблюдения А внутри поло­сти г, — г₂ = 1. Из (9) следует, что во всех точках внутри полости напряжен­ность поля Е одинакова. Это и значит, что поле в полости однородно. Напря­женность Е направлена параллельно линии ОО', соединяющей центр ша.ра с центром полости, от О к О' при р > 0 и от О' к О при р < 0. Модуль напря­женности поля в полости зависит только от плотности заряда р и расстояния / и не зависит от радиусов R шара и г полости.

Отметим, что в случае, когда центр полости совпадает с центром шара (/ = 0), формула (9) дает равное нулю значение Е: напряженность поля в любой

точке внутри равномерно заряженного шарового слоя равна нулю.

4. Электрическое поле диполя. Най­ти напряженность и потенциал электри­ческого поля, создаваемого диполем — двумя равными по модулю и разноимен­ными зарядами q и — q, находящимися на расстоянии / друг от друга, — в точке, отстоящей на расстояние г, большое по сравнению с размером диполя /.

Решение. Найти электрическое поле, создаваемое парой точечных заря­дов, не составляет большого труда. В со­ответствии с принципом суперпозиции напряженность такого поля равна век­торной сумме напряженностей полей, создаваемых каждым зарядом, а по­тенциал — алгебраической сумме потенциалов. Поэтому, обозначая через Г[ и г₂ расстояния от зарядов + q и — q до точки наблюдения А (рис. 21), имеем для потенциала

(10)

а выражения для модулей соответствующих напряженностей Е₊ и Е_ имеют вид

E₊ = k^r, E. = k4r; (11)

направления векторов Е₊ и Е_ и результирующего вектора Е показаны на рисунке.

Эти формулы справедливы для любых значений расстояний г₁ и г₂. Смысл задачи заключается в нахождении удобных для дальнейших применений вы­ражений, которые были бы справедливы на больших расстояниях от диполя.

д Электрическое действие заряженного тела на расстоянии, большом по сравнению с его размерами, определяется полным зарядом этого тела Q. Чем дальше от тела, тем меньше отлича­ется создаваемое им электрическое поле от поля точечного заря­да: это поле почти сферически-симметрично, его потенциал убы­вает с расстоянием как 1/г, а напряженность — как 1/г².

Если же тело в целом электрически нейтрально, т. е. его пол­ный заряд Q равен нулю, то это вовсе не означает, что оно со­всем не создает электрического поля.

В самом деле, электрически нейтральные молекулы вещества именно благодаря электростатическому взаимодействию между собой объединяются и образуют кристаллы или жидкости.

Для расчета электрического поля простейшей электрически нейтральной системы — диполя удобно несколько преобразовать выражения (10) и (11). Диполь принято характеризовать ди-польным моментом р, модуль |__Д/^<—*/cose которого равен произведению ql, а направление выбирается вдоль _{Рис 22 Вычисление потенциала ди}_ оси диполя от отрицательного _{поля в Т0Ч}ке А заряда к положительному

(рис.22). Далее удобно вместо г₁ и г₂ ввести расстояние г от середины диполя и угол 9 между вектором дипольного момента и направлением на точку наблюдения. Как видно из рис. 22, при 1/г«-1 разность расстояний г₁ — г₂ можно записать в виде

r_rr₂«lcose. (12)

В то же время произведение г/₂в знаменателе формулы (10) можно заменить на г². В результате формула (10) для потенци­ала принимает вид

, ql cos е , р cos 9 /, on

Ф = *—Г~ = ^к—Г^-■ (¹³)

г т

В отличие от потенциала поля точечного заряда, убывающего как 1/г, потенциал электрического поля диполя убывает с рас­стоянием быстрее — как 1/г². Разумеется, поле диполя обладает осевой, а не сферической, симметрией, поэтому его потенциал зависит не только от расстояния г, но и от направления на точку наблюдения, характеризуемого углом 9.

При получении формулы для напряженности удобно предста­вить результирующий вектор Е на рис. 21 не как сумму векторов Е₊ и Е_, а как сумму двух взаимно перпендикулярных состав­ляющих, одна из которых, Е_г, направлена вдоль радиуса-вектора г, характеризующего положение точки А относительно середины диполя, а другая, Е₉, перпендикулярна ей (рис. 23). На больших расстояниях от диполя, когда l/r«l, векторы Е₊ и Е_ направ­лены почти в противоположные стороны и мало отличаются по модулю. При приближенном нахождении Е_г нужно учитывать разницу векторов Е₊ и Е_ по модулю, но можно пренебречь тем, что они направлены не строго в противоположные стороны. На-

оборот, при вычислении Е₀ можно пренебречь различием векто­ров Е₊ и Е_ по модулю, но нужно обязательно учесть их некол­линеарность.

Записав с помощью формул (11) выражение для Е_г в виде Е_г~Е₊-Е.. = ка{\-\)=ка , (М)

можно при 1«г, как и при вычислении потенциала, заменить в знаменателе r_vr₂ на г², а в числителе — сумму г, + г₂ на 2г и разность r₂ — г₁ на / cos8. В результате из (14) получаем

£,«/fc^cos9. (15)

к Щ cos 9.

г

6:

При вычислении Е_в следует учесть, что угол между векто­рами Е₊ и Е отличается от л на малую величину 6, для ко­торой, как видно из рис. 23, справедливо

/ sin в

'«1.

Учитывая, что для Е_в можно приближенно написать Е_е « £+6, а в выражении для Е₊ заменить г₁ на г, окончательно получаем

Е_е « к sin 9.

(16)

Формулы (15) и (16) позволяют представить себе картину линий напряженности электрического поля диполя (рис. 24). В точках, лежащих на оси диполя, где угол 0 равен 0 или л, Е_в = 0 и, следовательно, напряженность поля направлена вдоль оси. Из формулы (15) видно, что направление совпадает с на­правлением дипольного момента р как при 0 = 0, так и при

Д9

»Д8

Рис. 25. Нахождение связи модуля перемещения As с изменением угла

0 = тс. Действительно, при 0 = л значение Е_г отрицательно. Это значит, что там вектор Е направлен к диполю (рис. 24). Во всех точках плоскости, перпендикулярной оси диполя и прохо­дящей через его середину, обращается в нуль радиальная со­ставляющая Е_г напряженности поля. Напряженность поля в этих точках перпендикулярна плоскости и направлена в сторо­ну, противоположную направлению дипольного момента р. Кар­тина силовых линий на рис. 24 симметрична относительно оси диполя.

Формулы (15) и (16) для напряженности поля диполя можно получить иначе, используя найденное ранее выражение (13) для потенциала. Для этого воспользуемся тем, что в соответствии с формулой (10) §4 проекция напряженности поля на любое на­правление E_s связана с изменением потенциала А«р при переме­щении вдоль этого направления на расстояние As соотношением

Чтобы найти Е_г, нужно совершить перемещение вдоль ради­ус-вектора, т. е. положить в (17) As равным Аг. В данном случае это сводится к дифференцированию выражения (13) для ф по г при фиксированном 9. В результате получаем формулу (15).

Совершенно аналогично, для нахождения Е_в нужно совер­шить перемещение As перпендикулярно радиусу-вектору г в на­правлении возрастания угла 6. При этом, как видно из рис. 25, перемещение As = гД9 и вычисление по формуле

с помощью выражения (13) для потенциала приводит к (16).

Формулы (15) и (16) важны потому, что они определяют электрическое поле на большом расстоянии не только для настоящего диполя, т. е. двух точечных разноименных заря­дов q и —q, но и для любой электрически нейтральной сис­темы зарядов, у которой центры распределения положитель­ных и отрицательных зарядов не совпадают. Другими слова­ми, на достаточно большом расстоянии любое тело с суммарным зарядом Q = 0 будет похоже не на точечный за­ряд, а на диполь. Для него можно подобрать диполь с мо­ментом р так, чтобы создаваемое диполем поле на большом расстоянии было практически эквивалентно полю такого тела со сложным распределением заряда. а

• Поясните на качественном уровне (без формул), почему сила, действу­ющая на пробный заряд внутри равномерно заряженного шара, пропор­циональна расстоянию до центра шара. Почему в центре шара эта сила равна нулю?

• Почему на графике напряженности поля равномерно заряженного шара есть излом при г = R, а на графике потенциала излома нет?

• Рассмотрите характер равновесия пробного заряда в задаче 2, если за­ряд q_x отрицательный, a q₂ — положительный, а также для случая, когда q_x и q₂ одного знака.

• При решении задачи 3 мы опирались на принцип суперпозиции, при­меняя его не к совокупности точечных зарядов, а к распределенным по объему зарядам. Приведите обоснование такой возможности.

• Почему для напряженности поля, создаваемого в точке А меньшим ша­ром, можно использовать ту же формулу (7), заменив в ней г_х на г₂?

• В каких случаях тело со сложным распределением заряда можно на большом расстоянии приближенно заменить точечным зарядом, а в ка­ких — диполем?

• По какому закону убывает с расстоянием напряженность поля и по­тенциал электрического поля диполя? Сравните с полем точечного за­ряда.

• Как по-вашему, может ли создавать какое-либо электрическое поле тело, у которого равны нулю и полный заряд, и дипольный момент?