§ 6.5. Параметрические взаимодействия

При параметрическом взаимодействии т мод с положительными частотами <Oj условие стационарности имеет вид закона сохранения энергии для яг-фотонного процесса:

т

Дю= 2 s,-to, = 0, (6.5.1)

') Напомним, что световые солитоны (с яплощадьк» 2it) образуются также в об­ласти резонансного поглощения за счет двухуровнев энгармонизма {§ 5.1).

где S(=±Ii й>£ = ш(й,-) > 0. Согласно одномерной модели в беско­нечном слое взаимодействуют лишь моды, удовлетворяющие закону сохранения поперечного импульса поля

ДА,-0

(6.5.2)

где UAf=2^sc*i'- Формально (1) и (2) следует из уравнений Макс- велла при трехмерном фурье-преобразовании (§ 6.3). В экспери- менте время т и сечение А = а* взаимодействия всегда ограничены, поэтому (1) и (2) выполняются лишь с точностью порядка Ifa

соответственно:

|Дш|^1/х, jAfej

Л (а.

(6.5.3)

В настоящем разделе мы, как правило, будем для простоты пренебрегать линейным поглощением (а₍ = 0). При этом взаимодей­ствие т мод в одномерном приближении согласно (6.3.24) описы­вается следующей системой уравнений:

di

d£* 2jisi<i)i

(6.5.4)

ICIli

где

(6.5.5)

£,- = Дб при Sf=l и El. при s = —1, x^im~^u—свертка тензора не­линейной восприимчивости с ортами поляризации, /г = и cos 9 cos р, л—показатель преломления, 0 и о — углы между вектором Пойн-тинга и осью г и вектором к соответственно, Д = Д£_г. Уравнения для E_t, Е_т имеют аналогичный вид и получаются перестанов­кой индексов.

Из (4) следует, что параметрическое взаимодействие эффективно лишь при достаточно малых |Д|, т.е. при сохранении продольного импульса поля:

(6.5.6)

Условие синхронизма Ak —• 0 резко сокращает число существен­ных «взаимодействий» —комбинаций величин \к_{, v_t, s_;), особенно в анизотропной среде, где показатель преломления n_v(co, &, ф) = = c&/ej_v (к) зависит не только от частоты, но и от индекса поляри­зации -v = 1, 2, и от направления ft = A/ie = J9, ф).

Приближение заданной накачки — ближняя зона. Пусть й_1г>0 и £₁(0)=0, т. е. мода с номером 1 не возбуждается внешним источником. При достаточно малых нелинейности, толщине слоя или падающих полях накачки Я_г(0) (1=2, . . . , т) можно пренебречь влиянием не­линейности на накачку, т. е. полагать в правой части (4) нелинейную поляризацию Р_г(г) с частотой Wi заданной функцией координат, опре-

деляемой пространственным распределением свободных падающих полей.

В случае заданной поляризации из (4), при учете определения (6.3.19), находим следующее выражение для амплитуды моды (ft, v), возбуждаемой в однородной прозрачной линейной среде фурье-компо-нентой поляризации:

£v(*)- fT*"* fdv_e-"'evPK, г), (6.5.7)

где и—групповая скорость. Заметим, что (7) определяет поле из­лучения вне V при любой форме излучающей области V.

В случае плоскопараллельного слоя с толщиной г из (4) следует

El (г) = _*ЕШ^ _{Е% {0)}.. ,_{Еш (0)} ^±, (6.5.8а)

с у

1М-(Щ-Г^-^и-^г' sin* (^/-(Ч-■ -'-(0),

16fii.. .и

(6.5.86)

где 7_ftj~cn_k\E_k\^z/'8ii=fi(d_kFk_S —■ продольная компонента плотности потока энергии Bfc-й моде и sinc(x)=(s[n х)1х. Формулы (8) определяют эффективность параметрического преобразования частоты света.

Заметим, что «новая» мода (ft,, определена через моды на-

качки Aj, . . . , к_т условиями (1), (2) лишь с точностью до типа поля- ризации V! и знака оч продольной составляющей (г,_г (см. (6.3.16)). Иначе говоря, каждая комбина- ция поляризованных волн накач- ки 2^si*i' . . - , возбуждает, в принципе, четыре волны с ча- стотой (»!, различающиеся индек- сами V! = l, 2 и Gi=±I- Однако обычно множитель sinc²(Az/2) в (86) сильно подавляет волну с А₁₂< <С0 — примерно в (к_1ггУ раз (рис. 6.13).

Итак, б приближении заданной накачки новые моды возбуждаются

пропорционально произведению интенсивностей падающих полей, квад­рату нелинейной восприимчивости и — при синхронизме (|Д|г<^1)— квадрату длины взаимодействия. При обратном неравенстве г^Е заме­няется на (A/2)~²sin^s(Az/2)~2M^E, т. е. при рассогласовании фазовых скоростей амплитуда новой моды периодически обращается в нуль. Расстояние л/|Д|, на котором интенсивность моды изменяется моно­тонно, называется длиной когерентности.

Дальняя зона. Практически формулы (8), как и вообще одномерное приближение с конечным числом поперечных мод, определяют поле Лишь в ближней зоне нелинейного образца, в которой дифракционные

IS1

эффекты за счет конечного сечения А области взаимодействия несуще­ственны. Однако в приближении заданной накачки нет необходимости использовать разложение по модам и одномерную модель, так как задача сводится к решению одного волнового уравнения (6.3.2) при заданном распределении монохроматических источников /'(со, г), т. е. к определению функции Грина G(co, г) уравнения Гельмгольца. Эта функция имеет особенно простой вид в случае однородной изотропной среды и большого расстояния г от источников до точки наблюдения.

Мы уже определили функцию Грина уравнений Максвелла в со, fc-представлении (см. (4.1.20)). Можно показать, что ее трехмерное фу рье-преобразование в первом порядке по ?/г, т. е. для волновой зоны, дает следующее выражение:

О («, г)«Ц-е<*'П(г), (6.5.9)

где n_afl = 6_HB—г_аг$—оператор проектирования на плоскость, пер­пендикулярную направлению r = r/r и k = /г (со) аз/с. Пусть r^>kA (дальняя зона), тогда (9) приводит к следующей связи между полем и сторонней поляризацией (ср. (7)):

■(со, r) = ~e^,krJdV'e-'*"'n(r)-P(w, г'),

(6.5.10)

где k = kr и г соединяет какую-либо точку внутри области V, содержащей источники, и точку наблюдения. Таким образом, при больших V поле излучения в дальней зоне пропорционально фурье-образу сторонней поляризации.

Рассмотрим генерацию поля с частотой to_t, заданной накачкой, состоящей из т~ 1 плоских волн. Нелинейная поляризация при V —*■ со также является плоской волной с частотой и волновым век­тором, равными

т т

а>₁= — 2 s^-. К — - 2 ^s,*i- (6.5.11)

Пусть тензор %""~^L) отличен от нуля в параллелепипеде с разме­рами а, Ь, с, тогда из (10) следует [при s_x = I)

е* (со,, г)=$ег** ₍п ■ -с"""¹¹ • £_а. - £ J V/ (г), (6.5.12)

f (г) =\&г'е'Д^ь'-^г'/У= sine (Ak_xa{2) sine (№_yb/2)sine (Ak_tcf2), (6.5.13)

ДЛнЛдЗУ/с—К. (6.5,14)

Диаграмма направленности поля и>_г при заданном К опреде­ляется в основном функцией f(r). Для эффективного преобразова­ния частоты длина вектора К должна быть близка к n^)Jc*=k_x, при этом излучение максимально в направлении К (для которого f ж\) и имеет заметную величину в телесном угле порядка i\lA,

где Л — площадь проекции излучающего объема на перпендикуляр­ную К плоскость (рис. 6.14).

Взаимодействие грех волн. Рассмотрим в рамках одномерной модели взаимодействие трех волн или мод с частотами а₁-^[-щг=а}₉ за счет квадратичной нелинейности, которая имеет заметную вели­чину лишь в пьезокристаллах. Для выполнения условия синхронизма Дй== А_а—#1 = 0 в области прозрачности кристалл должен быть двупреломляющим и иметь определенную ориентацию осей относи­тельно падающих лучей (рис. 6.15).

о

Перенормируем амплитуды волн так, чтобы их квадраты рав­нялись Fi—плотности продольного потока энергии в единицах Ещ (см, (6.3,29)). Из (4) (или (6.3.31)) при s_t = s₂ = — % 1 следует (полагаем, что все волны попутные, гс,- > 0):

йа,1йг = 1^а1а₃, (6.5.15)

dOzfdz = фе^'а^Ог, (6.5.16)

йа,1йг=-фе~**а_ха„ (6.5.17)

где

ps(32n^aA«₁o)_I£e_i/<7^,n₁n₁n_s)^,'« х, '(6.5.18)

Д = &k_t, гх^(2> («₃ = щ + «О: e,e_tet> (6.5.19)

Здесь свертку % можно считать вещественной величиной, инва­риантной к одновременной перестановке частот и ортов поляриза­ции е_} (§ 6.1),

Умножая эти уравнения на а\, убеждаемся, что скорости изме­нения потоков dFjIdz в модах 1 и 2 равны, а в модах 1 и 3 имеют обратные знаки. Таким образом, поток энергии 2 A(o_fF_t- лнщь"пе-рераспределяется (без поглощения) между тремя модами, причем доля каждой моды пропорциональна ее частоте (соотношения

^{Мэнли—Роу—см. § 6.3):}

(6.5.20)

где

AF^FtM-FtW).

(6.5.21)

Имеется еще третий независимый интеграл (6.3.49) уравнений (15) — (17), определяющий разность фаз. Эти интегралы позволяют свести решение уравнений (15) — (17) к одной квадратуре. В результате за­висимость аДг) выражается через эллиптические функции, описываю­щие периодический обмен энергией между тремя модами [34]. Мы здесь рассмотрим крайние случаи, когда интенсивность одной из волн много больше интенсивности двух других (приближение заданной накачки, или параметрическое приближение).

Преобразование частоты вверх. Пусть F_lj^>F_il F_s (низкочастотная заданная накачка), a_ia=al₀ и Д=0, тогда из (16), (17) следует

dajdz=iya_s, (6.5.22)

dajdz = iya_s, (6.5.23)

у — ра₁₀= [У2&а_%щ1с*п^п₂п₃] (6.5.24)

Эти уравнения легко решаются подстановкой a^cfi^: а, ■- а_ы cos yz + ia_sll sin yz, a_s = a₃₀ cos yz + ia_M sin yz.

(6.5.25)

Таким образом, моды 2 и 3, аналогично связанным маятникам, периодически (на длине я/2у) обмениваются энергией (в единицах Й*>,-) в соответствии с (20) (рис. 6.16).

_{* -* . *}

XXX

. а

Рнс. 6.16. Параметрическое взаимодействие в случае низкочастотной заданной на­качки: ii) зависимость интенсивности от расстояния 2, 6} два варианта спектра излу­чения (стрелки указывают направление передачи энергии)

Оценим характерную длину параметрического взаимодействия 2л^=1/т>яг Vi/4n^sx£i₀. Пусть Я₂ = Х₃— 1 мкм, п_г=\, %=10~^вГс-¹, /₁₀= 100МВт/см^г, тогда г_лч = 0,3см.

При ц_эо = 0 из (25) следует

Л-Л.зтЧг/г^),

F_t = F_t

cos³ (г/г

N1.)

(6.5.26)

Эта формула описывает параметрическое сложение частоты, или пре­образование частоты вверх (up-conversion), которое используется, в частности, для визуализации ИК-излучения. Выходная интенсив­ность преобразователя при длине взаимодействия z=n,z_Nl/2 достигает максимума, равного (в фотонах) входной интенсивности. При этом эффективность преобразования в обычных единицах равна ш_а/ю₂;>1.

Легко обобщить (26) на случай Д^О. При этом эффект сложения час­тоты описывается формулой

F_s - F_ia [у sin (T'z)/T']\ Г = + A*/4)i/». (6.5.27)

Отсюда при Д²^>4у² снова получаем (86). Сравнение (26), (27) с (8) показывает, что приближение двух заданных накачек a_ll2 = const применимо лишь при (2т>/Д)² <^ I. При этом период пространствен­ных биений определяется волновой расстройкой Д, а не интенсив­ностью накачки у.

Параметрическое усиление и генерация. Пусть F_3u^>F_u F^ (вы­сокочастотная накачка), тогда вместо (22) — (24) имеем

dajdz = iyal, dajdz^iya'^ (6.5.28)

Эта система имеет решение (ср. (25))

а_х = a_la ch у г + ш_г*₀ sh yz, а₂ = а₂₀ ch у z -f- la"_ia sh yz.

Если a₁₀ = 0, то (ср. (26))

(6.5.29)

	yz	= (G-l)Fau,
F2 = F20ch3	yz	= GFiU,

(6.5.30)

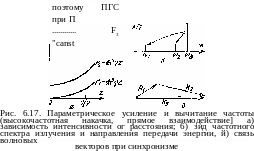
где G — коэффициент параметрического усиления. Эти формулы опи­сывают эффекты вычитания частоты ы₃—to₂—^-coj и параметрического усиления. В отличие от случая низкочастотной накачки интенсивнос­ти здесь нарастают неограниченно по экспоненциальному закону (рис. 6.17). Отметим, что (30) удовлетворяет соотношениям Мэнли — Роу (20): ДЛ=Д^_Я=(<5—1) F_l0.

Нетрудно показать, что в случае Д=£0 эффекты усиления и вычита­ния частоты при высокочастотной накачке описываются формулой <Ч>. (27))

G = 1 -f [у sh(Гг)/Г]=, Г = (у²- Д²/4)' ².

(6.5.31)

Заметим, что при у²<Д^Е/4 экспоненциальный рост сменяется биениями.

При наличии положительной обратной связи на частоте »i и/или ю₂ (рис. 6.18) усилитель превращается в параметрический генератор света (ПГС). Одна из частот при этом (например, a>i) называется сигнальной, а другая (оь) — холостой. Конечно, для возникновения автоколеба­

ломления п.

ний параметрическое усиление должно компенсировать не учитываемое здесь поглощение и потери в зеркалах Частоты генерации ПГС опре­деляются в основном условием синхронизма, т. е. показателями пре-

фиксированной частоте накачки со_а

можно плавно перестраивать изменением ориентации или температуры кристалла. Существующие ПГС с импульсной лазерной накачкой перекрывают диапазон Х^0,4—20 мкм, удачно дополняя перестраивае­мые лазеры на красителях. Оптимизируя параметры кристалла, сфокусированного пучка накачки и резонатора, удается полу­чить генерацию даже в непрерывном ре­жиме.

Встречное взаимодействие. Пусть волны накачки и сигнала распространяются в слое «направо» (#,₂, к_Яг > 0), а холостая волна— «налево» {k_iz < 0). Условие синхронизма при этом удается осу­ществить за счет сильного двупреломления или аномальной диспер­сии. Для встречной волны &_г > я/2 и л_а<0¹), так что вместо (28) имеем

dajdz = iyal, dajdz = — iya\

(6.5.32)

имеет толщину /, тогда граничные условия имеют s (I) = а_ы. Легко проверить, что решениями (32)

Пусть слой вид o₁(0) = a₁₀,

(6.5.33)

являются следующие функции (рис. 6.19).

й,= [a_lQ cos [у (I—г)]-\-iali sin-ysj/cosy/, а_г = {a_2f cos т>г + (flio sin [у (I—z)]}/cosy/,

полагаем у вещественным числом. При yl-^-n/2 эти решения устремля­ются к бесконечности, т. е. возникают автоколебания, несмотря на

Точнее, знак п=п cos 9 cos р определяется углом 0=O:£p между лучевым век­тором и осью г, однако угол анизотропии в полосе прозрачности не превышает не­скольких градусов, и мы им здесь пренебрегаем.

отсутствие зеркал. Можно считать, что при встречном взаимодействии имеет место распределенная обратная связь (аналогичный эффект имеет место в лампе обратной волны).

100

0,5 z }

Рис. 6 19. Параметрическое усиление и вычитание частоты в случае встречного вза-вмодейетвяя- а) зависимость интенсивности (в единицах F_M) от координаты г (в единицах Vy) при F_2I=0 и 7?= 1,5; коэффициент усиления равен l/cos^s(l,5)^200: б) треугольник синхронизма при встречном взаимодействии

Генерация второй гармоники (ГВГ) в одномерном приближении и при отсутствии линейного поглощения описывается уравнениями (16), (17) при замене индексов 3 —^ 2 —*-1:

dajdz = JpV ⁱ ■ й,Ч. (6.5.34а)

da₃ldz = ip>-^a\l2, (6.5.346)

где

В = (64л*М/с³ггЯ)^ш X. ⁴ = Kt—^kw (6.5.35)

г=У*^1^:2'(—«i; 2_Wl, — todie&e^tywi— 2w,; co_L, <u_t) ; e_Ee,e,.

(6.5.36)

Коэффициент 2 в последнем выражении добавлен в соответствии со связью (6.1.13).

Легко проверить, что эти уравнения удовлетворяют условию со­хранения энергии поля, которое совпадает здесь с соотношением Мэн-лн — Роу:

10,14-210,1*=^, (6.5.37)

Коэффициент 2 связан с тем, что каждый фотон гармоники имеет вдвое большую энергию, чем фотон накачки. Второй интеграл уравнений (34) имеет согласно (6.3.49) вид

[ а, |* [4 -261а_г | cos (ф,-2(р₁ + Дг)] - С„

(6.5 38)

где ф_£ — фазы комплексных амплитуд в,.

Решения уравнений (34) в общем случае описывают периодический (в пространстве) обмен энергией между модами накачки и гармоники (эти решения выражаются через эллиптический синус [34, 41]).

Мы здесь ограничимся наиболее простым и важным случаем, когда Д=0, a_j(0)=0. При этом, полагая в (3 8) г=0, находим С₂=0 и, следо­вательно, при любых z имеем cos(p = 0. где ф=ф_г—2qv Таким обра­зом, сдвиг фаз между модами не меняется. Легко показать, что и сами

фазы неизменны. Для этого подставим в (346) а,=Ь,ехр((ф,)(Ь^0): dbjdz - (112) Щ sin ф = {1 /2) | В | Ы, (6 5 39)

d%/dz = (p*j/2&,) cos ф = 0. (6.5.40)

Из второго уравнения следует, что ф, и ф₉ не зависят от г, а из перво­го — что направление передачи энергии (из первой гармоники во вто­рую или наоборот) зависит от знаков <р и р. в рассматриваемом случае Ъ_г нарастает (от нуля), поэтому р sin <р>0, т. е. <р=(я/2) sign %. Подставив (37) при С, = Ь% в (39), легко находим решение:

V 2Ь_г

Отсюда

|Р1

аЪ^г = Щ{Ь\,-2Щ)!2, db₂ f 2

Arth

fi_a = (l/K2)&₁₀triY3, b^bjchyz,

(6.5.41) (6.5 42)

(6.5 43)

где

(6.5 44)

7^IP|oio/K2=2(2₃i/c«₁)^s/a «,1x1

тенсивности накачки 1

Итак, при синхронизме интенсивность второй гармоники /_гг(г) монотонно нарастает как th^!yz, достигая при уг^>1 исходной ин-

/_1г(0) (рис. 6 20) Интенсивность накачки при этом падает до нуля как 1/сп^ауг при неизменной фазе. При г = 1/у эффективность гвг т| равна 58% по энергии и 29% по числу фо­тонов При Д^о или а₂(0)ФО монотонные решения сменяются периодическими и т| падает.

В 1 z 2

Рис 6 20 Генерация второй гармони­ки по горизонтали — расстояние (в единицах \1у). по вертикали — потоки фотонов накачки и гармоники (в еди­ницах f_lfl) При г^>1 каждые два фо­тона накачки превращаются в один фотон с удвоенной частотой

Практически с помощью мощ­ных импульсных лазеров удается получить 1] в несколько десятков процентов. Отметим, что синхрон­ная гвг в пьезокристаллах имеет важное прикладное значение, поз­воляя сдвигать частоту лазеров вверх на целую октаву. Упомянем также гораздо более слабые эффекты, не требующие син­хронизма,-— ГВГ при отражении от нецентросимметричной среды [34] и некогерентное рассеяние света с частотой 2о> нецентросимметрич-ными молекулами [35], а также — при учете «магнитного» ангармо­низма — любыми молекулами, атомами и свободными электронами (§ 6.2).

Заметим, что принятое выше условие £₂(+0)=0 не совсем точьи соответствует обычному эксперименту, в котором равно нулю падаю­щее снаружи поле гармоники, а прошедшее и отраженные поля £₂(+0), Ег{—0) отличны от нуля из-за требования непрерывности тангенциаль­ных составляющих полей Е_г, Н₂ на границе [34], Однако практически £^(±0) весьма малы.

Матрица рассеяния. Параметрическое взаимодействие двух мод в нелинейном слое в приближении заданной накачки приводит к ли­нейной связи между входными и выходными амплитудами, которую б общем случае можно записать в виде

«i = ffiitfiO + £ia^am. ^ = £₂i«h, + £_s<l<4. (6 5.45)

Коэффициенты g_h образуют двумерную матрицу рассеяния данного образца, зависящую от длины слоя поглощения а,, нелинейности %, амплитуды накачки а₃с, волновой расстройки Д и т. д, При учете от­ражений от границ слоя она становится четырехмерной, а при учете дифракции (г. е. конечных поперечных размеров Л) — бесконечномер­ной.

Матрица рассеяния должна обладать определенной симметрией, следующей из общих принципов, в частности из соотношений Мэнли — Роу (20). Обмен фотонами между модами в случае, когда падающие поля a_L и а₂ статистически независимы, описывается энергетической матри­цей рассеяния G_ry=lg_(/I²:

fi=O_uF,-+0_ltF„₍ F,=G_aF_ie+Q»F_M. (6.5.46)

Подстановка (46) в (20)*дает

(di—1) J^c'jo+G₁₂r⁷so=(Gf_J—1) Fsa+Gsi-Fio-

Но F, и Fa можно варьировать независимо, следовательно, матрица рассеяния прозрачного слоя должна удовлетворять связям

<?u-l=Ga, G„-I=G„. (6-5.47)

Система (28) симметрична по индексам 1, 2, поэтому Сц=0.._гз^С и имеется только один независимый элемент энергетической матрицы рассеяния — коэффициент передачи G. В результате (46) принимает вид

f,=GF_l0+(G-l)f_ie, F.=GF_tv+(G—\) F_lb. (6.5.48)

^DПараметрическое рассеяние света*

Согласно квантовой теории в принци­пе возможен трехфотонный переход, при котором прозрачное вещество — атом или кристалл — поглощает фо­тон из моды fe₃ и излучает пару фото­нов в моды k_t и k₂, возвращаясь в ис­ходное состояние (рис. 6.21). Вероят­ность такого перехода пропорциональ­на (JV.+ l) (ЛГ₂ + 1) JV», где ЛГ,—началь­ные числа фотонов в модах и единицы Появляются из-за квантовых флуктуа­ции амплитуд люд в основном состоя­нии (гл. 7). Вероятность обратного процесса — с поглощением фотонов в модах Ai, k₂ и излучением в моде А_э— пропорциональна A^jVsfjVi-f-l). В итоге скорость рождения пар фотонов будет пропорциональна

№

разности

N₁ = If, = - N₃ ~ {N₁ + ЛГ, + I) - ВД. (6.5.49 a)

Отсюда в первом порядке по iV₃ следует

ЛГ_Х—N_lc=Nz—N_i0~N_IO+N_2ll+1. (6.5.496)

Таким образом, вещество под действием излучения с частотой со₃ генерирует пары фотонов с частотами ^ и <в_а=со₃—o)_lt лежащими в широком диапазоне — от нуля до частоты падающего излучения. В случае макроскопического вещества частоты и направления излуче­ния связаны условием синхронизма к₃=к±-\-кц. Это явление наблю­дается в двупреломляющих пьезокристаллах и называется параметри­ческим рассеянием (ПР) или параметрической люминесценцией [5, 37, 58]. ПР можно трактовать как проявление квантовых шумов парамет­рического усилителя света.

Коэффициент пропорциональности в (496) должен соответствовать коэффициенту преобразования G_i2=Q—I, найденному выше в (31) в рамках классической нелинейной оптики. Следовательно (ср. (48)),

JVi=AT„+(&-l)(JV_lo+Ar_fo+l)-OJV₁,+(0-l)(Ar_l,+ I). (6.5.50)

Аналогичное выражение для получается перестановкой индексов 1_Я 2. Здесь величина О—1 уже необязательно линейна по интенсивности накачки.

Полученное выражение позволяет сформулировать следующее пра­вило. Для учета спонтанного излучения при классическом описании параметрического усилителя следует во входные холостые ^г) моды до­бавлять по одному лишнему фотону. Тот же результат согласно (50) получается при более общем преобразовании

Nu-+Nu+p, N„->N_m+q. tfi-WVi+p,

где p+q=\, O^p^l. В частности, можно ко всем числам фотонов на моду добавлять по полфотона.

Квантовые шумы согласно (50) дают по О—1 фотона в каждой вы­ходной моде параметрического усилителя, где О — коэффициент уси­ления для этой моды. Аналогичный результат (закон Кирхгофа) имеет место для квантового и рамановского усилителей (см. (7.1.7) и (6.4.18)).

Заметим, что из (49а) при N^=N,=0 следует, что при трехчастот-ном преобразовании частоты вверх (низкочастотная накачка) кванто­вые флуктуации отсутствуют. В случае четырех частотного взаимодей­ствия возможен распад двух фотонов накачки на пару фотонов с часто­тами <!> и 2<1>_я—из, лежащими в интервале 0—2а (гиперпараметрическое рассеяние или рассеяние света на свете).

Перейдем от чисел фотонов на моду к спектральной яркости. С помощью (50) и (6.4 20) находим при Л7_1в = 0 (полагаем pj. = 0)

^l) «Холостой» модой по отношению к рассматриваемой к сигнальной в моде с ча­стотой <i)j называется мода с частотой ь>з=щ—wi-

/«o(*i) = W«o<*i) = (*«>i/23i4) [G (fei) -1 ], (6.5.51)

где F_aQ= dFld<& dQ — поток фотонов в направлении к_г с частотой <»v (^i)' приходящийся на единицу телесного угла, площади (перпен­дикулярной ft_x) и круговой частоты. Величина /_ыа(А. г) называется спектральной яркостью (иногда —просто интенсивностью) некоге­рентного излучения. Напомним, что яркость не меняется в направ­лении распространения (в случае прозрачной среды).

Итак, интенсивность шумов идеального усилителя, деленная на G—1 (т. е. отнесенная ко входу),

(6.5.52)

Эту величину естественно называть интенсивностью нулевых флук­туации макрополя (с одним типом поляризации) или «спектральной яркостью вакуума», она соответствует присутствию в каждой моде по одному фотону. Интенсивность флуктуации на единичный интервал длин волн при ?t=l мкм и /1 = 1

На = ] daldX | IJS hc*№ да 0,6 Вт/(А■ см²■ ср). (6.5.53)

Таким образом, связь между интенсивностью и числом фотонов на моду имеет вид

(6 5.54)

Оценим также яркостную (эффективную) температуру сверхлю­минесценции на выходе идеального усилителя. Из формулы Планка (2.5.5) и закона Кирхгофа JV = G — 1 следует

Г_э4, (А) = &ю/к In (I + -Vjf *) = — W In (1 — G*¹) ж

«(£a>/_K)G~10^eK, (6.5.55)

Последняя оценка сделана для к = 1 мкм и G=100.

Подставив (31) и (52) в (51), получим следующее выражение для интенсивности квантовых шумов параметрического усилителя:

La (k) = sh* Д»(А)/4)1"/]/<1 ~4*(fe)/4_Y³), (6.5 56)

где /—толщина нелинейного слоя, Д (ft) —отклонение от синхро- низма для моды k и 7 ~ (^см- (28)). Согласно (56) интенсив- ность ПР имеет резкий максимум на частотах и направлениях {а, 9, ф}, удовлетворяющих условию синхронизма Дй~0.

Это условие определяет частотно-угловой спектр ПР ш (■&), где ■& — угол рассеяния, т. е. угол между наблюдаемым волновым вектором ft и вектором накачки k_s. Зависимость частоты от угла ф, как правило, Можно не учитывать, т. е. спектр ПР обладает осевой симметрией от­носительно направления ft₉. Поле с данной частотой а излучается вдоль Конуса под определенным углом &(&>). Как видно из рис. 6.22, частот­ный спектр ПР при накачке в синей области спектра перекрывает ши­рокую область в ИК и видимом диапазонах. Видимое излучение на-

т

правлено преимущественно вперед, под углами, не превышающими нескольких градусов, что связано с небольшой величиной двупрелом-ления кристаллов в области прозрачности.

При приближении холостой частоты к собственным частотам ре­шетки кристалла, которые лежат обычно в области сотен обратных сантиметров, ПР непрерывно переходит в комбинационное рассеяние на полярнтонах и оптических фононах. При этом % резонансно возрас­тает за счет вклада электронно-ядерного ангармонизма (§ 6.2), но одно­временно растет и линейное поглощение на холостой частоте сс₂, так

Рис. 6.22. Частотно-угловой спектр параметрического рассеяния в ниобате лития при различных длинах волн накачки А₃- §\ — угол конуса, вдоль которого излучается волна Я,. Угол % между лучом накачки и осью кристалла равен 90". Приуменьше­нии 6_э разрыв в спектре (для Я.₃<0,53 мкм) исчезает

что интегральная по частоте яркость /_я меняется мало. Конечно, при малых холостых частотах и aj^>\ (56) следует умножить на в1Ц*(<»₂/Г)+ -f-1, где Т — температура решетки и ^ — функция Планка.

ПР, как и рассеяние на полярнтонах, можно определить как рас­сеяние света накачки на флуктуациях поля в холостых модах, т. е. как рассеяние света на свете, аналогично тому, как рассеяние Мандель­штама — Бриллюэна является рассеянием света на звуке.

Существенными особенностями явления ПР, отличающими его от других видов рассеяния света в веществе, является, во-первых, широкий непрерывный спектр, не связанный непосредственно с собственными частотами вещества, и, во-вторых, двухфотонный характер излуче­ния — при слабой накачке (т-/<^?1) сигнальные и холостые фотоны излу­чаются только парами, практически одновременно.

Отметим, что кроме когерентного (направленного вперед) излуче­ния возможно некогерентное ПР на отдельных нецентросимметричных молекулах (точнее, на флуктуациях плотности и ориентации таких молекул). При этом условие синхронизма не играет существенной роли, так как дефицит импульса поля забирает молекула.

Пусть у/<^1 и пяй 1, тогда из (56) находим интенсивность спон­танного ПР (СПР) в направлении ft и с частотой ю(й):

1ш(ft) = iVayW sine* [A (ft) 1/2] =

= 4Ас-⁵ш*ш_Х^Е;^а/_ао sine⁵ [Д (ft) 1/2], (6.5,57)

где (o=w_s—со и подразумеваются фиксированные индексы поляриза­ции, для которых Д минимально. Обратим внимание, что интенсивность СПР в направлениях точного синхронизма зависит от толщины нели­нейного слоя квадратично, что характерно для СПР. Пусть /_эо= = 1 Вт/см² и /=1 см, тогда усиление в направлении синхронизма имеет порядок £?=14-1>^гР~1-Ы0"⁷ (см. оценку после (25)) и из (55) приА = =0,5 мкм следует Т_Эф~1800 К- Такое излучение легко наблюдается невооруженным глазом и имеет вид цветных колец. Заметим, что фак­тический коэффициент передачи образца G' при такой накачке всегда меньше единицы из-за потерь на отражение, поглощение и рассеяние.

Эффективная частотная ширина спектра СПР Аы при фиксиро­ванном направлении наблюдения определяется, как и полоса парамет­рического усиления, шириной синхронизма, т. е. условием Д/=±п. Если ограничиться линейным разложением функции Д(»), то

Д» = (2л//)|аД/5й)|-¹да2л/|т₁—т₃|, (6.5.58)

где Т; = 1/к₍. Согласно последней формуле, справедливой при кол-линеарном синхронизме и а>₁Ф&^, ширина спектра СПР (в герцах) равна обратному времени запаздывания [в секундах) сигнального фо­тона относительно холостого при пересечении области взаимодей­ствия. Обычно Д(о/2лс ти, 10см^-1 при / = 1 см.

При yl^>l (56) описывает параметрическую сверхлюминесценцию, или вынужденное параметрическое рассеяние (ВПР). Согласно при­веденным оценкам ВПР наблюдается при импульсной накачке с ин­тенсивностью порядка (ООМВт/см² и выше. Конечно, ВПР практи­чески имеет место (как и параметрическая генерация) лишь в продольном направлении (Ь ~ 0) на частотах коллинеарного синхро­низма оэ_;(0). Дело в том, что, как следует из геометрии, эффектив­ная длина взаимодействия /_аф в случае узкого пучка накачки (йД-^I) резко сокращается (как a/sin 0) при т>^>й/'. Общую мощ­ность излучения ВПР можно представить в виде

$> = /иаДиДАЛ™ I⁴Jie^Au,AQA/4, (6.5.59)

где мы ввели эффективные полосу частот, телесный угол н сечение (ср. оценку для ВКР (6.4.22)). ВПР используется, как и параметри­ческая генерация, для регулируемого сдвига частоты лазерного из­лучения.

"Рассеяние света на поляритонах описывается системой (15) — (17) при добавлении в одно из уравнений линейного поглощения. В при­ближении заданной высокочастотной накачки взаимодействие стоксо-вой (сигнальной) и папяритонной (холостой) волн определяется урав­нениями

daJdz—iyaW*², (6.5.60а)

dajdz ± 6а_г = ± iya{e'^, (6.5.606)

где b=aJ2, y~$a_w (см. (28)) и нижние знаки соответствуют встречной холостой волне. В поляритонной области спектра, т. е. вблизи соб­ственных частот решетки, холостая волна сильно поглощается, так