§6.2. Модели оптического энгармонизма

В зависимости от особенностей вещества, его состояния, частот дей­ству ющих полей и других условий эксперимента основной вклад в на­блюдаемые нелинейные эффекты могут давать различные механизмы.

^г) Термин «точечный» связан с тем, что при вращениях одна точка (начало коор­динат) неподвижна — в отличие от трансляционных преобразований координат.

Ниже будут рассмотрены несколько частных классических "моделей" оптического энгармонизма, а затем будет дана общая квантовая схема расчета нелинейных восприимчивостей.

Ангармонизм свободного электрона. Пусть на электрон (или на любую заряженную частицу) действует плоская монохроматическая волна Е с линейной поляризацией вдоль оси х и направлением распро­странения вдоль оси z. При учете магнитной части силы Лоренца не­релятивистские уравнения движения электрона имеют вид (е<.0)

_{X + 2уХ = ± ( Ех-12Н W J- (1 - 1 Z)Е.}

^{Y ™ \ * < «; «л * j} ₍₆^._2Л⁾

Z+2yZ = — XE, ' ' тс

где у—феноменологическая константа затухания, которая обеспе­чивает установление стационарной амплитуды после включения периодического поля, и

E^E_X(Z, t)*teE_xex.p[ikZ{t)—iuit\ = H_y{Z, t) (6.2.2)

— поле в точке нахождения частицы. Затухание может вызываться столкновениями, а также реакцией излучения — потерями на излуче­ние (радиационное трение). Предположим, что продольное смещение электрона Z мало, тогда в (2) можно полагать Z—0 (днпольное прибли­жение, т. е. приближение нулевого порядка по kZ).

Будем искать установившееся решение (1) в виде ряда Фурье ме­тодом последовательных приближений по амплитуде поля:

R = Я^ш + R™ + ... = Re (R,e-^ш+R₂e~^Ш1 +...), (6.2.3)

где R = {X, У, Z). В первом приближении можно пренебречь дейст­вием магнитного поля, так что отклик электрона линеен:

Отсюда тензор линейной поляризуемости электрона, связывающий амплитуды дипольного момента d, = eR₁ и поля Е_х, равен

°^И = - ,т{а+Щ ^в«Р* <⁶'²"⁵>

В нашей модели нейтрализующий положительный заряд отсутствует н мы определяем дипольный момент относительно начала координат R=0. Умножив ее на плотность электронов jV, найдем линейную восприимчивость %^ш холодной (эффект Доплера мал) плазмы (ср. (4.2.13)).

Итак, при <в^>у линейная поляризуемость электрона

(6.2.6)

где г_е =е*1тс* & 3-10~" см—классический радиус электрона. Заме­тим, что г_е связан с другими характерными масштабами с размер­ностью дайны через постоянную тонкой структуры e³/fic* ж 1/137:

К/2 = 137а₀ = 137^_е = 137»/-,,

(6.2.7)

где "л_в= 2лК s^l/R р£ 10 ⁵ см—длина волны, соответствующая потен­циалу ионизации атома водорода 13,6 эВ (R = metpiafac—постоян­ная Ридберга), a₀=^v™^s^5-10'^s — боровский радиус и X_c=h/mcm я5 4-10"¹¹ см —комптоновская длина волны. Пусть Я = Я„, тогда

— а—4а|я*6.10-" см^а (6.2.8)

— поляризуемость свободного электрона в УФ-диапазоне имеет порядок объема атома водорода, т. е. порядок поляризуемости связанного электрона в отсутствие резонанса.

Чтобы найти второе приближение, следует вместо R в левые части (1) подставить R^l2\ а в правые—При этом сила Лоренца имеет компоненты с нулевой и двойной частотой:

Ff = [etc) X^WE = (1 /2) k Ima(| E, 1* + £»«-*""). (6.2.9)

Под действием силы с двойной частотой возникают продольные колебания электрона с частотой 2ш. Амплитуда этих колебаний согласно (1) и (9) равна

Ып&т (ce-f-ty) ((o-|-i2y)

_4р.

/72

(6.2.10)

В последнем равенстве мы ввели тензор квадратичной поляризуемости свободной частицы р\ связывающий амплитуды поля и дипольного момента eZf^} на двойной частоте. Итак, квадратичная поляризуемость свободного электрона при а>^>у имеет порядок

| (51 х е³/т²са³ — (еК/тс") a ss a/E^Z⁶.

(6.2.11)

Здесь E_NL—характерный параметр, равный амплитуде поля, при которой линейный и квадратичный отклики одинаковы: Z^la, = X"^ul. При Хг=\

Ejfl? — elr.K**\W Гс,

(6.2.12)

что соответствует интенсивности 10⁴⁰ Вт/см^3,). Ниже будет показано, что в случае связанного электрона даже в отсутствие резонанса эн­гармонизм на два порядка больше:

ЯЖ^э«⁵~су137со,

где

10' Гс.

(6.2.13)

') В гауссовой системе единиц Е и Н имеют одинаковые размерности, и поэтому £~можно измерять в гауссах ( 1 Гс=300 Б/см).

Умножив р на плотность электронов, получаем квадратичную вос­приимчивость плазмы:

| _хи> | = #Ntm*<x>* - | х¹" \/Effl?. (6.2.14)

Итак, один из фундаментальных источников ангармонизма вещест­ва — сила Лоренца. Отметим наличие в знаменателе (14) скорости света, что характерно для магнитных эф­фектов.

to

Согласно (И) отношение Z^'i'X'¹¹ имеет порядок EjE_NL, в то время как kZ^y% ~ ~(EJE_N,y. Следовательно, при £_Д<^£_Л7 использование дипольного приближения для расчета р* оправдано.

Если не учитывать статической силы светового давления, то согласно (4) и (10) электрон под действием монохроматическо­го поля описывает в плоскости хг «вось­мерку» (рис. 6.2). Вынужденные колебания электрона вдоль поля X^{V{t) сопровожда­ются дипольным излучением во все сторо­ны (кроме точного направления оси х) — это пгомсоноеское или, при учете отдачи, комп-тоноескоерассеяние. В то же время продоль­ные колебания электрона Z^IS (() дают дипольное излучение на частоте второй гармоники падающего поля, т. е. эффект удвоения частоты света. Максимум излучения второй гармоники происходит в попереч­ной плоскости ху, а излучение вдоль направления распространения первичного поля отсутствует. Такая структура тензора квадратичной поляризуемости свободного электрона препятствует когерентному сло­жению амплитуд поля второй гармоники в случае макроскопического образца — плазмы или полупроводника.

Итак, электроны в плазме, металле или полупроводнике дают, кроме томсоновского, еще некогерентное рассеяние с двойной частотой и интенсивностью, пропорциональной $²N. Связанные электроны в ато­мах и молекулах также обладают квадратичной поляризуемостью, ко­торая приводит к некогерентному рассеянию на двойной частоте, на­зываемому гиперрэлеевским. С квантовой точки зрения оно объясняется элементарным процессом поглощения двух фотонов падающего света и излучением фотона с двойной энергией (рис. 6.1, о). При равенстве фазовых скоростей падающей волны и ее второй гармоники (н(со) = = п(2а) — так называемое условие пространственного синхронизма) и при подходящей структуре тензора х^(а| кроме слабого, почти изо­тропного гиперрэлеевского излучения имеется гораздо более интен­сивное продольное излучение, пропорциональное p²jV^s=x^(2E (§6.5).

"Давление света. Постоянная составляющая силы Лоренца (9) определяет статическую силу F_Q светового давления, действующего на электрон со стороны бегущей волны. Согласно (9) F₀ пропорциональ­на мнимой части линейной поляризуемости электрона а", т. е. рас­сеиваемой им мощности ^^,^аа"|£₁1^э/2 (см. 4.1.12)) или сечению

■

⁵ д. н. Клышко ¹²⁹ взаимодействия

(6.2.15)

где /== с| £j |⁸/вя— интенсивность плоской волны. Поэтому силу дав­ления света можно представить в виде

(6 2.1b)

Под действием этой силы электрон будет ускоряться, однако в плазме столкновения приводят к установлению постоянной дрей­фовой скорости Z₀= Fjmy, где у=]/т и х—время между столкно­вениями (напомним, что у—скорость затухания колебательного движения, которая может превышав у). Возникающий вдоль луча света постоянный ток, пропорциональный \Е^[^г, можно рассматри­вать как эффект отического выпрямления (в диэлектриках эффектом выпрямления или dc-эффектом называют появление статического поля Е„~\Е₁\¹).

Пусть (л^>у, тогда согласно (5) a"=2ye^s/ma\ Оценим F_t в слу­чае, когда единственная причина затухания колебаний электрона — потери на излучение (радиационное трение). Согласно (I) сила тре­ния в первом порядке равна — 2утХ^а]. Умножая ее на скорость X¹¹¹ и усредняя по периоду, находим мощность потерь'. 5* —уты* [Л⁴!¹!². Приравнивая это выражение мощности дипольного излуче­ния (5.2.3), получаем

2у,ш = а"/а' = 2г_е/ЗК. (6.2.17)

Этот же результат следует т (5.2.8) в случае единичной силы ос­циллятора (4 2.23). Теперь (16) принимает вид

£i|73.

(6.2.18)

Сравнивая (16) и (18), находил! томсоновское сечение для рассеяния на свободном электроне:

о^вя^/Э. (6.2.19)

С фотонной точки зрения давление света возникает в результате передачи электрону импульса поглощаемых фотонов и симметричного томсоновского (или комптоновского) их переизлучения во все стороны. Подчеркнем, что мы рассмотрели лишь среднее значение силы, которая испытывает квантовые флуктуации [431.

Мы нашли силу светового давления на свободный электрон в случае бегущей волны. Аналогичный анализ можно провести и для более сложной пространственной конфигурации светового поля (отклонение электрона в поле стоячей волны называют эффектом Капицы — Ди­рака). Существенно, что в неоднородном поле средняя по периоду сила Лоренца возникает и при а"=0. В этрм случае F_a определяется

рлного большей величиной а' и можно полагать а"=0, Эта сила связана _с обменом между различными плоскими волнами и называется вынуж­денной (в отличие от спонтанной силы (16)).

Смещение электрона AR(t) под действием монохроматического поля равно a,E(R₀, t)ie, где а =— те^г/а£—поляризуемость и R₀— невозмущенная координата электрона. Отсюда находим среднюю силу Лоренца:

F„=-aEy.H!c = k Ima£_ex/£/2 (6.2.20)

(последнее выражение применимо и при комплексной поляризуемо­сти). Заметим, что в плоской бегущей волне ЁН ~ sin Ы costof —* О и чю в общем случае сила F_a не пропорциональна среднему вектору Пойнтинга S₀ = cReE_a xH'JSk.

Рассмотрим случай двух плоских волн:

2

2 £„ехр(1Й_п-Я₀-Ич\).

Н_я = к_пу,Е,_с, А„ = А>/с

При <х" = 0 в (20) остаются лишь «перекрестные» компоненты:

F, = (112) ak Im (£tх Hi — E\ x ff_±) e¹* =

= (1 2)a\m{-Ak{E_i-E;)-tEAEi-ki)-El(E_l-K)\e^lt\ (6.2.21)

где -ф = Д* #₀ + Ф, ДА^*! — k₂, ф^ф!—(р₄.

Легко убедиться, что часть /v пропорциональную ДА, можно представить в «градиентном» виде с эффективным потенциалом —<хЕ*/2 (происхождение множителя 1/2 ясно из (4.1.25));

£_ж = аУ|£_ар/4. (6.2.22)

Заметим, что эта часть F_a, называемая силой Миллера, исчезает согласно (21) при ортогональных поляризациях волн. В случае встреч­ных волн (ft_s= — ftj) с одинаковой линейной поляризацией F₀ = F_M:

^F₀ ^{= — aki Е,Е}₂ ^{sin (2k,-R, + ф). (6.2.23)}

Под действием этой силы заряженные частицы стремятся сгруппиро­ваться в узлах стоячей волны.

В общем случае поле состоит из непрерывного множества плоских волн и силу светового давления можно найти интегрированием (21) По ki и к₂ (при эгом градиентная часть (22) сохраняет свой вид). Отме­тим, что при учете отдачи электрона частоты взаимодействующих волн различны. Соответствующее явление называется вынужденным эффек­том Комптона.

Рассмотрим далее силу давления свега на связанные в атоме или молекуле электроны, т. е. на нейтральные поляризующиеся частицы. Будем исходить из эффективного потенциала вида = — d-E(r),

5*

13!

где d—индуцированный дипольный момент и г —координата центра масс частицы. Отсюда (см. (4.1.36))

(6.2.24)

или F_a = d$dE$ldx_a- Полагая здесь

£, = (1/2)£>^£(*^г-^м()+к. с. d_t = cc(ci>)£^,+, + K. с.

и выделяя постоянную составляющую, получаем снова (16).

Рассмотрим сперва резонансное давление. П^сть затухание опять обусловлено лишь собственным излучением частицы, т. е. резонанс­ной люминесценцией (§ 5.2), тогда резонанс имеет минимальную (естественную) ширину 2у_ра1= А. При этом согласно (2 3 9) а=2л?Ч^а и из (15), (16) следует а" = Х°'!2 и

= &

(6.2.25)

Таким образом, резонансное давление света на связанный электрон е Ъ?{т%— 137^е раз больше, чем на свободный (при радиационном зату­хании) Это различие определяется отношением сечений резонансного и томсоновского рассеяний.

Оценка (25) относится к случаю, когда заселен только нижний уровень, вообще же

а'«* (1/2) K^s А = k*A™,2 (1 + 2WJ,), (6.2.26)

где А и Д¹°>— относительные разности населенностей с учетом насы- щения и без него (§ 4.3), It⁷, — вероятность перехода и Т, — время продольной релаксации. При радиационной релаксации 1/Д,

Согласно (26) при инверсии населенностей сила давления направлена навстречу лучу света, что на фотонном языке объясняется отдачей фотонов, излучаемых при вынужденных переходах вперед.

При сильном насыщении поглощаемая атомом мощность со­гласно (4.3.22) равна hfftA^w/2T_lt так что из (16) следует

F_a = fikA^I2T_t

(6.2.27)

■— сила пропорциональна импульсу падающих фотонов и числу рассеи­ваемых за единицу времени фотонов. Пусть )ь = 1 мкм и ^4=10⁶ с^-1, тогда F₀=3- Ю^-17 дин и при m=3- 1СГ" г ускорение достигает 10^е см/с" (интенсивность насыщающего света при этом много больше 10~⁴ Вт/см^г).

Резонансное давление лазерного света предоставляет необычные возможности: с его помощью можно ускорять, отклонять, фокусиро­вать пучки нейтральных молекул, разделять изотопы, «пленять» моле­кулы в ограниченной области пространства, уменьшать их тепловые скорости [431.

Стрикционный энгармонизм. Пусть теперь все частоты поля лежат в области прозрачности вещества, тогда можно пренебречь дисперсией и полагать поляризуемость частиц вещественной константой. При этом сила принимает вид

F = a\£>J2 = aVB ^{h 1} • Е< ->. (6.2.28)

Здесь черта означает усреднение по высокочастотным компонентам — ведь нас интересует статическая или медленно, по сравнению с часто­тами поля и молекулы, меняющаяся часть силы, которая действует на молекулу в целом (обозначения Е¹-' см. в § 7.2). Градиентной силе (28) соответствует эффективный потенциал моле­кулы ^ = — «£'/2-

Плотность дополнительной энергии вещества и плотность силы в оптическом поле б; дут в N раз больше (см. (4.1.32)):

d = — ypi 2 = — (п* — 1) Ё~'!8п, (6.2.29а)

1 = уУ&/2, (6.2.296)

где % = waN, А'—плотность молекул, которая предполагается однородной, и n=V б -— показатель преломления.

Мы здесь пренебрегли взаимодействием молекул, что допустимо лишь в случае достаточно малой N. Можно показать, что в общем случае (см. [22], с. 361) следует в (296) сделать замену

⁽⁶-²³⁰⁾

где р — плотность вещества. Например, из формулы Клаузнса—Мо-зотти, которую легко получить из (4.2.9):

следует

dp \ /оЧп(Л 3

дв,'т~\ дг ,'г ^—(в —1)<8-2)'

так что в случае плотной среды (296) надо умножить на поправку Лоренца (е-\-2)/3.

В бегущей плоской волне \Е^! не имеет постоянной составляющей, поэтому F = 0 (мы рассматриваем сейчас область, где а" = 0 и свя­занная с диссипацией спонтанная сила (16) исчезает). Однако в стоя­чей плоской волне Е = 2Е_У cos (кг) cos (out), и из (28) следует (ср (23)):

£_г = — akElsm(2kz). (6.2 32)

Таким образом, при о>0 частицы будут собираться в пучностях волны. Силу (32), пропорциональную поляризуемости, называют вы­нужденной.

В ограниченных пучках света существует статический поперечный градиент квадрата поля и частицы при &О-0 стремятся к оси пучка.

В стационарных условиях плотность силы (296) должна компенсиро­ваться повышением давления Др и плотности частиц &.М в центральной части пучка:

±NfN = Ap'p=*$_T Др,

(6.2.33)

(6.2.34)

где р_г—изотермическая сжимаемость вещества. Эти формулы описы­вают эффект электрошрикции в световом поле.

Приращение плотности частиц в л>че света вызовет изменение восприимчивости вещества

Д_Х = а ДЛ' = р_г-/,²1Е, |-/4. (6.2.35)

С другой стороны, по определению

Р? = t^s> («■ = »-»4 «) I Е_г \* Е, = \_XE_U

так что мы получаем для вклада элект. рострикции в кубическую восприимчивость выражение

_у1»=р_1ХШ1,4. (б 2.38)

Отсюда находим характерный нелинейный параметр

£|^x'^,,/x^,J, = ^₇x'¹¹-

(6 2.37)

В жидкостях n«l,5 (x«fO,l) is $_TxlQ~^w см-7дин (напомним, что (5 як 1/pii², где и —скорость зв^ка), так чю х^и) Ю^-" см',эрг, E_VL & at 10⁶ Гс.

Градиентная сила (28) и соответствующее давление (33) имеют большое прикладное значение: они позволяют генерировать мощные ультразвуковые волны с помощью бигармонических лазерных полей. Этой же силой объясняется эффект вынужденного рассеяния Мандель­штама — Бриллюэна (см. ниже). Стрикционная нелинейность (36) является одной из причин самофокусировки света (другой важный ме­ханизм — оптический эффект Керра, т. е. ориентация анизотропных молекул в жидкостях в луче света с линейной поляризацией — см. ниже).

Ангармонический осциллятор, В классической теории дисперсии Лоренца (§ 4.2) электроны в атомах полагают гармоническими осцил­ляторами. Естественно рассмотреть оптическую нелинейность вещества с помощью модели ангармонического осциллятора. Пусть частица на­ходится в потенциале

У³ (х) = то>1х'-/<2— тг\х* '3 —еЕх, (6.2.38)

где е — заряд частицы и ц — малый параметр, определяющий откло­нение формы потенциальной ямы от параболической (для простоты берем одномерную модель). Из (38) находим уравнение движения:

Dxssx + 2yx + tolx^eE/m + r\x¹. (6 2 39)

Пусть внешнее поле £ — бигармоническое. Будем искать стацио­нарное решение в виде ряда теории возмущений:

^{х(0 = 2 *я1 (О- х'"" ~ 4й"1 Ет' (6.2.40)}

где т=1, 2, 4, 8, . . Подставив (40) в (39) и приравняв слагаемые одного порядка малости, получим решение с помощью итераций:

Dx^w = eE'm, i^"' \ (6.2.41)

В первом порядке

х_п = а К) E,Je, а (со) = eimD (со), ^VD^^4ZJ

где

D (со) = ь>1 — (й² — *2yw = D* (— со).

Во втором порядке согласно (41) возникают компоненты x[t) с частотами 0, 2а_L, 2«_а, ю₁ ± о>₂. Рассмотрим отклик д"_э на частоте Ms^Wj + Oj. Из (41) при т=1 следует

^₃=1^л1>(й1₃)=р (ш₃=ы₂ + <и,) EgEt'e,

где

Р (ш₃ = щ + (о_г) = х\е^!/тЮ («,) Z?(<в₂) £ (»,).

(6.2.43)

При W! = ±(o_; р содержит дополнительный множитель 1/2 (см. (6.1.13)). В соответствии с (6.1.14), (6.1.15) поляризуемость р" инвариантна к пе­рестановке местами двух последних аргументов, а также к одновре­менному изменению знака всех трех частот и мнимой единицы. Однако согласно (43) переставлять первый аргумент со вторым или третьим можно лишь при отсутствии резонанса на переставляемых частотах, когда ]со„—tool^Y (ср. (6.1.20)). Переход от поляризуемости одного осциллятора р к восприимчивости среды %^<s> осуществляется умноже­нием на плотность частиц JV.

Итак, модель ангармонического осциллятора предсказывает резкое увеличение квадратичной поляризуемости 6 (в Q=b->j2y раз) вблизи резонансов — когда один из трех ее аргументов приближается к соб­ственной частоте соо. При этом р¹ становится комплексной величиной. Из сравнения (43) и (42) следует, что 6 пропорциональна произведению линейных поляризуемостей на соответствующих частотах:

P(a>_J=(o_a+(»₁)~"r|a((i)₃) a(w_s) a (mi). (6.2.44)

Отметим, что квадратичные восприимчивости многих диэлектриче­ских кристаллов в области прозрачности (между собственными часто­тами решетки н электронов) удовлетворяют соотношению

-/»~n(o),)nK)n(cu,) (6.2.45)

с одной и той же константой пропорциональности для разных кри­сталлов (эмпирическое правило Миллера).

Наша модель не учитывает отличия действующего (локального) поля £_лок от макроскопического, усредненного по атомным неодно-родностям поля £. Согласно Лоренцу в кубическом кристалле Е_Л1>К1Е —(е4-2)!3 (эту поправку нужно вводить лишь в случае ди­электриков, а в металлах или полупроводниках £,„„ = £). Поляри­зация среды Р, вызываемая заданной сторонней поляризацией Р_сп также в (s-(-2)/3 раз превышает Р_сг В результате квадратичная восприимчивость y}^i!, определяемая по отношению к макроскопиче­ским величинам, равна

где rim, определена для локальных величин. В некубических кри­сталлах поправка имеет тензорный характер. Формулы (44)—(46) указывают на тесную связь линейных и нелинейных свойств среды.

Пусть при смещении а^- = й_с линейная еЕ_а= тч>1а₀ и нелинейная г\пш% силы в (39) сравниваются, тогда v\ — al/a₀ (здесь ^—характер­ное поле, удерживающее заряд около положения равновесия). Отсюда при у, «_;1<^о)₀ следует оценка

£_ж~оуВ ~ moJ/Tje ~ пш%а_й'г = Е_й. (6.2.47)

Таким образом, отношение квадратичной поляризации к линейной имеет порядок £,/£₀ (ср. (12)). Для атома водорода под а_е следует понимать радиус Бора Р/те², а под ш₀ —граничную частоту иони­зации e²i2ha_b. При этом £₀ = е/2ао я» 10⁷ Гс.

Кубический потенциал (38) приводит согласно (41) к появлению лишь четных гармоник 2<о, 4ю, 8со... Для образования нечетных гармо­ник потенциал должен иметь слагаемое порядка х⁴. Отметим, что по­тенциал (38) даже при £=0 не центросимметричен: он изменяет знак при инверсии координаты х—v —х. Полезно рассмотреть трехмерную модель с помощью потенциала (331:

(г) = ти>1 _ах_ах_а/2 — т)_ттх_ах^. (6.2.48)

Романовский ангармонизм. Спонтанный эффект Романа, или спон­танное комбинационное рассеяние (СКР), был обнаружен Мандель­штамом и Ландсбергом и, независимо от них, Раманом в 1928 г.— за­долго до создания лазеров. Соответствующий вынужденный эффект (ВКР) впервые наблюдался лишь в 1962 г.

При СКР падающий на вещество монохроматический свет (накачка) поляризует молекулы с оптической частотой <x>_t. В результате они при­обретают дипольный момент

d(i)=a₁£_Icos etj, (6.2.49)

для простоты линейную поляризуемость молекулы at,,=a(<iy,) полагаем вещественной скалярной величиной. Излучение молекулярных дипо­лей (49) дает рэлеевское рассеяние.

Учтем теперь внутримолекулярные колебания ядер с собственной частотой Q_a<^.o)i, которые возбуждаются в результате столкновений.

Колебания ядер около положений равновесия Q(f) медленно модули­руют окружающее их электронное «облако». При этом модулируются н'все электронные параметры молекулы, включая ее оптическую поля­ризуемость: a(t) = (da.'dQ) Q(t). Эта картина основана на так называе­мом адиабатическом приближении, использующем сильное превышение собственных частот электронов а_и над Q₀ (обычно о>а<'2яс~ 10⁵ см^-1, Й₀.''2лс^10⁵ см^-1). При учете колебаний ядер (49) принимает вид моду­лированного по амплитуде колебания

d(t)=(a₁+-jftQtCQsQ,t}E₁cosa_it, (6.2.50)

где Q$—амплитуда колебаний ядер.

В результате рассеянное диполями излучение содержит кроме «несущем (рэлеевской) компоненты ь»! еще две боковые составляю­щие — стоксову a_±~Q_a и антистоксову (Ох-гОо. В случае многоатом­ной молекулы рамановский спектр содержит нормальные частоты мо­лекулы (некоторые колебания из-за симметрии не влияют на а). При учете анизотропии а и вращения молекул индуцированный дилольный момент d(t) будет промодулирован также и с характерными вращатель­ными частотами молекулы.

Рассмотренная модуляционная картина основана на единственном нелинейном параметре daidQ, введенном Плачеком, и наглядно описы­вает спонтанный эффект (термин «спонтанный» относится здесь к ком­понентам поля с частотами g>,±Q|), которые отсутствуют в падающем поле и возникают «спонтанно»).

Чтобы описать вынужденные нелинейные эффекты, обусловленные параметрической связью ядер и электронов, полезно рассмотреть мо­дель двух связанных осцилляторов, определяемую потенциалом

У³ {х, Q) - mwlx²I2 + ,MQ£Q³/2 — щ'-Q—eEx. (6.2.51)

Здесь х и ш_п — координата и собственная частота электрона, Q и Я,— то же для колебаний ядер, г\—параметр связи, пропорциональный drx/dQ. Из (51) следует

х+2ух + ф = еЕ!т + 2r\Qxfm, (6.2.52а)

Q + 2r(5+QJQ= т\хЧМ. (6.2.526)

Эту модель для описания ВКР предложили Платоненко и Хохлов в 1964 г. Согласно (526) на ядра действует сила, пропорциональная квадрату смещения электрона, поэтому ядра будут сильно раскачи­ваться в случае, когда разность двух частот поля близка к Q_B. Пусть падающее поле — бигармоническое, причем <в,—ш_а^С~-£3₀. В линейном по полю приближении Q^(ll = 0 и

x%> = eEjmD_B, D_n^ to*—e% — i2ya>_a, п=1, 2. (6.2.53)

Оставим в силе трк² лишь резонансные слагаемые с частотой Q, про­порциональные х'^х^"*, тогда амплитуда вынужденных молекулярных колебаний с частотой U будет равна

Uq = т—з ¹ г = г- £,£,. [0.2 54)

2гИ(ао— Я*—(2Гй) 2Д>010₂

Итак, оптическое бигармоническое поле с подходящей разностью частот ^раскачивает» через посредство электронной оболочки внутри­молекулярные колебания ядер. Эти когерентные с падающим светом ко­лебания добавляются к равновесным тепловым колебаниям и вызывают дополнительное когерентное рассеяние на антистоксовой частоте w_s = ==ujj+fi=2u) i—<й₈ и на второй стоксовой частоте со₄г~ш_г—£2~2(о₂—о^. Кроме того, появляется кубическая поляризация на исходных часто­тах поля, вызывающая усиление поля с меньшей частотой £₂ и ослаб­ление поля с большей частотой E_t, Эффект романовского усиления и лежит в основе вынужденного комбинационного рассеяния.

Подставив (53) и (54) в (52), найдем

I P I* £ E\E^ V(S)		»lV/2Mm*
х1 —		D„Dj d2d;
х2 —
х3 —-		iyV/2Mmi
	mD-t	DaD$DiDs

(6.2.55)

Умножив x™ на eN, найдем кубическую поляризацию. Как пра­вило, в эксперименте частоты поля ь>„ (л=1, 2, 3) много меньше частот электронных переходов <о₀, поэтому В_Пъщ* {нерезонансное КР). В этом приближении из (55) следует

_Х<³¹ (а₁ <о₂) =- х^и> К = «_Е — (о,)* = x^w (щ = 2а»!- &>,) =

= С/[Й£—(и, — — (2Г(«, — а₂)], (6.2.56)

где C^xfe'N/Mm^l

Эти нелинейные восприимчивости описывают соответственно рома­новское поглощение (так как %^<П) (ш_х)" > 0 при ч>, > ы₂), романовское усиление («_г)" < 0) и когерентное антистоксово рассеяние (КАРС) с интенсивностью, пропорциональной | %^а) (й>_э) |^гКроме того, из (56) следует, что монохроматическая волна с изменяемой частотой о> при наличии второй волны с фиксированной частотой ю_г испытывает в области линейной прозрачности резонансную дисперсию в двух областях d>_L ± Й„ (рис. 6.3). Ширина этих резонансов 2Г определяется скоростью затухания молекулярных колебаний, причем в стоксовой области рамановская (или индуцированная) дисперсия имеет аномаль­ный характер.

Найдем связь нелинейных параметров т| и daldQ. Подставим Q = = Q₀cosQ₀2 в уравнение (52а). В первом порядке по п, из него сле­дует x₃ = r\e EyQjm^D^D^ Сравнение с (50) дает

= — ж — л. (6.2 57}

С помощью двухосцилляторной модели можно описывать и СКР. Для этого правую часть (526) следует заменить на стохастическую ланжевенову силу f(t), вызывающую равновесные тепловые (и кванто­вые) флуктуации Q(t). Эта сила б-коррелнрована, причем ее спектраль­ную плотность можно найти, приравнивая энергию флуктуации Q

_t

Рис. 6.3. Комби наиионная (рамановская) восприимчивость. Под действием накачки с частотой ч>1 восприимчивость вещества приобретает дополнительные резонансы на частотах О_с (Q_c — собственные частоты молекул). Существенно, что стоксов

резонанс обладает отрицательными потерями (внизу слева) и аномальной дисперсией показателя преломления (вверху слева)

равновесной энергии осциллятора. Другой метод описания СКР ис- пользует рамановский аналог ФДТ (§7.7), согласно которому флук- туации поляризации вещества на частоте ю определяются мнимой частью кубической восприимчивости [7. 371:

<Р* («) />')> =

= (ft/л) 8 (со—w') сАГ (— Q) х'*' (« = со—о), + щ)" | B_L \\ (6.2.58)

где

(Q) = [exp (ЙЯ/хГ)—l]-¹ - — Л(— Й)— 1, П = ю_ь—«. (6.2.59)

Здесь при £2 < 0 (антистоксова область) имеет смысл равно­весного числа фононов вУ*», а при Й > 0 (стоксова область) = = —(<jf_u+l)- Единица в последнем выражении соответствует кван­товым флуктуациям ядерной координаты Q, вызывающим стоксово рассеяние даже при Т=0 (антистоксово рассеяние при этом отсут­ствует). Элементарный процесс, соответствующий стоксову рассеянию, является двухфотонным. Он включает уничтожение фотона накачки и рождение стоксова фотона и фонона (рис. 6.1, ж).

Конечно, рассмотренная двух осциллятор на я модель, как и модель ангармонического осциллятора, имеет чисто качественный характер. Количественный расчет восприимчивости (даже линейной) весьма сложен и требует знания волновых функций и собственных частот системы (см. ниже).

Неупругое рассеяние света может быть связано также с возбуж­дением других степеней свободы вещества, например электронных.

При этом частота света изменяется на частоту какого-либо электрон­ного перехода атома или молекулы: й,-«_!=©_мэ^_и-^„)/А, Если падающее поле содержит две частоты такие, что »i-biB₂=w_m„>0 и молекула находится на нижнем уровне и, то может произойти одно­временное поглощение двух фотонов. При обратном процессе возбуж­денная молекула излучает два фотона (спонтанно или вынужденно).

В макроскопическом веществе свет взаимодействует не только с ло­кальными внутренними колебаниями частиц, но и с коллективными возбуждениями вещества, например с акустическими, температурными, спиновыми, плазменными волнами, с колебаниями ориентации молекул.

Равновесная хаотическая часть этих волн модулирует показатель преломления (ср. (35)), и в спектре рассеянного света появляются со­ответствующие боковые компоненты (о^ыцЬЙ. Наглядно рассеяние можно представлять как результат дифракции падающего света на бегущей решетке, образованной волнами давления, температуры и т. д. С квантовой точки зрения происходит рассеяние фотона падаю­щего света (накачки) /го^ с рождением или уничтожением кванта воз­буждения вещества Mi (фонона, магнона, плазмона, экситона, полярн-тона и т. д.). Для рассеяния на распространяющихся возбуждениях характерна зависимость частоты модуляции от направления наблюде­ния, т. е. от угла рассеяния: fi=Q (Щ. Эта зависимость является след­ствием условия Брегга при дифракции или, иначе, условия синхро­низма (закона сохранения импульса) k_x—А₂±<7=0 и закона дисперсии рассеивающей волны q=q(Q), где q — волновой вектор возбуждения вещества. Формально влияние синхронизма на рамановский энгармо­низм можно учесть, полагая, что кубичная восприимчивость зависит не только от частот, но и от волновых векторов (пространственная дисперсия).

Для описания вынужденного рассеяния на акустических волнах (РМБ ■—■ рассеяние Мандельштама ■— Бриллюта) и других коллек­тивных возбуждениях надо учесть неравновесную когерентную часть этих возбуждений, вызываемую бигармонической накачкой. Механизм возбуждения звука светом ясен из (33) — из-за электрострикцнн в веществе возникает источник переменного давления с разностной частотой Q:

Др(г, 0= (1/2)х^(,,[2(£_п/2)ехр(-<0 + к.

=■ (1/8) %^к"Е_гЕ\ exp (- ffli) + ... (6.2.60)

с. с.

Этот источник порождает волны плотности Др, распространяю­щиеся со скоростью звука v. Если волны накачки плоские, то Др —* — exp [i{k₁—ft_;) - г] и вынужденная звуковая волна будет иметь максимальную интенсивность при \ ft, — k_g \ = q = Q<v. Это условие синхронизма «выбирает» из непрерывного спектра акустических воз­буждений, занимающего область от нуля примерно до 10" Гц, одну (или две, при учете различия v для продольных и поперечных волн

б аморфном твердом теле) дискретную компоненту с частотой

Q = v | jfe, — k, [ ж 2vk sin (fi/2)

(6.2.61)

и шириной, определяемой коэффициентом поглощения звука.

"Температурный энгармонизм. Из (61) следует, что при 9^0 рас­сеяние на акустических волнах, т. е. на волнах давления Ар и плот­ности Др является неупругим: И~ифй (точнее, максимум рассеяния происходит при Й^О). Согласно (61) рассеяние с максимумом при <i^=0 может вызываться лишь ^распространяющимися возбуждения­ми, для которых и=0 или которые достаточно быстро затухают. Такое рассеяние происходит на флуктуациях температуры Д7" (или энтропни AS~AT), а также на флуктуациях концентрации АС в смесях и раст­ворах. Величины х^р, Т, С, ... (или р, S, ...) являются термодинами­ческими параметрами, задающими макроскопическое состояние вещест­ва, и их колебания — тепловые («спонтанные») или вынужденные (ко­герентные) — приводят к нарушению оптической однородности среды An —(дп'дх) Ах и к рассеянию света — спонтанному или вынужден­ному. Все эти рассеяния происходят с небольшим смещением частоты (по сравнению с рассеянием на молекулярных колебаниях) и объеди­няются под общим названием рэлеевское или молекулярное рассеяние 1361 (последний термин подчеркивает отличие от рассеяния на макро-неоднородностях—-пылинках и других включениях).

Интегральная по спектру интенсивность спонтанного рассеяния на параметре х пропорциональна среднему квадрату Ах², и ее можно рассчитывать термодинамически, однако форма спектра рассеянного света определяется кинетическими уравнениями, описывающими эво­люцию поля x(r, t). Например, при х=Т таким уравнением является уравнение диффузии

t—aVT^PlCjfi, (6.2.62)

в котором а — температуропроводности, 5^s — мощность сторонних источников теплоты на единицу объема, с_р— удельная теплоем­кость при постоянном давлении (вообще, надо одновременно с AT учитывать колебания давления Др при нагреве, но мы для простоты пренебрежем связью волн температуры и давления).

Решение (62) при 5>—0, которое описывает спонтанное темпера­турное рассеяние, можно представить как сумму плоских волн, экспо­ненциально затухающих во времени:

AT{r, ()»2V''-^V', (6.2.63)

где y^aq*. Как и в случае рассеяния на акустических волнах, рассеяние света с волновым вектором k, в направлении Й₂ обуслов­лено «температурной решеткой» с q— + (k,— Ь_г), однако согласно (63) эта решетка неподвижна, и поэтому дифракция на ней приводит к появлению в спектре рассеянного света упругой (несмещенной) линии с шириной

Аш = 2v = &ak^! sin³ (Ь,'2) (6.2.64)

(в жидкостях Лео ~ 10^й с^-1 при 0 = 90°). Обратная полуширина линии температурного (энтропийного) рассеяния х_т = ]/у = К^г/а имеет смысл времени диффузии температуры на расстояние длины волны =s|ft, — fe^l""¹. т. е. времени релаксации температурной решетки.

Механизм вынужденного температурного рассеяния (ВТР) и соот­ветствующего энгармонизма очевиден при наличии некоторого погло­щения (ВТР-2). Действительно, в случае бигармонического поля вынуждающая сила в (62) имеет переменную составляющую:

У (г, 0 = сох" Е-(г, 1) = <ах" Re E_rE, & <»-' (6.2.65)

которая порождает волну температуры

^{aT — ReTa^W'-0". (6.2.66)}

Ее амплитуда определяется подстановкой (65), (66) в (62):

Га = (6-2-67)

здесь ю fn о), ж о\^> | Й| и %" = %"(а).

Бегущая когерентная волна температуры (66) модулирует воспри­имчивость х (⁸ основном за счет падения плотности при тепловом расширении)¹):

поэтому волна восприимчивости имеет амплитуду

«■=££(#),*■«■

В результате возникает кубическая поляризация с частотами

Я«' (t) = A%(t)E(t) = Re ЫЕ₃е~^' + £",e"°>' + Е&-Ы + Е1е^ш>¹)?2.

(6.2.70)

Пусть £„ f₂ параллельны оси я, тогда из определения кубичес­кой восприимчивости находим

Отметим интересную особенность ВТР-2: здесь усиливаются антисток-совы компоненты (ср. (56)), т. е. в процессе распространения энергия поля перекачивается из низкочастотных компонент в высокочастотные (так как (ду1дТ)_р<.Щ.

^J) В идеальном газе N = p]x.T, поэтому хи-ар/иТ", и если пренебречь зави­симостью и от Т, то (д%!дТ)_р = — х/Т.

Для оценки температурного ангармонизма положим

w)r-$* ^е*~Т*"- П"-^- ^г. (6.2.72)

где т_£ = п/ас— время релаксации ноля. Тогда при [о, — ю_Е|т7<^1

£^^-^«-5^, (6-2.73)

где U ~3kTN{2—плотность внутренней энергии. Таким образом, «ели тг = т_£ (что при т£ = 10"⁸ с соответствует к = 0,003см^-1), то нелинейная поляризация сравнивается с линейной, когда энергия поля п*Е\(&к сравнивается с тепловой энергией вещества. Заметим, что если перейти от температуропроводности а к теплопроводности Х~арс_р, то E%_L можно представить в виде 8пХц^гГх£.

Электрокалорнческкй энгармонизм. Температурный ангармонизм имеет место и в совершенно прозрачном веществе за счет оптического электрокалорического эффекта (соответствующее вынужденное рассея­ние называется ВТР-1).

Рассмотрим простейшую модель, описывающую влияние электри­ческого поля на температуру непоглощающего вещества. При включе­нии поля (постоянного или переменного) уровни энергии молекул за счет эффекта Штарка смещаются, и их населенности перестают соот­ветствовать температуре термостата, роль которого обычно играют поступательные и вращательные степени свободы молекул (или коле­бания кристаллической решетки). За время релаксации 7\ происходит перераспределение населенностей с соответствующим изменением энергии термостата '), н в результате его температура изменяется. Отметим, что аналогичный магнитокалорический эффект применяется для получения сверхнизких температур (метод адиабатического раз­магничивания). Более точное объяснение следует из определения тем­пературы для замкнутой системы (микроканонического ансамбля):

\/T=dSfdU=K д(\п g)tdU, (6.2.74)

где S — энтропия, U — внутренняя энергия и g{U) — плотность энергетических состояний. Последняя зависит от расположения уров­ней и поэтому изменяется при включении поля.

Оценим вклад электрокалорического эффекта в температурный ан­гармонизм. Согласно (4.1.32) при поляризации диэлектрика его термо­динамические потенциалы получают приращение v=—y}E₁\ⁱ'4 (на единицу объема). Выберем в качестве независимых переменных Тир, тогда энтропия определяется через производную потенциала Гиббса Ф (Т, р) по температуре, поэтому изменение 5 при поляризации равно

■) Здесь учитывается конечная теплоемкость внешних степеней свободы.

Умножив AS па. Т, получим приращение тепла AQ, а умножив на —Т/с_рр, найдем приращение температуры:

4с _рр \дТ }_р\

Из сравнения с (62) следует, что роль поглощаемой мощности в случае прозрачного вещества играет величина

^J»**- at 4lS7J_fT' (0.-2.77)

Б случае бигармонического ноля получаем

^_в»(г, П = —~{^г)шЕ₁-Е^^^г~(6.2.78)

Сравнивая (78) с (65), находим отношение электрокалор; веского энгармонизма к энгармонизму (71), связанному с поглощением;

Отсюда следует, что коэффициент поглощения, эквивалентный электро­калорическому эффекту, не велик:

InSiT

СП

~ 10-*см~\ (6.2.80)

где принято Q=I0»c-\ 7" = 30ОК, (д%{дТ)_р= — \й~* К."¹.

Заметим, наконец, что за счет связи волн плотности и температуры электрострикция также дает вклад в температурный энгармонизм (см. (141, с. 249).

Ориентационный энгармонизм. Как уже отмечалось, вращение анизотропных молекул в газе также модулирует рассеянный свет, что при учете квантования вращательного движения приводит к появле­нию дискретных боковых компонент у рэлеевской (несмещенной) и ра-мановской линий в спектре спонтанного рассеяния. Однако при боль­шой плотности частиц молекула не успевает сделать полного оборота за время ориентационной релаксации т, поэтому в жидкостях линии вращательного спектра перекрываются и рэлеевская линия приобре­тает широкий «пьедестал», простирающийся на десятки обратных сан­тиметров (так называемое крыло линии Рэлея). Рассеяние света на флуктуациях ориентации молекул называют также анизотропным (деполяризованным) рассеянием. При макроскопическом описании можно считать, что анизотропное рассеяние вызывается нарушениями симметрии среды (ее изотропности), т. е. рассеяние происходит на флуктуациях симметрии. Общий вид рассеянного спектра, с учетом рассмотренных выше возбуждений вещества, представлен на рис. 6.4.

Взаимодействие света с ориентационными степенями свободы мо­лекул также является источником оптического ангармонизма, который проявляется в открытом еще в прошлом веке эффекте Керра (при этом Дя—'£(), оптическом эффекте Керра. и самофокусировке (Ап~\Е_г\^г), в эффекте вынужденного рассеяния на Крым линии Рэлея.

Оценим вклад ориентационного энгармонизма в кубичную воспри­имчивость. Рассмотрим сначала неполярную молекулу. В поле E(t) она приобретает индуцированный дипольный момент rf(fywa(<o).£(0 (поглощением пренебрегаем) и среднюю по времени энергию (см. (4.1.32)):

Ч*><= — Re£¹-¹-a-£^{l +} '. (6.2.81)

Следовательно, анизотропная молекула стремится повернуться относительно поля так, чтобы ее поляризуемость была максимальной.

Рис. 6.4. Основные виды рассеяния света, соответствующие им нелинейности и типичные частоты: 1 — температурное (энтропийное) рассеяние на флуктуация* температуры связано с электрокалорическим энгармонизмом (ДА—10^е с^-1); 2— рассеяние Мандельштама — Бриллюэна (Й~Ю^М с^-1) на флуктуациях давления связано со стрикционным энгармонизмом; 3 — крыло линии Рэлея вызывается флуктуациями анизотропии и связано с ориеатациовиым энгармонизмом (ДУ~ — i0ⁿ с^-1), 4— комбинационное (рамановское) рассеяние на внутренних колебаниях молекул {Q—Ю¹⁴ с^-1)- Первые три тала рассеяния объединяются терминами молеку­лярное или ps.ieeecK.oe рассеяние

Однако в равновесном веществе ориентации молекулы полем препят­ствует взаимодействие с соседями —- релаксационные процессы восста­навливают нарушенное полем равновесное состояние с хаотической ориентацией. В результате конкуренции между полем и тепловым дви­жением устанавливается динамическое равновесие со слабой степенью ориентации порядка ^Ч'иГ. При этом жидкость становится двупрелом-ляющей — подобной одноосному кристаллу с осью, параллельной Е (в случае линейной поляризации поля). Это явление называется опти­ческим эффектом Керра.

Пусть анизотропия поляризуемости характеризуется величиной Да(<о) (например, для линейной молекулы Аа=а_п—a _L—разность поляризуемостей вдоль и поперек молекулы). Тогда индуцируемое полем с частотой w_t изменение восприимчивости Д);(ш_г) на частоте <о₃ будет по порядку величины равно произведению Да(со_г) jV на степень ориентации:

АхдаДафО Да((о₂} N^tfixT. (6.2.82)

Итак, с точностью до числовых множителей для неполярных мо­лекул

Х™&Аа(а>Д Да(ш₂) NlxT. (6.2.83)

Полагая анизотропию сильной (Аажа=у}³4N), получаем

E%_L « _Х^а'/У.^ш « - (6.2.84)

Пусть а«й[1^10-^г,см³ и Г = 300 К, тогда E_NL = 2- 10^s Гс, и если Х^ш-=0,1, то х^ш=10-»см^а/эрг (ср. (12), (13), (37)).

Если у молекулы имеется постоянный динольный момент d„ и ориентирующее поле — статическое или медленно меняющееся за время ориентационной релаксации (х 10~¹² с), — то эффективная энергия равна У³= —d_aE (индуцированным моментом теперь можно пренебречь). При этом степень ориентации будет уже пропорцио- нальна так как линейный электрооптический эффект в жидкости запрещен (§ 6.1). В результате

Х^(э,(». —0, 0)«Да(ш)ЛГ((У)(Т)«~10-"см³/эрг₍ (6,2.85) E_NL at xT/d, ~ 10⁴ Гс (6.2.86)

(здесь принято а\ = 1 Д). Таким образом, эффект Керра в полярных жид­костях заметно больше, чем в неполярных.

Пусть теперь ориентирующее поле — оптическое бигармоническое, причем Я^зо^—t»₂-<!l/T, тогда "Р® и соответственно степень ориентации f³iy.T будут содержать переменную составляющую с частотой Q. В ре­зультате поляризации на частоте пробного поля <о_я (которая может и совпадать с nil или а₂) будет промодулирована, т. е. вещество будет излучать когерентное поле с частотами ю₃±Й. Таким образом, ориен­тационный энгармонизм дает резонансный вклад с шириной 2/т в ку­бическую восприимчивость %^U)((o_a, —ы₂, ш,) в области (ю,—ш₂)^1/т. При учете ориентационной релаксации этот вклад имеет мнимую часть, которая соответствует усилению поля ш_г с максимумом при (о₂ = =ш₁—1/т и приводит к эффекту вынужденного рассеяния на крыле линии Рэлея.

Количественно ориентационный ангзрмонизм описывается с по­мощью функции распределения молекул по ориентации, которая при Ят<^1 является стационарной:

^Р_{^{в)=Се-Г>ю = с\\-& + ±(%.у-...], (6.2.87)}

где С — нормировочный множитель (зависящий, конечно, от темпера­туры и поля), энергия "5^(9) определена в (81) ив-— совокупность трех углов, задающих ориентацию молекулы относительно лабораторной системы координат (углы Эйлера).

В случае неполярных молекул можно ограничиться линейным по 1/х7" разложением:

С = Р^ш(1 + <9°>^ш/кТ), Р (9) = Р^(о) [1 — {"У³ — <W')IkT], (6.2.88) где

_<^_><« = J &0Р^Ш9*, P^m = 1 /J <#Ю= 1/8л². (6.2.89)

Усредненный по углам индуцированный дипольный момент имеет вид

«/> - <а (0)> -£ + <р (9)> :ЕЕ+..- (6.2.90)

Угловые скобки означают усреднение с помощью возмущенной полем функции распределения P(Q). Если пренебречь внутримоле­кулярным энгармонизмом (В = 0), то <d> — а-Е, где

_аи<а(в)>= $^9Р(в)ее{в) =

= a^lr"^«a(6)^(e)>⁽⁰> —а»'<У>^№,)/к7\ (6.2.9))

а$ ^ J d'H^'a,* № = 8_аР (а^ + «,,„ + а„)/3 (6.2.92)

(к"¹¹ — усредненная по равновесной функции распределения линей­ная поляризуемость). Отсюда находим поправку к поляризуемости (подробнее см. [14}):

а—а^ш= J d³0[a(G) — a"'¹] Re£^l-'-a(6)-£^(+,/8n^1,x7'. (6.2.93)

Здесь a (0) —тензор линейной поляризуемости в лабораторной си­стеме координат для молекулы с заданной ориентацией 0.

При Qt^I надо учитывать изменение функции распределения во времени /^> = /^>(8, t), определяемое с помощью кинетического уравнения (см. [14]) или уравнения типа Фоккера—Планка. Эти уравнения в приближении экспоненциальной релаксации дают обычную дисперсионную зависимость с центром при и>₁ = а>₂:

_х«> (oj_s - w₂—_Ml + _Wl) ~ + / {со, — <*,) т]. (6.2.94)

Следовательно, компонента поля с меньшей частотой (стоксова) усиливается (у,^ш" <0), причем усиление максимально при |£3| = 1/т.

^:Квантовая теория нелинейной поляризации. Нелинейные поля­ризуемое! и 6, у, ... молекул и восприимчивости вещества ^^(а) ~ JVP. Х¹³' Л?у можно вычислить аналогично линейной поляризуемости (§ 4.2)—с помощью уравнения для матрицы плотности с феномено­логическими константами затухания. Проще, однако, воспользо­ваться общей формулой (3.3.36) для отклика </(()) квантовой си­стемы на внешнее возмущение с энергией y(t), добавив затуха­ние из общих соображений на конечной стадии расчета.

Нас интересует установившийся отклик системы на периодиче­ское возмущение, поэтому нижние пределы интегрирования в (3.3.36) следует приравнять —оо. Верхние пределы можно приравнять -[-со, если для учета принципа причинности добавить к подынтеграль­ному выражению ступенчатые функции 9(( — . .., Q(t_k_₁^t_k). Введем затухание, необходимое для установившегося режима и практически неизбежное в любой системе, полагая (рис. 6.5)

в(г)-в-«* (г>0), 6(0=0 (f<0), (6.2.95)

где е —некоторая положительная константа, которую впоследствии заменим на v_ran.

Полагая в (3.3.36) f = d_a и f³ = —d-e, получаем для индуци­рованного дипольного момента порядка к следующее выражение (см. также [7]):

^{<Ш>Ш = и/Щdt.-.-l dtfiit-tj ... е(*,_,_t}_k^)у,

хs_P{_Р[... [di(o, 4ш ■ ■ ■ >4Ш«0 ■ ■ • ^Е«_к(<*)■ <⁶'²'⁹⁶)

Здесь р — равновесный оператор плотности, а операторы d'_a(f) берутся в представлении взаимодействия. Подынтегральная функция в (96) зависит от k+\ временных аргументов, из которых, как легко прове-рить, лишь k являются независимыми. Эта тензорная функция назы­вается функцией отклика системы или ее функцией Грина (причинной и при t£>\ многовременной).

Пусть поле имеет дискретный спектр:

E(t)^E_pexp(—imJ)!2, ±2, .... (6.2 97)

р

тогда интегрирование в (96) проводится элементарно. Так, для k=l, находим

с

— Чд

2h

xр_яч № ехр (iw_nJ + u^A)--d!,?,) dg$ехр (itu„ J, + i<a_aJ)] =

2£ Wffln-*u»—'e

^{dS^i)^«Pt-'V)- (6-2-98)}

Здесь подразумевается суммирование по индексам состояний m, п и по декартовым индексам а, |5=х, у, z (которые иногда для компак ности пишем вверху), а также по частотному индексу р. Если для учета затухания заменить е на скорость затухания у_тЛ недиагональной ком­поненты матрицы плотности, то определяемая (98) линейная восприим­чивость Хав совпадает с (4.2.18).

Аналогично при fe=2 из (96) следует

t и

^{= — I dtl I ЛHK'i + »/i)t»С«-')1я}

x Р_пл {4Ж <04? ехр I/ (w_nJ + ш_тtt_t + w,„tj\ -b .. } -

.^p"" .(Л*.——r+ ■- нл«рНКт»,)Ч.

(6.2.99)

Здесь выписан вклад лишь первого из четырех слагаемых двойного коммутатора [ftf(f)> (2(^УЬ <*(*_а)], ^{так как} остальные различаются только знаками и перестановкой индексов состояний т, п.

Рассмотрим сложение частоты a>₁ + «_B=^<ilV При Wj^ox, в двой­ной сумме по частотам поля слагаемые, осциллирующие с частотой й)₀, встречаются два раза- при 0 = 1, /? = 2 И при 0 = 2, 0 = 1, по­этому «„-компоненту дипольного момента можно представить в виде суммы двух слагаемых, различающихся перестановкой индексов 1, у и 2, р\-

. - ^(я> ,ф> М» i

С = ■ ■■} (6.2.100)

(где

^{«V —'Yx.ii.}

П—опера юр суммирования по перес i ановкам и мы заменили е на -у_тя. Заметим, что дисперсионная функция I/O является фурье-об-разом ступенчатой функции 9(£) (рис. 6.5).

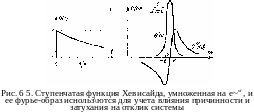Итак, квадратичная восприимчивость вещества, состоящего из N одинаково ориентированных невзаимодействующих молекул, выра­жается через не возмущенные населенности уровней Л'„ = р_нпЛ', час­тоты ai„,_n и моменты d_mn переходов следующим образом:

' П -1 \ л; / anm."miat_n . а_та a_mi Ufa

2h* «^рт^ 'Л *>№т

10) _П(1)

am

D&f' DUD.

(6.2.101)

где индексы 0 и 0 относятся к частотам +в_в,

Нетрудно убедиться, что выражение (101) обладает всеми свой­ствами симметрии, установленными в § 6.1. Оператор П обеспечи­вает частотно-пространственную симметрию по последней паре ин­дексов (6.1.14). Свойство (6.1.15) следует из = —и d*_mn = ~d„_n, так что изменение знаков всех частот и мнимой единицы лишь меняет местами слагаемые в (101) (первое со вторым, третье с четвертым).

Равенство нулю %^[2> в центросиммегричных средах также сле­дует из (101). Собственные состояния системы с центром инверсии имеют определенную четность: <р_и (—r) = ± ф„ (г), поэтому d_mn = 0, если ф_я и ср„ имеют одинаковые четности. Следовательно, хотя бы один из трех моментов, связывающих состояния U т, п, равен нулю.

Симметрия (6.1.20) в случае прозрачного вещества также сле­дует из (101) при у_тп=;0. При этом можно попарно объединить

последние слагаемые в (101):

1

]

' lit ^u run

В результате из 8 остаются 6 = 3! слагаемых, отличающихся перестановками пар индексов (а, 0), (В, 2), (у, 1):

V ТТ°^П

(6.2.102)

Восприимчивость следующего порядка вычисляется аналогичным образом. Каждый следующий порядок теории возмущения добав­ляет множители вида d_lnlhD%'. Отсюда следует оценка для опти­ческого энгармонизма в области прозрачности:

Я™^^»75^£о. (6.2.103,

где а„, ш₀, Е„-—характерные для молекулы размер, частота и внут­реннее поле. Для агома водорода Е_в= 13,6В/й₀ як 10^? Гс. Полагая Х^ш = 0,1, получаем _х«' = Ю~^в Гс~\ _хш₌ю~ч Гс~К Несмотря на грубость этой оценки, она дает верное представление о порядках величин. При резонансе %^ш соответственно возрастают.

"Вероятность многофотонных переходов. Если интересоваться лишь энергетической стороной вопроса, то нелинейное взаимодействие излучения с веществом можно описывать в терминах вероятностей или сечений многофотонных переходов (так, как это было сделано в гл. 2 для линейного однофотонного взаимодействия). При этом поле можно, как правило, не квантовать, т. е. использовать полукласснческую тео­рию, но результаты расчетов удобно трактовать на фотонном языке.

Найдем в качестве примера вероятность двухфотонного элементар­ного процесса, описывающего эффекты рамановского рассеяния и двухфотонного (индуцированного) поглощения или излучения. Под­ставив амплитуду перехода первого приближения (2.1.22) в уравнение (2.1.19в), получим для амплитуды двухфотонного перехода с уровня а на уровень Ъ:

t t,

_{cffi(0 = С*)*"' 5 S (6.2.Ю4)}

Здесь индекс n, по которому подразумевается суммирование, нумерует все промежуточные (виртуальные) невозмущенные состояния, посред­ством которых осуществляется переход. Это выражение отражает важ­ную особенность квантовой динамики — в переходах участвуют все возможные виртуальные состояния (с кажущимся нарушением законов сохранения) с единственным ограничением, следующим из принципа причинности: ^>(_г>^>/].

Подставим в (104) дипольное возмущение f^'——d'-Еи полигармо-яическое поле (97) (полагаем t„, (=±оо):

да ^3

— to — JJ

Вклад нижнего предела в интеграле по Ё_± исчезает за счет адиабатиче­ского включения возмущения или затухания (см. (95) при е-»-+0). Оставшийся в (105) интеграл является одним из представлений б-функ-

цин: jjfft₂...=2n6 —га_д— (й_р). Итак, поле возбуждает молекулу во втором порядке теории возмущений лишь при совпадении суммы (ал­гебраической) двух частот поля и частоты рассматриваемого перехода д-э-Ь. Это условие является обобщением постулата Бора для однофо-тонного резонанса.

Пусть две частоты поля со₍ и а₂ удовлетворяют условию «комбина­ционного» резонанса со1+«»_э;«со_йи, тогда из (105) имеем

с&> = i (2я/А) (£, ■ М^и- £,) 6 («_te—Шг-о>,), СЬС=-гУ I ^^-+- У (6.2.106)

п

Если со_йа>0 (т.е. исходное состояние молекулы — нижнее), то (106) определяет амплитуду процесса поглощения молекулой двух фотонов (при ©!, Юг>-0) или поглощения одного (ш!>*0) и рождения другого — стоксова — фотона (ю_а-<0). В последнем случае (106) яв­ляется амплитудой стоксова римановского процесса. Аналогично при <о_Ья<0 (106) определяет двухфотонное излучение или антистоксово рассеяние. Можно считать, что два слагаемых в (106) отличаются после­довательностью поглощения (или рождения) фотонов ©j и со_э.

Заметим, что возможны четыре варианта двухфотонного излуче­ния — вынужденное, спонтанно-вынужденное, вынужденно-спонтан­ное и чисто спонтанное (рис. 6.1, е). Этим процессам соответствуют че­тыре слагаемых в выражении ((Vi + l)(k_i-\-\)=NiN₂+N_l+N_i+], следующем из (106) при замене Е_р на операторы (здесь N_p— исходные числа фотонов).

Из (106) следует, что максимальный вклад в амплитуду перехода дают виртуальные состояния с минимальным дефицитом энергии h(io_aX—ю_р). Отметим, что различные «пути» перехода (т. е. вклады различных виртуальных состояний) могут отличаться знаками и по­давлять друг друга (квантовая интерференция состояний).

помощью двух ФЭУ и схемы совпадений. Подчеркнем, что спонтанное (а также тепловое) двухфотонное излучение, в отличие от однофотон-ного, имеет непрерывный спектр, не связанный с дискретным спектром невозмущенного атома. Статистика двухфотонного излучения нагре­того тела также существенно отличается от однофотонного, что свя­зано с тем, что фотоны излучаются парами. Таким образом, энгармо­низм вещества приводит, в принципе, к отклонению статистики теп­лового излучения от гауссовой [37].

Выводы. Итак, в оптический энгармонизм макроскопического ве- щества вносит вклад целый ряд механизмов. Квадратичная восприим- чивость у}^ связана, как правило, с нелинейностью связанных элект- ронов. Она отлична от нуля только в пьезокристаллах и имеет порядок Ю^-7—10^-э Гс^-1 при условии, что все частоты лежат в оптическом окне прозрачности. Кубическая восприимчивость %¹³¹ в конденсированном прозрачном веществе также вызывается электронной нелинейностью {X^I3,~1Q^_1S Гс^-2), если все частоты оптические. Если же разность двух частот Q совпадает с частотой молекулярных колебаний, то %^w воз- растает до 10~^,а— 10~^|а из-за смешанной электронно-ядерной (плаче- ковской или рамановской) нелинейности. При основной вклад

в случае твердых тел вносит электрострикция {%^lal~-10~^ia), в жидкос­тях к ней добавляется ориентационная (керровская) нелинейность Ю^-1-). Электрокалорический энгармонизм дает обычно х^1з)^ 'SIO^-13. Чрезвычайно сильные нелинейные оптические эффекты на­блюдают в жидких кристаллах и плазме. Отметим, что нелинейная электродинамика плазмы хороню описывается кинетическими урав­нениями Ландау — Власова (см. Г23!).