
- •Глава I
- •§ 1.1. Основные понятия квантовой электроники
- •§ 1.2. История квантовой электроники
- •Глава 2
- •§2.(. Амплитуда и вероятность перехода
- •§ 2.2, Переходы в монохроматическом поле
- •§ 2.3. Сечение и коэффициент поглощения
- •§ 2.4. Вынужденные переходы в случайном поле
- •§ 2.5. Поле в качестве термостата
- •2 Д. Н. Клышко
- •Глава 3
- •§3.1. Определение и свойства матрицы плотности
- •§ 3.2. Населенности уровней
- •§3.3. Эволюция матрицы плотности
- •Глава 4
- •§4.1. Определение и общие свойства восприимчивости
- •§ 4.2. Теория дисперсии
- •§4.3. Двухуровневая модель и эффект насыщения
- •§4.4°. Уравнения Блоха
- •Глава 5
- •§5.1, Вынужденные нестационарные эффекты
- •§ 5,3, Коллективное излучение
- •2T„ (нижний рисунок)
- •§ 6.1. Нелинейные восприимчивости — определения и общие свойства
- •§6.2. Модели оптического энгармонизма
- •§ 6.3. Макроскопическая нелинейная оптика
- •§ 6,4. Непараметрические взаимодействия
- •§ 6.5. Параметрические взаимодействия
- •Va? д. Н. Клышко
- •71 Д н Клышко
- •Глава 7
- •§7.1. Закон Кирхгофа для квантовых усилителей
- •§ 7.2. Основные понятия статистической оптики
- •§ 7.3. Гамнльтонова форма уравнений Максвелла
- •§ 7.4. Квантование поля
- •§ 7.5Ь. Возможные состояния поля и их свойства
- •0Онным11.
- •§ 7,6°. Статистика фотонов и фотоэлектронов
- •Уважаемые читатели!
§ 5,3, Коллективное излучение
Как уже отмечалось, характер излучения макроскопического вещества резко зависит от условий его возбуждения. При обычном хаотическом (некогерентном) возбуждении состояния отдельных атомов статистически независимы, вещество описывается диагональной матрицей плотности, и в результате мощность излучения линейно зависит от общего числа атомов N (полагаем, что линейные размеры образца много меньше длины пробега фотона: «/<^l). В случае же когерентного возбуждения все N атомов находятся в одинаковых состояниях и можно описывать образец общей волновой функцией. При этом, как легко убедиться с помощью полуклассической теории, & может зависеть от N квадратично, что должно качественно изменить картину. Ниже мы рассмотрим два необычных оптических эффекта, обязанных своим возникновением установлению квантовой когерентности в макроскопическом образце.
Эффект сверхизлучения. Пусть в начальный момент времени имеется /V одинаковых атомов, находящихся в независимых когерентных состояниях
Ь ={М>, + 1 2>у-ехр[- iЫ-Ь)])1У2. (5.3.1)
Это частный случай возможного состояния системы из N различимых (по координатам г,) частиц, когда волновая функция системы факторизована:
S =1
Найдем средний дипольный момент системы
<d> « Сф 12 dj ] д]з> = 2 <Ф/1 dj | %> = d„ 2 cos (»„/ + Ф/)> (5.3.3) i i i
ПО
считаем моменты перехода dc=d12 вещественными и ориентированными вдоль определенной оси. Здесь фаза когерентного состояния ф, для j-то атома имеет наглядный смысл — это фаза прецессионного движения вектора Блоха (при приготовлении состояния с помощью я/2-им-пульса она определяется фазой поля в точке нахождения атома г,). Если N=2, то согласно (3) амплитуда осцилляции общего дипольного момента удваивается при ф1=фа и обращается в нуль при ц>х—<р2=л. В случае N атомов с одинаковыми ф^ имеем
(d)=Ndecos((bot+tp).
Предположим далее, что линейные размеры системы много меньше длины волны, /<^с=2яс/ши, так что применима формула (5.2.3) для мощности дипольного излучения. Если заменить в ней (/кя на {d), то при одинаковых фазах получим !Р«„Г~№—мощность, излучаемая осциллирующими с одинаковыми фазами диполями, пропорциональна квадрату их числа. Этот эффект когерентного (коллективного, кооперативного) спонтанного излучения многоатомной системы называется сверхизлучением. Хотя его классическая интерпретация тривиальна, квантовая теория была впервые рассмотрена лишь в 1954 г. Дике Г7, 27].
Близкое по существу явление наблюдалось до этого в радиодиапа-зоне в экспериментах по ядерному магнитном} резонансу — ЯМР. При этом парамагнитный образец помещается внутри двух скрещенных катушек индуктивности (метод магнитной индукции). Резонансный ток в одной из катушек возбуждает вынужденную прецессию макроскопического магнитного момента образца М вокруг направления постоянного магнитного поля (см. (4.4.34)). Вращающийся момент М наводит во второй, приемной, катушке ЭДС индукции. В результате мощность наблюдаемого сигнала пропорциональна квадрату числа ядер в образце.
Когерентное излучение сфазированных диполей наблюдается и во многих эффектах нелинейной оптики типа генерации гармоник. Однако здесь, как и в явлении ядерной индукции, излучение происходит на частоте внешней силы, которая может в оптике сильно отличаться от собственных частот переходов. Существенно, что условие 1<^Х необязательно — при подходящем набеге фазы вынужденной или свободной прецессии вдоль какого-то направления, когда ф;=&г, (условие пространственного синхронизма), излучение в этом направлении будет когерентным (здесь k — волновой вектор и z;— координата /-го атома). Таким образом, сверхизлучение протяженных систем неизотропно, оно максимально в направлении синхронизма z г).
Полуклассический подход, использующий формулу (5.2 3) для мощности когерентного излучения с заменой dKn на <dy, дает точный результат лишь при N^>1. Напомним, что при N = 1 пришлось ввести дополнительный множитель 2 в формулу (5.2.4). Как уже говорилось выше, в общем случае надо вместо д?^ использовать нормально упорядоченный квадраг 2<d'~) d{+iy, что приводит
Мы уже встречали в § 5.1 пример такого явления — затухание свободной поляризации.
к замене Л/2 на N{N^-1): <d'-MlT)> =
- 2 «Г ч+,> - 2 <ь 1<*Г V I v -г 2 <% I <*,-> | %> <% 1 <*г I
= d! [ЛГ + 2 cos (<р,- - Фл) j /2 - dSW (Л' + 1 J/4. (5.3.4)
Подставляя (4) в (5.2.10), получаем следующее выражение для мощности сверхизлучения N атомов, находящихся в когерентных состояниях:
(5.3.5)
Последнее равенство в (4) предполагает равенство всех фаз фу— взаимную когерентность состояний.
Если же фазы прецессии являются независимыми случайными величинами, равномерно распределенными в интервале 0—2я, то все косинусы после усреднения обратятся в нуль и в (4) останутся лишь N диагональных слагаемых
5>иек0Г = К<4Л72.
(5.3.6)
Здесь буквенный индекс подчеркивает взаимную некогерентность излучения отдельных атомов, каждый из которых находится в когерентном состоянии на экваторе сферы Блоха.
Ясно, что кроме рассмотренных крайних случаев (4) и (6) возможно множество других состояний Л'-атомной системы. Б частности, как видно из приведенного выше примера для двух атомов, возможны безызлучательные состояния, когда коллективные эффекты подавляют дипольное спонтанное излучение.
При учете теряемой на излучение энергии спонтанное сверхизлучение будет быстро затухать. Длительность импульса сверхизлучения можно оценить, разделив запасенную системой энергию %etuN!2 на начальную мощность когерентного излучения (5):
TlwrJ*2M(A4-l). (5-3.7)
Итак, при Л^>1 и 1<^Х излучательное время жизни когерентного состояния И•атомной системы сокращается в N12 раз вследствие коллективного эффекта. Однако, как уже отмечалось, в протяженных системах сверхизлучение направленно, т. е. эффективно «работает», забирает энергию лишь часть мод поля, и поэтому тиог возрастает (примерно в 4л/Д£3 раз, где AQ — эффективный телесный угол, в который происходит излучение). При вытянутой форме образца с числом Френеля аг/К1—-\ это замедление сверхизлучения имеет порядок (а/Л)а~/Л^>1, где а2— сечение образца, I — длина.
Рассмотрим теперь случай энергетического начального состояния JV-атомной системы: г|э (0) =П 12h. Вектор Блоха каждого атома направлен вверх, на северный полюс. В первые моменты времени атомы нзлуцают независимо,
5>~2<Ч>|#-М1 '\^>=Ndl (5.3-8)
и постепенно переходят из энергетического состояния в когерентные с какими-то углами и фазами tpy прецессии.
 Однако
можно ожидать, что атомы влияют друг
на друга через поперечное поле, и поэтому
фазы прецессии должны взаимно
синхронизоваться (при достаточной
плотности атомов [30]). В результате
через какое-то время задержки U
система
самопроизвольно перейдет в сверхиз-лучающее
когерентное состояние со сфазирова
иными диполями. В этот момент медленное
спонтанное излучение перейдет в
короткий мощный импульс сверхизлучения
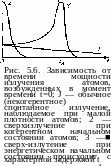
с определенной фазой поля (рис. 5.6).
Однако
можно ожидать, что атомы влияют друг
на друга через поперечное поле, и поэтому
фазы прецессии должны взаимно
синхронизоваться (при достаточной
плотности атомов [30]). В результате
через какое-то время задержки U
система
самопроизвольно перейдет в сверхиз-лучающее
когерентное состояние со сфазирова
иными диполями. В этот момент медленное
спонтанное излучение перейдет в
короткий мощный импульс сверхизлучения
с определенной фазой поля (рис. 5.6).
Аналогия с фазовыми переходами. Последовательная теория, а также эксперимент (см. [30]), впервые проведенный в 1973 г., подтверждают рассмотренную качественную картину. Часто именно этот удивительный эффект называют сверхизлучением. Спонтанное установление упорядоченного когерентного состояния из хаотического состояния в макросистемах вообще представляет большой интерес для физики. Отметим аналогию между процессом спонтанного формирования сверхизлучающего состояния в системе возбужденных атомов и фазовыми переходами в равновесном веществе. Другой пример такого фазового перехода в неравновесной системе— установление автоколебаний с определенной фазой и макроскопической амплитудой при достижении порога в лазере [32, 50, 52]. Здесь также в результате взаимодействия атомов (через поле резонатора) хаотическое шумовое поле Сменяется упорядоченным и устанавливается регулярная переменная макроскопическая поляризация. Заметим, что в равновесных системах причиной фазовых переходов также является взаимодействие атомов или молекул через поле, но только статическое. Грубое описание сег-нетоэлектрического перехода дает модель Лоренца — согласно (4.2.11) при достаточной плотности атомов частота резонанса поляризации обращается в нуль. При этом восприимчивость на нулевой частоте стремится к бесконечности и в системе самопроизвольно устанавливается макроскопическая статическая поляризация.
Сверхизлучение в инвертированной системе следует отличать от сеерхлюяинесценции (стационарной или импульсной) — усиленного спонтанного излучения (§7.1). В режиме сверхлюминесценции процессы безызлучательной релаксации (например, столкновения в газах, взаимодействие с фононами в твердых телах) препятствуют установлению когерентности в макроскопических объемах, и поэтому излучении определяется числом частиц в первой, а не второй степени.
Оптическое эхо. В случае неоднородного ушнрения различные атомы имеют слегка различные собственные частоты (из-за эффекта Доплера, неоднородных статических полей и др.). При этом наблюдаемая ширина линии A(i>5=2<Tj какого-либо перехода много больше столкно-вительной или радиационной ширины 2/Та.
I(t) |
|
|
|
1 ! |
|
|
|
1 1 ] \ 1ь |
• |
! ! |
|
0 |
г/ |
/ *» \ |
|

Рис. 5.7. Эффект оптического эхо. После возбуждения вещества двумя короткими световыми импульсами (штриховые линии на верхнем рисунке) оно излучает вспышку света (сплошная линия) спустя время ta, равное интервалу между импульсами. Эффект объясняется совладением фаз колебаний зарядов отдельных молекул в момедт
