57. Что такое общая ошибка первого рода для набора тестов?

Количество тестов в некотором их наборе определяется исходя из так называемой общей ошибки 1-го рода, т.е. той части случайных последовательностей, которые не пройдут хотя бы один из тестов.

Общая ошибка 1-го рода вычисляется для заданных ошибок 1-го рода каждого из тестов при условии их независимости. Если для всех тестов задано одно значение α, то вероятность того, что случайная последовательность не пройдет, по крайней мере, один тест из набора равна , поскольку быстро растет с уменьшением α .

Для выбранной величины A количество тестов определяется как из соотношения A ≈ 1 – е^-nα.

58. Почему для набора тестов необходима проверка их независимости?

Важным фактором «объективного» тестирования, является независимость тестов. Для проверки их независимости используется k “эталонных” последовательностей S₁,…,S_k, полученных, например, с использованием физических датчиков случайных чисел. Величина k должна быть достаточной ( k ≥ 500) для применения критерия независимости 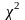вида

59. Как устроен линейный конгруэнтный генератор ррсп?

Наиболее простым программным датчиком псевдослучайных чисел является линейный конгруэнтный генератор (ЛКГ), который описывается рекуррентным уравнением вида ,

где X₀ – случайное начальное значение, a – множитель, b – приращение, N – модуль.

Период выходной последовательности такого генератора не превышает N, максимальное значение достигается при правильном выборе параметров a,b,N , а именно, когда:

– числа N и b взаимно просты: НОД(N,b) = 1;

– a – 1 кратно любому простому p , делящему N ;

– a – 1 кратно 4, если N кратно 4.

60. Как функционирует регистр сдвига с линейной обратной связью?

Регистры сдвига с линейной обратной связью (Linear Feedback Shift Registers – LFSR) включают собственно регистр сдвига и схему вычисления функции обратной связи (tap sequence)

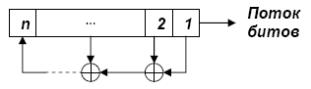
Теоретически, n-битный LFSR может сгенерировать псевдослучайную последовательность с периодом 2ⁿ–1 бит. Такие LFSR называются регистрами максимального периода.

Для этого регистр сдвига должен побывать во всех 2ⁿ – 1 ненулевых внутренних состояниях.

Одна и та же рекурента может быть сгенерирована регистрами разной длины. Предположим, что среди подобных регистров наш n-битный LFSR обладает минимальной длиной.

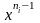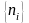Функции обратной связи регистра можно сопоставить полином m(x) степени не выше n с коэффициентами из поля вычетов по модулю два, состоящий из одночленов вида , где - множество номеров точек съема обратной связи.

61. Что такое линейная сложность последовательности?

Среди всех таких регистров, существует регистр минимальной длины L.

Величина L называется линейной сложностью последовательности S .

Напомним, что полином называется неприводимым, если он не может быть выражен как произведение двух полиномов меньшей степени, отличных от констант.

62. Какие критерии качества для выходных последовательностей криптографических генераторов выдвинуты Рюппелем?

1.Большой период выходной последовательности, отсутствие повторений.

2. Высокая линейная сложность, как характеристика нашего генератора через регистр LFSR минимальной длины, который может сгенерировать такой же выход.

3. Неотличимость от РРСП по статистическим критериям.

4. Перемешивание: любой бит ключевого потока должен быть сложным преобразованием всех или большинства бит начального состояния (ключа).

5. Рассеивание: избыточность во всех подструктурах алгоритма работы генератора должна рассеиваться.

6. Критерии нелинейности преобразований: в соответствии с некоторой метрикой расстояние до линейных функций должно быть достаточно большим; требуется лавинообразное распространения ошибок в случае изменения одного бита аргумента и др.