6.2. Основная теорема статики (общие условия равновесия системы сил)
Теорема. Для того, чтобы тело под действием системы произвольно расположенных сил находилось в равновесии необходимо и достаточно, чтобы главный вектор и главный момент относительно некоторого полюса этой системы сил были равны нулю.
6.3. Аналитические условия равновесия произвольной системы сил (шесть уравнений статики абсолютно твердого тела)
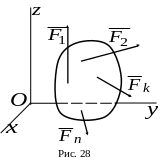Пусть
на твердое тело, находящееся в равновесии,
действует система сил
(рис. 28).
Выберем произвольную систему координат и обозначим проекции сил на оси координат:
,
,
.
Главный вектор этой системы сил:
.
Его проекции на оси координат:
,
,
.
Главный момент вычислим относительно полюса, находящегося в начале координат:
.
Главный момент относительно полюса в начале координат проектируем на каждую из осей координат:
.
На основании теоремы о связи между моментами силы относительно полюса и оси:
,
,
.
По основной теореме статики для равновесия тела под действием произвольной системы сил необходимо и достаточно, чтобы были равны нулю главный вектор и главный момент относительно произвольного полюса, то есть
, (I) 
, (II)
Векторное равенство (I) эквивалентно трем скалярным:
,
,
.
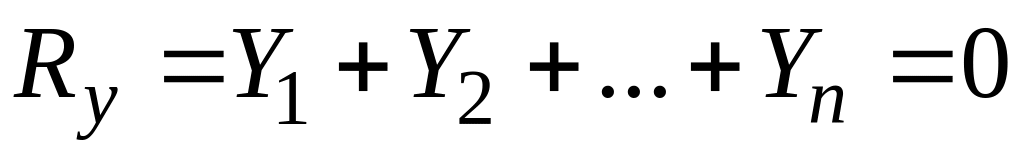Векторное равенство (II) так же эквивалентно трем скалярным:
,
,
.
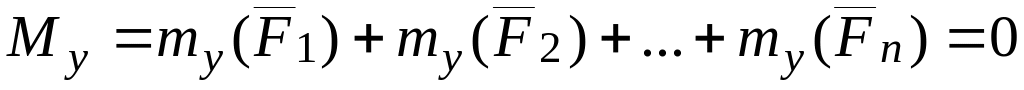На основании полученного результата основная теорема статики может быть сформулирована так:
Для того, чтобы твердое тело под действием произвольной системы сил находилось в равновесии необходимо и достаточно, чтобы сумма проекций всех сил на каждую из осей координат и сумма моментов всех сил относительно каждой из осей координат равнялась нулю, то есть чтобы выполнялись шесть уравнений статики:
1.
, 4. 
,
2.
, 5. 
,
3.
, 6. 
.
6.4 Частные случаи аналитических условий равновесия
1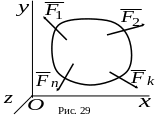
.
Плоская система произвольно расположенных
сил (все силы лежат в одной плоскости).
Выберем оси
координат так, чтобы оси
и
лежали в плоскости сил (рис. 29). В этом
случае из шести уравнений статики 3-е,
4-е, 5-е удовлетворяются тождественно.
Уравнениями равновесия являются три:
1. ,
2. ,
3. .
Для того, чтобы тело под действием плоской системы произвольно расположенных сил находилось в равновесии, необходимо и достаточно, чтобы выполнялись три уравнения статики: два уравнения проекций на оси, лежащие в плоскости сил и дно уравнение моментов относительно оси, перпендикулярной плоскости сил.
Плоская система параллельных сил.
О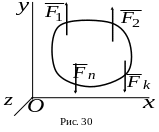
си
координат выбираем так, чтобы оси
и
лежали в одной плоскости с силами, причем
ось
параллельна силам (рис. 30). Это частный
случай произвольной плоской системы
сил. Из трех уравнений произвольной
плоской системы сил первое выполняется
тождественно, а уравнениями равновесия
остаются следующие два:
.
.
Для того, чтобы тело под действием плоской системы параллельных сил находилось в равновесии, необходимо и достаточно, чтобы выполнялись два уравнения равновесия: уравнение проекций на ось, параллельную силам и уравнение моментов относительно оси, перпендикулярной плоскости сил.
3. Пространственная система параллельных сил.
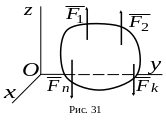Выберем
оси координат так, чтобы ось
была параллельна силам. В этом случае
из шести уравнений статики 1-е, 2-е, 6-е
удовлетворяются тождественно, а
уравнениями равновесия остаются
следующие три:
1. ,
2. ,
3. .
Для того, чтобы тело под действием пространственной системы параллельных сил находилось в равновесии, необходимо и достаточно, чтобы выполнялись три уравнения статики: уравнение проекций на ось, параллельную силам и два уравнения моментов относительно осей, перпендикулярных силам.
4. Система сходящихся сил.
Выберем начало координат в точке схода (рис. 32) Так как моменты сил относительно осей координат равны нулю, то уравнения 4,5,6 выполняются тождественно. А уравнениями равновесия остаются первые три (они уже были получены ранее).
1. , 2. , 3. .
4
.
Плоская система сходящихся сил.
Линии действия
всех сил пересекаются в точке
,
и все силы лежат в плоскости
(рис. 33). Уравнениями равновесия такой
системы являются:
,
. ,