1.7 Математикалық үміт және кездейсоқ шаманың дисперсиясы

1.7.1 Математикалық үміт.

Бақылау нәтижелері өлшеніп жатқан шаманың шын мәнінің айналасына шоғырланады, және ол мәнге жақындаған сайын, табу ықтималдығы арта түседі. Демек, өлшеніп жатқан шаманың шын мәнінің бағасы ретінде үлестірілу қисығы мен абсцисса осі арасындағы фигураның ауырлық центрінің координатасын алуға болады. Оны бақылау нәтижелерінің математикалық үміті деп атайды.

М[Х] =m_x= х ƒ(х)dx. (1.16)

Енді кездейсоқ қателіктің дәлірек анықтамасын былай беруге болады:

δ=Х - М[Х] (1.17)

(кездейсоқ қателік бақылаудың бірлік нәтижесі мен математикалық үмітінің айырмасына тең).

Сонымен, математикалық үміт – Х кездейсоқ шаманың шын орта

мәніне

тең (Х_ц=М[Х]) және үлестірілудің “ауырлық центрін” сипаттайды.

1.7.2 Бақылау нәтижелерінің үлестірілу дисперсиясы.

Бақылау нәтижелерінің үлестірілу дисперсиясы кездейсоқ қателіктертің үлестірілу дисперсиясына тең, және ол кездейсоқ қателіктердің математикалық үміт айналасында шашырауын сипаттайды. Яғни, кездейсоқ үлестірілудің “ауырлық центрі” айналасында орналасуын сипаттайды.

D[X] =D[δ] = 䲃(δ)dδ, (1.18)

D[X] = (х-М[х])² ƒ(х)dx. (1.19)

Механикалық интерпретация бойынша бақылау нәтижелерінің математикалық үміті үлестірілу қисығы мен ОХ осі арасындағы фигураның ауырлық центрінің абсциссасы, ал үлестірілу дисперсиясы ауырлық центрі арқылы өтетін вертикаль ось айналасында айналу инерциясы моментінің аналогы болып табылады.

1.7.3 Бақылау нәтижелерінің орташа квадраттық ауытқы.

Кездейсоқ қателіктер шашырауын сипаттау үшін диспериядан алынған түбірдің оң мәнін қолданады. Оны бақылау нәтижелердің орташа квадраттық ауытқуы деп атайды

=+ . (1.20)

Егер Z=х+y; х,у – тәуелсіз кездейсоқ шамалар болса, онда тәуелсіз кездейсоқ шамалардан бақылау нәтижелерінің орташа квадраттық ауытқуы (О.К.А.) былай анықталады:

= . (1.21)

1.8 Кездейсоқ шамалардың (қателіктердің) үлестірілулерінің түрлері

Қателіктердің үлестірілуінің түрлері өте көп. Мысалы, тек қана электрлік және электрлік емес шамаларды әртүрлі аспаптармен өлшеу қателіктерінің өзінде 217 үлестірілудің түрі бар. Мысалы, трапециялық, экспоненциялдық, Стьюдент үлестірілуі т.б. Солардың ішінде біздің қарастыратынымыз:

а) бірқалыпты үлестірілу;

ә) қалыпты үлестірілу (Гаусс үлестірілуі);

б) Стьюдент үлестірілуі.

1.8.1 Бірқалыпты үлестірілу.

Кездейсоқ шаманың мүмкін болатын мәндері, немесе өлшеу құралдарының кездейсоқ қателіктерінің мүмкін болатын мәндерінің ықтималдықтары бірдей болып, [а,в] интервалында жататын болса, үлестірілу бірқалыпты деп аталады.

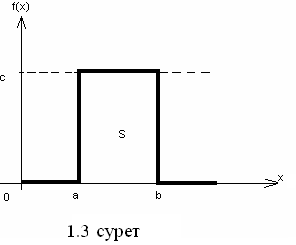Онда тығыздық функциясы ƒ (х)

былай анықталады:

ƒ(х) = {0, егер х<а болса,

{с, егер а ≤х≤в болса, (1.22)

{0, егер х>в болса

мұндағы с = .

Қ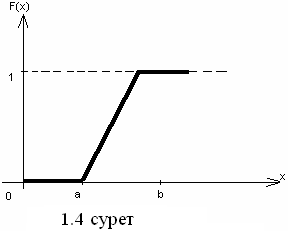 алыптандыру ережесі бойынша ƒ(х)dx=1, немесе ƒ(х)dx =1, яғни S=1.

Енді Ғ(х) интегралдық үлестірілу

функциясын анықтайық.

{ 0, егер х<а болса,

Ғ(х)={ , егер а≤х≤в болса, (1.23)

{ 1, егер х>в болса.

Бірқалыпты үлестірілген шаманың математикалық үміті былай анықталады:

. (1.24)

Сонымен математикалық үміт анықтамада айтылғандай берілген интервалдың ортасына сәйкес келеді (Х_ц=М[Х]).

Бірқалыпты үлестірілген шаманың дисперсиясы былай анықталады:

. (1.25)

Бірқалыпты үлестірілген шаманың орташа квадраттық ауытқуы:

. (1.26)

1.8.2 Қалыпты үлестірілу (Гаусс үлестірілуі).

Қалыпты үлестірілу (Гаусс үлестірілуі) ықтималдық теориясы мен математикалық статистиканың негізгі үлестірілуі болып табылады. Ол кездейсоқ шамалардың қасиеттерін өте жақсы ашады. Эксперименттік нәтижелерді өңдеу мен өлшеу қателіктерін бағалау үшін кеңінен қолданылады. Оның себебі орталық шектік теоремамен түсіндіріледі. Бұл теореманы тағайындауға ірі математиктер А.ДеМуавр, П.ДеЛапас, К.Ф.Гаусс, П.Л.Чебышев, А.М.Ляпуновтар еңбек сіңірген. Бұл теорема бойынша бақылау нәтижелерін құрайтын тәуелсіз әсерлесетін өте көп факторлардың әрқайсысының әсері қалғандарының соммалық әсерінен кем болса, кездейсоқ қателіктердің үлестірілу қалыпты болады.

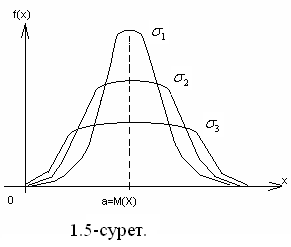
Қалыпты үлестірілудің дифференциял функциясы мына теңдеумен беріледі:

ƒ(х) = (1.27)

мұндағы х – [- ,+ ] интервалында берілген кездейсоқ шама мәндері;

а = М[х];

²=D[х];

>о – қалыпты үлестірілген шаманың стандарт ауытқуы.

Қалыптандыру ережесі бойынша

ƒ(х)dx=1

а=М[х] – тің бірдей мәндерінде

< ₂< болған жағдайда графиктердің

аудандарына қарасақ, артқан сайын

график «жайыла» түседі.

ƒ(х) =Ғ¹(х)болғандықтан, F(х) = ƒ(х)dx. Демек

Ғ(х) = ехр dx. (1.28)

Оң жақтағы интеграл ықтималдықтар интегралы деп аталады (қателіктер интегралы). Ол жақсы зерттелген, мәндері кестеленген. Есептеулер кезінде қалыптандырылған үлестірілу қолданылады, ол үшін өлшем бірліксіз аргумент енгізіледі

t= ; dx= , (1.29)

ƒ(t)= , (1.30)

Ғ(t) = . (1.31)

Бұл функция мәндері де кестеленген. Оның көмегімен қалыпты заң бойынша үлестірілген шаманың өлшеніп жатқан мәнінің берілген интервалға түсуінің ықтималдығын есептейді.

t стандарт ауытқу – ның үлесімен берілген. Ол Х шаманың а =М [Х] математикалық үміттен ауытқуын көрсетеді.

П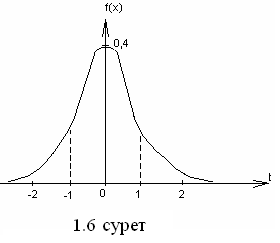 араметрлері М [Х] =а, болатын кез келген қалыпты үлестірілуге параметрлері (0,1) интервалында қалыптандырылған үлестірілу сәйкес келеді.

t (0) = .

Эксперименттік мәліметтерді өңдеу үшін

Лапластың қалыптандырылған функциясын

қолданған ыңғайлы.

Ф(t₁) =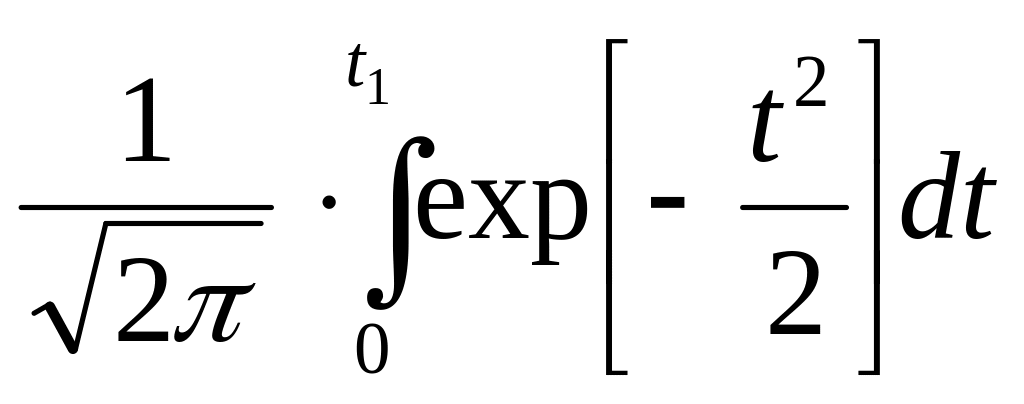 . (1.32)

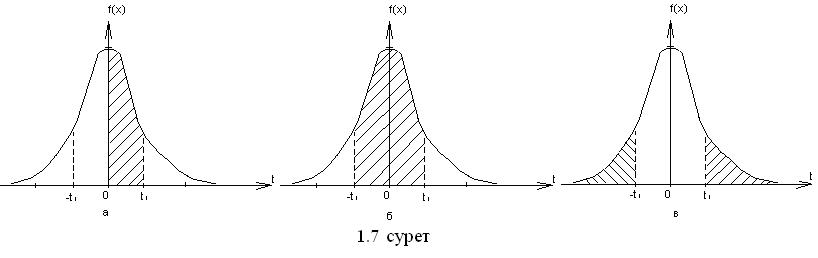
Р =Ф(t₁} (1.7а cурет), Р{- t₁<t<t₁}=2Ф(t₁) (1.7б cурет),

Р{t<-t₁;t>t₁}=1-2Ф(t₁) (1.7в cурет).

t=1 δ=± Ф(1) =0,34 Р{-1 < t < 1}= = 0,68|68%,

t=2 δ=±2 Ф(2) =0,477 Р{- 2 < t < 2}= 0,954|95%,

t=3 δ=±3 Ф(3) =0,4986 Р{- 3 < t < 3}= 0,997|99%.

δ=±3 ауытқу кезіндегі қателік өрескел қателік болып табылады, оны ары қарай өңдеуден алып тастайды. Бұл «3 ережесі» деп аталады.

1.8.3 Стьюдент үлестірілуі.

Бір физикалық шаманы көп рет (30 дан артық) бақылаулар арқылы анықтау кезінде қалыпты үлестірілуді қолдану заңды. Бірақ тәжірибе жүзінде 20-30 бақылаулармен шектелуге тура келеді. Бұл жағдайда үлестірілу заңы ерекше және бақылау санына тәуелді болады. Бақылаулар саны шектеулі болғанда, кездейсоқ қателіктерді Стьюдент (В.С. Госсет) үлестірілуі дәлірек сипаттайды. ƒ(х) тығыздық функциясы кездейсоқ қателікке ғана емес, сонымен қатар п – бақылау санына да тәуелді болады.

Аналитикалық түрде Стьюдент заңы мына теңдеумен өрнектеледі

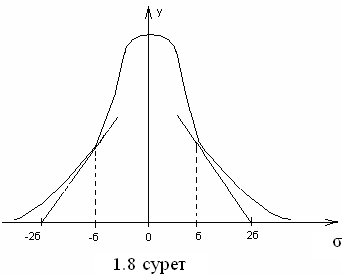
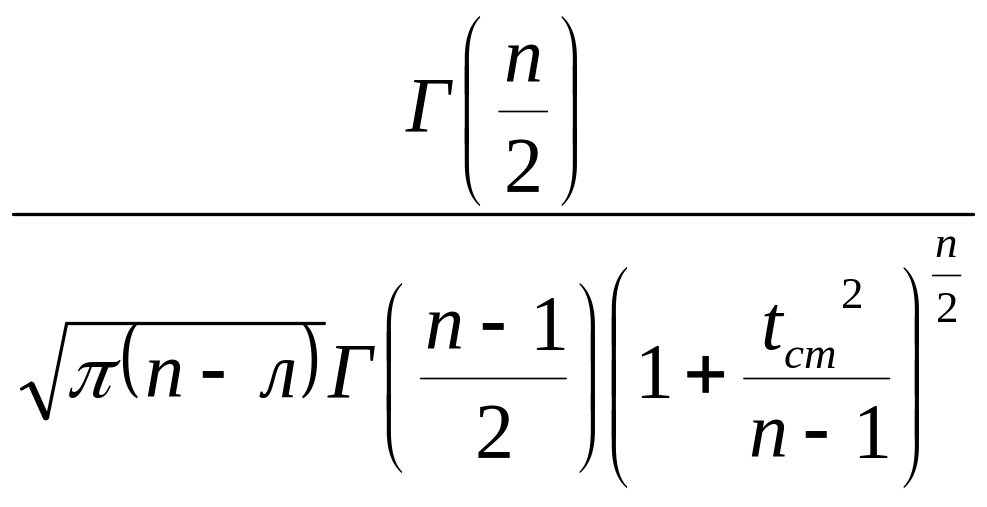ƒ( ,п) = . (1.33)

мұндағы Г(п) - гамма функция бүтін сандар үшін төмендегідей қасиеттерге ие:

Г(п +1)= п Г(п) және Г(п +1) = п! (1.34)

Стьюдент үлестірілуін сипаттайтын теңдеу

у= . (1.35)

Мұндай теңдеумен берілген қателіктер үлестірілуінің қисығы 1.8 суретте келтірілген. Оның төмендегідей қасиеттері бар:

а) қателіктер қисығы абсцисса осінен жоғары жатады, себебі – ның ешқандай мәнінде y-тің мәрдері нөлге және теріс мәнге тең болмайды;

ә) қисық оy осіне қатысты симметриялы, себебі exp – жұп функция;

б) =0 жағдайда y максимал мәніне ие болады;

в) нүктелері графиктің иілу нүктелері болып табылады;

г) иілу нүктесінен тұрғызылған жанама абсцисса осінен –ге тең кесінді қияды.

Метрологиялық жұмыстарда кездейсоқ шама мәндерінің берілген ықтималдықпен төмендегідей интервалдарға түсуіне көп көңіл бөледі.

δ=0 Р=1

δ=± Р=0,683

δ=±2 Р=0,954

δ=±3 Р=0,9973

«3 ережесі» бойынша қалыпты үлестірілген кездейсоқ шаманың ±3 интервалы шектерінен шығып кетпейтіндігінің ықтималдығы бірге жақын (Р=0,9973).

1.8.4 Сенімділік интервалы туралы ұғым.

Эксперимент нәтижелерін статистикалық өңдеу жолымен алынған бағаның сенімділігі жөнінде сөз болғанда, мынадай мәліметтерді білу керек:

- өлшеніп жатқан шаманың шын мәні анықталатын жинақтың көлемі жеткілікті үлкен ба?

- зерттеліп жатқан құбылыстың кездейсоқтығы мен кездейсоқ қателіктердің болуы салдарынан нәтиженің шашырау дәрежесі жоғары ма?

Мұндай информацияны біле отырып, өрескел қателіктерді анықтауға және өрескел қателіктері бар нәтижелерді ары қарай өңдеуден алып тастауға болады. Өлшеніп жатқан шаманың күтілген мәнін сипаттайтын – орташа арифметикалық мәнді және өлшеніп жатқан шаманың орташа мәнге қатысты шашырауын сипаттайтын – орташа квадраттық ауытқуды білу арқылы өлшеніп жатқан шаманың шын мәні жататын интервалды табуға болады.

Өлшеу нәтижесінің көбісі осы интервалда жатады. Бұл интервалдың орны мен ауқымын өлшеуді қанағаттандыратын ықтималдықтың мәнімен байланыстыра қарастырудың мағынасы үлкен. Бұл ықтималдық таңдалған интервалдың және алынып жатқан өлшеу сериясының сенімділігін сипаттайды.

Математикалық статистикада қолданылатын сенімділік интервалы дегеніміз өлшегенін жатқан шаманың мәні берілген ықтималдықпен табылатын интервал.

Өлшеніп жатқан Х шаманың үлестірілу функциясы Ғ(х) белгілі болса, Х тің мәндері ( - ; + ) интервалында болатындығының ықтималдығын сенімділік ықтималдығы деп атайды.

Р{ - < Х < + }=Ғ( + )-Ғ( - ) = (1.36)

мұндағы – n өлшеулердің орташа арифметика мәні;

– сенімділік ықтималдығы; 1-Р=q – мәнділік деңгейі болады.