1.5 Кездейсоқ шама

Кездейсоқ шама – бірдей жағдайларда өлшенген физикалық шаманың бір өлшеуден екінші өлшеуге өткенде, еріксіз өзгеріп отыратын мәні.

Олар дискретті және үздіксіз болып бөлінеді. Дискертті кездейсоқ шамалардың мүмкін болатын мәндері де дискретті (арасында сан жоқ нақты мәндер). Үздіксіз кездейсоқ шамалардың мәндері берілген интервалға үлестірілген болады. Мысалы: [а, b] ; [0, ] ; [- ,+ ] т.с.с.

– Х, Y кездейсоқ шамалардың мүмкін болатын мәндері.

Егер Х кездейсоқ шама үздіксіз үлестірілген болса, онда оны [х, х+Δх] интервалында табу ықтималдығы интервал көлеміне тәуелді болады.

Р{х ≤ Х ≤ х+ Δх }≈Δх. (1.7)

Х кездейсоқ шаманың мәні х мәнге ие болу ықтималдығы нолге тең

Р{Х = х }=0. (1.8)

Егер үздіксіз кездейсоқ шама [- ,+ ] нақты осьтің бәріне үлестірілген болса, онда интегралдық функцияны қарастыру керек.

Үздіксіз кездейсоқ шамалардың ықтималдығын анықтау үшін мүмкін болатын мәндердің шекті интервалын, немесе көлемі нолге ұмтылатын интервалдарды қарастыру қажет.

1.6 Үлестірілу функциялары және кездейсоқ шама ықтималдықтарының тығыздығы

1.6.1 Үлестірілудің интегралдық функциясы.

Х кездейсоқ шаманы бақылау нәтижесінің үлестірілуінің интегралдық функциясы Ғ(х) дегеніміз і-ші тәжірибеде бақылау нәтижесінің х_і мәні қандай да бір х-тен кіші болуы ықтималдығының сол х мәніне тәуелділік функциясы

Ғ(х)=Р{ х_і ≤ х }=Р{- х_і ≤ х } (1.9)

Ғ(х) функциясы төмендегі шарттарды қанағаттандырады:

а) Ғ(- )=0; Ғ( )=1. Яғни Ғ(х) функциясы мәндерінің өзгеру интервалы [0,1]. Ғ( )=1, демек кездейсоқ шаманың кез-келген мәнін нақты осьте табуға болатындығының ықтималдығы – нақты орындалатын оқиға;

ә) х₂ х₁ болса, Ғ(х₂) Ғ(х₁), демек ол өспелі функция;

б) Егер кездейсоқ шаманың мүмкін болатын мәндері [а, b] интервалында орналасқан болса, онда

{Ғ(х) =0, х≤а

{Ғ(х) =0, х≥в.

Ғ(х) – үздіксіз функция болғандықтан, оны дифференциалдауға болады;

в) Кездейсоқ шама мәндерінің [х, х+Δх] шекті интервалда табылатындығының ықтималдығы

Р{х≤Х≤х+Δх}=Ғ(х+Δх)-Ғ(х), (1.10)

егер Δх→0, р→0.

1.6.2 Үлестірілудің дифференциал фукциясы.

Үлестірілудің дифференциал фукциясы, немесе кездейсоқ шама ықтималдықтарының үлестірілу тығыздығы кездейсоқ шаманың қасиеттерін сипаттау үшін қолданылады.

Үлестірілудің дифференциал фукциясы өзінің аргументі бойынша интеграл функциядан алынған туынды функция болып табылады

ƒ(х) = . (1.11)

Үлестірілудің дифференциал функциясының графигін үлестірілу қисығы деп атайды. Ол қоңырау кейіптес болады (1.1а cурет).

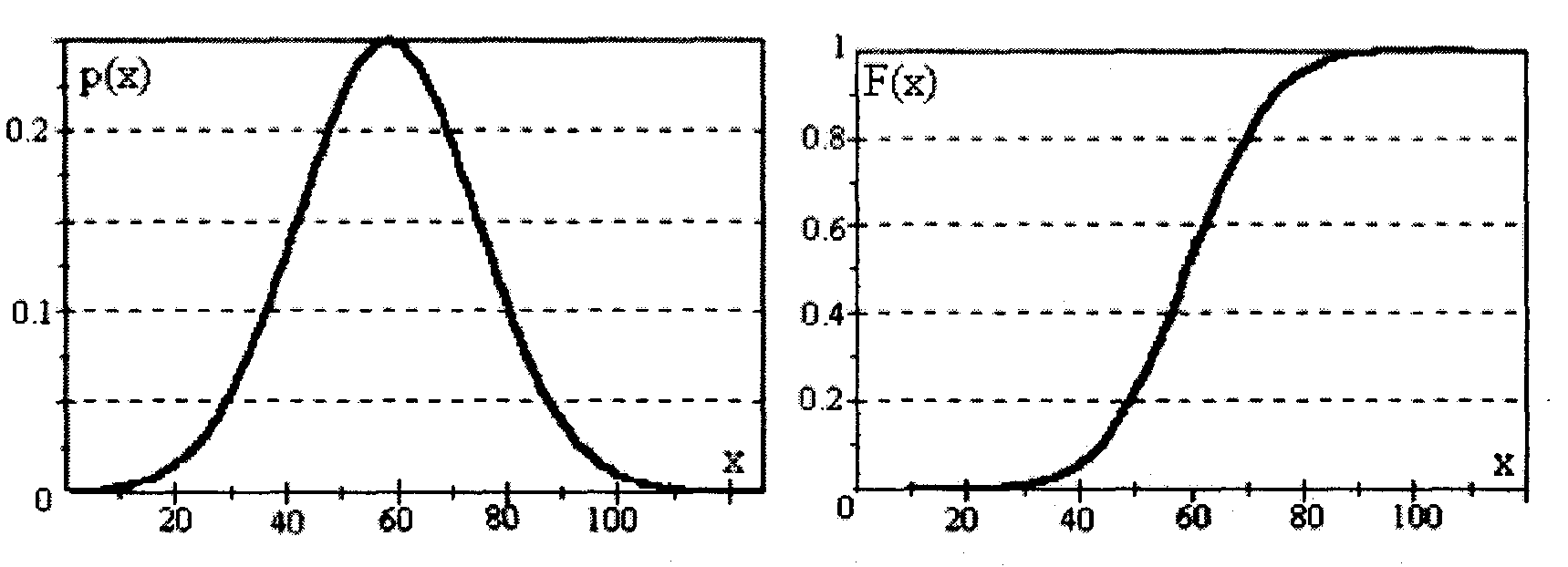
а) б)