105 Г лава 7. Момент силы и момент импульса

Глава 7. Момент силы и момент импульса

7.1. Момент силы относительно неподвижной точки и неподвижной оси

Рис. 7.1.

Выберем в инерциальной системе отсчета неподвижную точку . Обозначим через радиус-вектор, проведенный из точки к точке приложения силы , рис.7.1. Моментом силы относительно точки называется векторное произведение:

. (7.1)

Точку , относительно которой определяется момент силы, называют началом. Размерность момента силы в системе СИ равна .

Пример 7.1. Вычислим момент силы , приложенной к точке , относительно точки . Имеем: , , где и - радиусы-векторы точек и , проведенные к ним из начала системы координат. Радиус-вектор , проведенный из точки к точке , равен разности . Получим . Пользуясь формулой (7.1), находим в соответствии с правилом вычисления векторного произведения (см. подраздел 2.10):

.

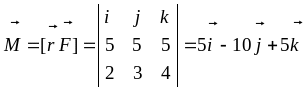Покажем, что момент силы не изменится, если точку приложения силы перенести вдоль линии действия силы. Обозначим через момент силы , приложенной к точке , рис.7.1. Через обозначим момент этой же силы, но приложенной к точке , лежащей на линии действия силы . Имеем:

,

где - радиус-вектор, проведенный из точки к точке ; - радиус-вектор, проведенный из точки к точке . Получим:

.

Но , так как векторы и коллинеарны. Таким образом, , что и требовалось доказать.

Пусть - ось, неподвижная относительно выбранной инерциальной системы отсчета и проходящая через начало . Обозначим через проекцию вектора на ось . Проекция вектора момента силы на ось называется моментом силы относительно оси.

Для вычисления представим векторы и в виде разложений по двум направлениям - параллельному и нормальному к оси (любой вектор можно разложить по двум любым неколлинеарным направлениям):

.

Получим:

.

Первое слагаемое равно нулю по причине параллельности векторов - сомножителей. Второе и третье слагаемые есть векторы, нормальные соответственно к векторам и , а значит и к оси , их проекции на эту ось равны нулю. Ненулевой вклад в проекцию вектора на ось дает лишь последнее слагаемое:

. (7.2)

Рис. 7.2

Векторы и направлены нормально оси , поэтому их векторное произведение коллинеарно оси . С учетом этого получим:

,

где - угол между векторами и , рис.7.2.

Величина равна расстоянию от оси до линии действия силы и называется плечом силы относительно оси . Итак,

. (7.3)

Последняя формула часто используется при решении задач. Конечно, величина может быть как положительной, так и отрицательной. В частности, при расположении векторов и , показанном на рис.7.2, , как это видно из равенства (7.2).

Пример 7.2. Система частиц с массами находится в однородном поле тяжести с ускорением свободного падения . Радиусы-векторы частиц относительно начала равны . Вычислим момент сил тяжести, действующий на систему:

.

Но , где - масса системы, - радиус-вектор, проведенный из начала к центру масс. Получим:

,

то есть такой момент сил, как если бы сила , действующая на систему, была приложена к ее центру масс. Итак, при вычислении момента сил, действующих на систему в однородном поле тяжести, можно считать, что результирующая сила, действующая на систему, приложена к ее центру масс.