
- •Статистические гипотезы:
- •Вычислим эмпирическое значение критерия:
- •Подсчитать сумму рангов в каждой из групп по отдельности, выполнить проверку ранжирования;
- •Статистические гипотезы:
- •Вычислим эмпирическое значение критерия:
- •Критерий Фридмана
- •Статистические гипотезы:
- •Критерий корреляции Спирмена
- •Статистические гипотезы:
- •Вычислим эмпирическое значение критерия:
- •Критические таблицы
- •Критические точки распределения
- •Критические значения т-критерия Вилкоксона
- •Критические значения корреляции Спирмена
U – критерий Манна-Уитни
Статистические гипотезы:
![]() :
Уровень признака в группе 2 не ниже
уровня признака в группе 1.
:
Уровень признака в группе 2 не ниже
уровня признака в группе 1.
![]() :
Уровень признака в группе 2 ниже уровня
признака в группе 1.
:
Уровень признака в группе 2 ниже уровня
признака в группе 1.
Вычислим эмпирическое значение критерия:
проранжировать все значения испытуемых, как если бы они принадлежали одной выборке, всего должно получиться столько рангов, сколько элементов в двух выборках вместе;
подсчитать сумму рангов в каждой из групп по отдельности, выполнить проверку ранжирования;
определить большую из ранговых сумм
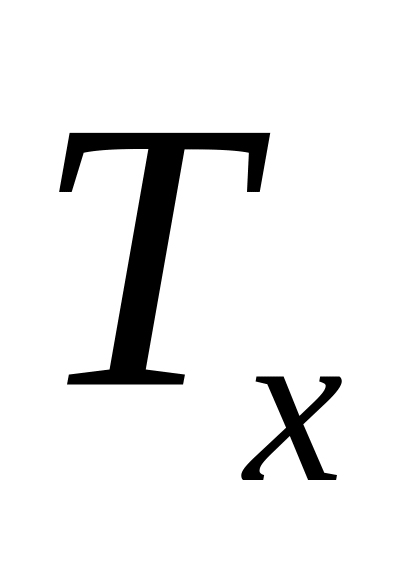 ;
;определить значение
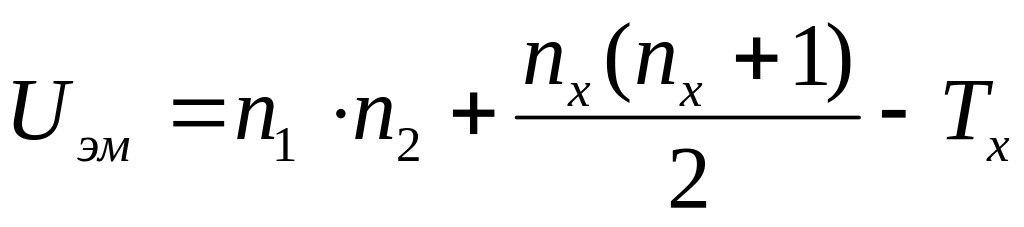 ,
где
,
где
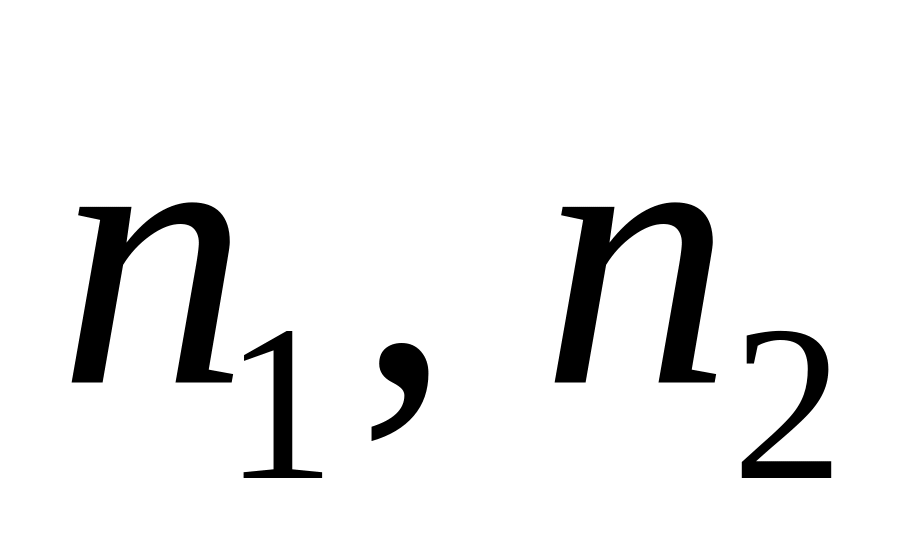 – число испытуемых в выборке 1 и 2
соответственно,
– число испытуемых в выборке 1 и 2
соответственно,
 – количество испытуемых в группе с
большей суммой рангов.
– количество испытуемых в группе с
большей суммой рангов.
По заданному уровню значимости
 и объемам выборок
и объемам выборок
 и
и
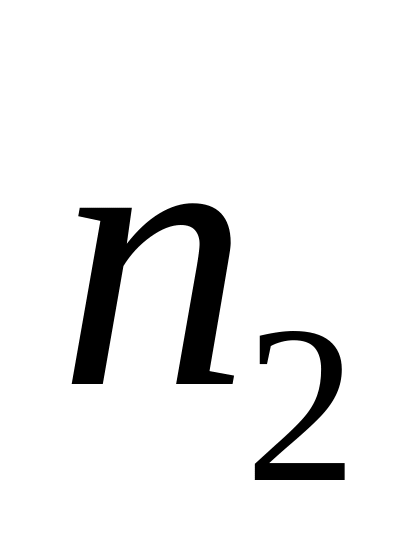 определить критические значения
определить критические значения
 .
.Правило вывода: если
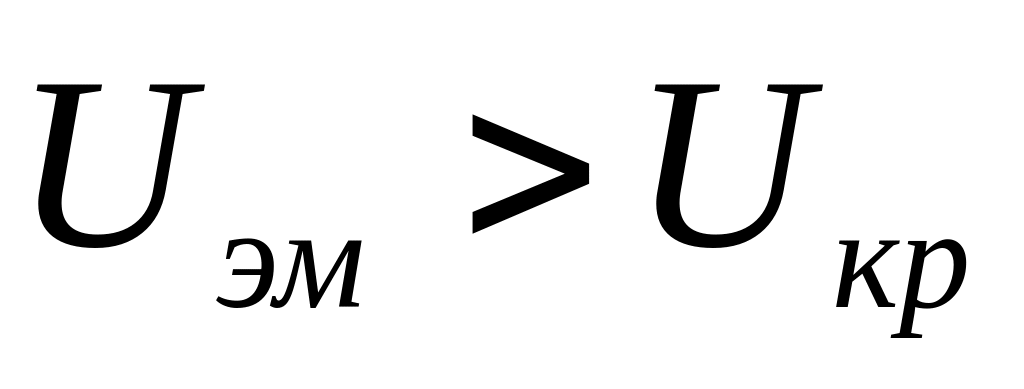 ,
то принимается гипотеза
;
если
,
то принимается гипотеза
;
если
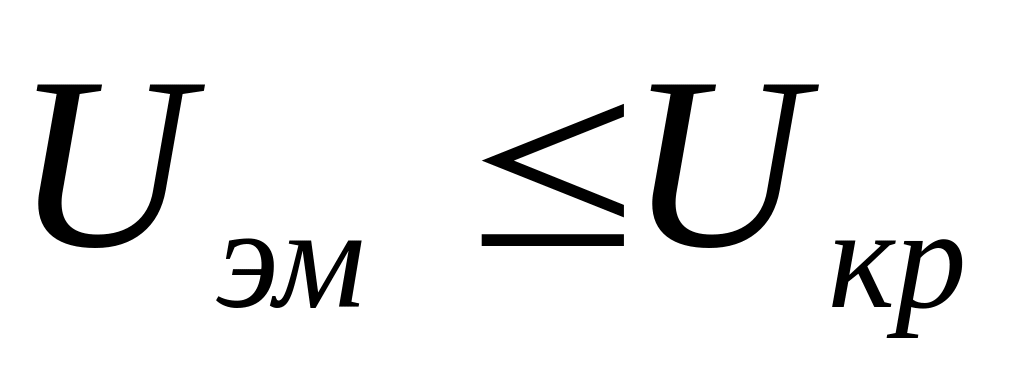 ,
то отвергается гипотеза
.
,
то отвергается гипотеза
.
Пример. Были обследованы студенты физического и психологического факультетов по уровню невербального интеллекта. Можно ли утверждать, что одна из выборок превосходит другую по уровню невербального интеллекта?
Студенты-физики |
Студенты-психологи |
111 |
113 |
104 |
107 |
107 |
123 |
90 |
122 |
115 |
117 |
107 |
112 |
106 |
105 |
107 |
108 |
95 |
111 |
116 |
114 |
127 |
102 |
115 |
104 |
102 |
|
99 |
|
Проранжируем выборки.
Студенты-физики |
Студенты-психологи |
||
90 |
1 |
|
|
95 |
2 |
|
|
99 |
3 |
|
|
102 |
4,5 |
102 |
4,5 |
104 |
6,5 |
104 |
6,5 |
|
|
105 |
8 |
106 |
9 |
|
|
107 |
11,5 |
107 |
11,5 |
107 |
11,5 |
|
|
107 |
11,5 |
|
|
|
|
108 |
14 |
111 |
15,5 |
111 |
15,5 |
|
|
112 |
17 |
|
|
113 |
18 |
|
|
114 |
19 |
115 |
20,5 |
|
|
115 |
20,5 |
|
|
116 |
22 |
|
|
|
|
117 |
23 |
|
|
122 |
24 |
|
|
123 |
25 |
127 |
26 |
|
|
|
165 |
|
186 |
Общая сумма рангов:
![]() .
Расчетная сумма равна
.
Расчетная сумма равна
![]() .
.
Сформулируем гипотезы:
: Уровень признака в группе студентов-физиков не ниже уровня признака в группе студентов-психологов.
: Уровень признака в группе студентов-физиков ниже уровня признака в группе студентов-психологов.
Тогда
![]() ,
,
![]() .
.
Вычислим эмпирическое
значение критерия
![]() .
.
Найдем критическое
значение:
![]() .
.
Так как
![]() ,
то принимается гипотеза
,
то принимается гипотеза
![]() .
Таким образом, группы студентов-физиков
и студентов-психологов можно считать
равными.
.
Таким образом, группы студентов-физиков
и студентов-психологов можно считать
равными.
H – критерий Крускала-Уоллиса
Статистические гипотезы:
![]() :
Между выборками существуют лишь случайные
различия по уровню исследуемого признака.
:
Между выборками существуют лишь случайные
различия по уровню исследуемого признака.
![]() :
Между выборками существуют неслучайные
различия по уровню исследуемого признака.
:
Между выборками существуют неслучайные
различия по уровню исследуемого признака.
Вычислим эмпирическое значение критерия:
проранжировать все значения испытуемых, как если бы они принадлежали одной выборке, всего должно получиться столько рангов, сколько элементов во всех выборках вместе;
Подсчитать сумму рангов в каждой из групп по отдельности, выполнить проверку ранжирования;
Определить значение
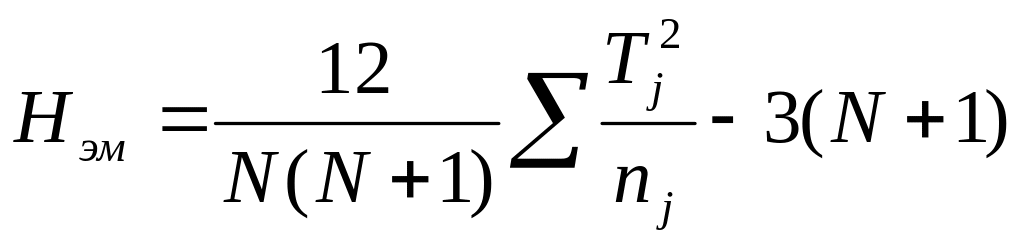 ,
где
,
где
 – общее число испытуемых,
– общее число испытуемых,
 – ранговые суммы в каждой группе,
– ранговые суммы в каждой группе,
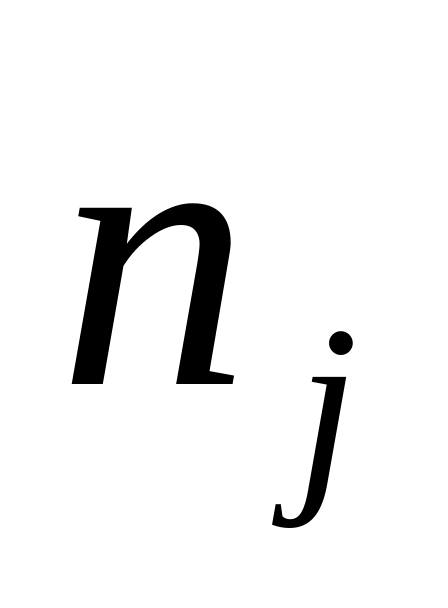 – количество испытуемых в группе.
– количество испытуемых в группе.
По заданному уровню значимости и числу степеней свободы
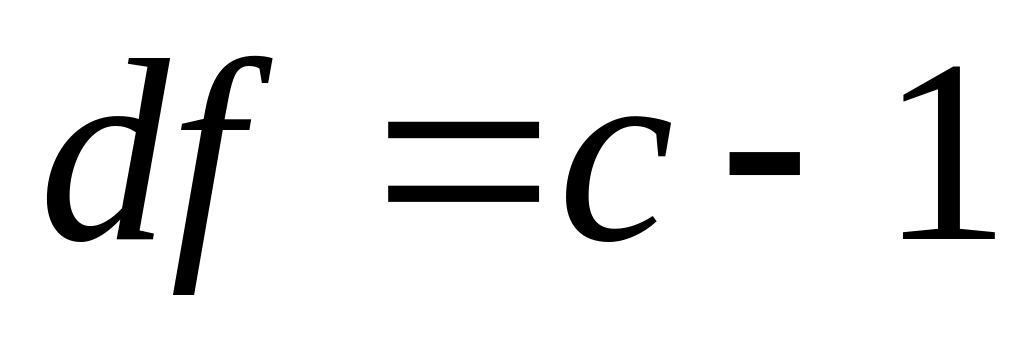 ,
где
,
где
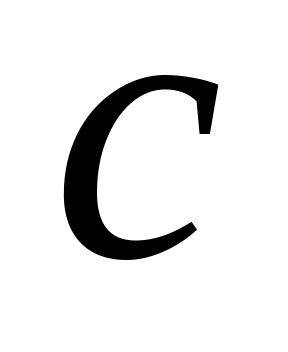 – число отдельных групп, определить
критические значения
– число отдельных групп, определить
критические значения
 .
.Правило вывода: если
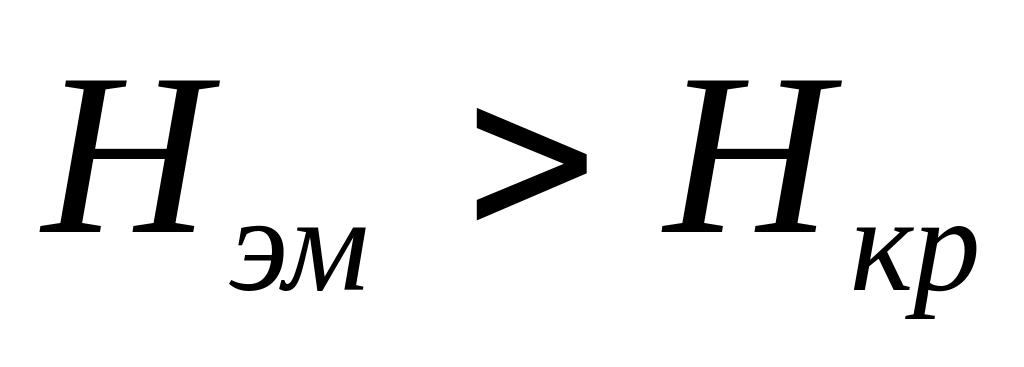 ,
то гипотеза
отвергается; если
,
то гипотеза
отвергается; если
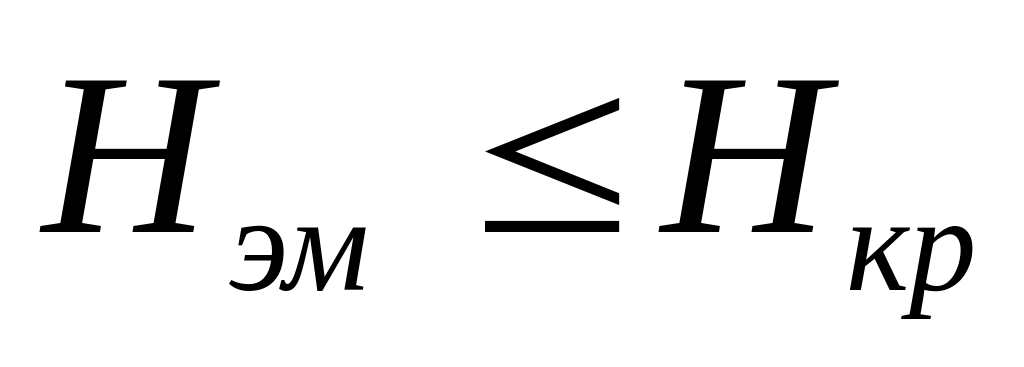 ,
то
принимается.
,
то
принимается.
Пример. При проведении эксперимента по исследованию интеллектуальной настойчивости испытуемым предъявлялись неразрешимые анаграммы. Исследованию подвергались четыре группы испытуемых, каждой группе предъявлялись разные анаграммы. Необходимо проверить, что различие во времени решения анаграмм не связана с предложенной задачей.
№ |
Группа 1 |
Группа 2 |
Группа 3 |
Группа 4 |
1 |
145 |
145 |
128 |
60 |
2 |
194 |
210 |
283 |
2361 |
3 |
731 |
236 |
469 |
2416 |
4 |
1200 |
385 |
482 |
3600 |
5 |
|
720 |
1678 |
|
6 |
|
848 |
2081 |
|
7 |
|
905 |
|
|
8 |
|
1080 |
|
|
Сформулируем гипотезы:
: 4 группы испытуемых не различаются по длительности попыток их разрешения.
: 4 группы испытуемых различаются по длительности попыток их разрешения.
Вычислим эмпирическое значение критерия.
Заполним таблицу для ранжирования
№ |
Группа 1 |
Группа 2 |
Группа 3 |
Группа 4 |
||||
Данные |
Ранг |
Данные |
Ранг |
Данные |
Ранг |
Данные |
Ранг |
|
|
|
|
|
|
|
|
60 |
1 |
|
|
|
|
|
128 |
2 |
|
|
|
145 |
3,5 |
145 |
3,5 |
|
|
|
|
|
194 |
5 |
|
|
|
|
|
|
|
|
|
210 |
6 |
|
|
|
|
|
|
|
236 |
7 |
|
|
|
|
|
|
|
|
|
283 |
8 |
|
|
|
|
|
385 |
9 |
|
|
|
|
|
|
|
|
|
469 |
10 |
|
|
|
|
|
|
|
482 |
11 |
|
|
|
|
|
720 |
12 |
|
|
|
|
|
731 |
13 |
|
|
|
|
|
|
|
|
|
848 |
14 |
|
|
|
|
|
|
|
905 |
15 |
|
|
|
|
|
|
|
1080 |
16 |
|
|
|
|
|
1200 |
17 |
|
|
|
|
|
|
|
|
|
|
|
1678 |
18 |
|
|
|
|
|
|
|
2081 |
19 |
|
|
|
|
|
|
|
|
|
2361 |
20 |
|
|
|
|
|
|
|
2416 |
21 |
|
|
|
|
|
|
|
3600 |
22 |
Сумма |
|
38,5 |
|
82,5 |
|
68 |
|
64 |
Сумма рангов равна
![]() ,
контрольная сумма
,
контрольная сумма
![]() .
.
![]()
![]()
Вычислим критическое
значение
![]() .
.
Поскольку
![]() ,
то принимается нулевая гипотеза. Таким
образом, группы можно считать равными.
,
то принимается нулевая гипотеза. Таким
образом, группы можно считать равными.
T-критерий Вилкоксона
