Вариант 7

1. Найти и изобразить на чертеже область определения функций

а)z = arccos(x + y); б) z = .

2. Вычислить приближенно 0,97 1,05.

3. Найти частные производные и полный дифференциал функции z = arcsin(2x³y).

4. Вычислить значение производной сложной функции u = x^y, где x = e^t ,y = lnt при t = 1, с точностью до двух знаков после запятой.

5. Вычислить значения частных производных функции z = z(x,y), заданной неявно: cos² x + cos²y + cos²z = 1,5 в данной точке M₀ ( ) с точностью до двух знаков после запятой.

6. Проверить, удовлетворяет ли данная функция u = sin²(x-ay) указанному уравнению .

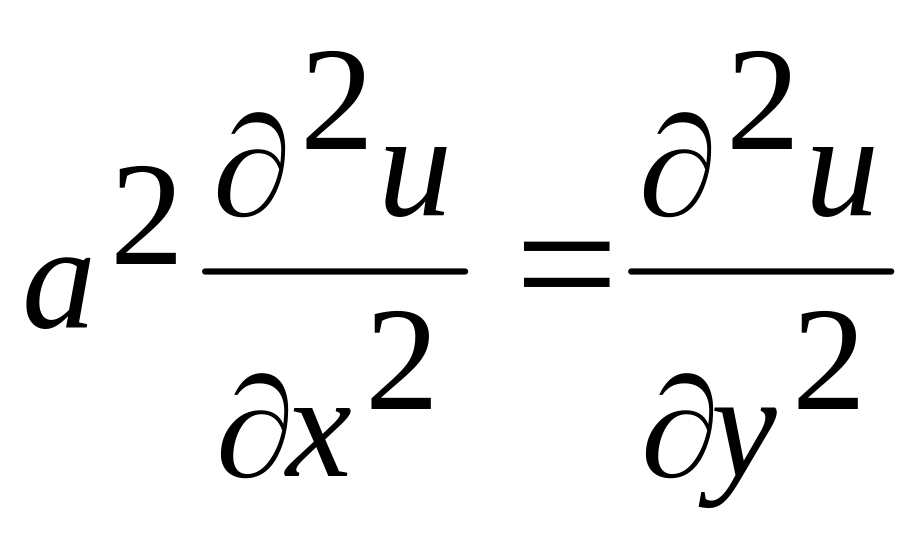7. Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке M₀ (x₀,y₀,z₀). Поверхность, заданную в пункте б), изобразить на чертеже.

а) S: x²+z²-5yz+3y = 46, M₀(1,2,-3);

б) S: 3x²+y² = 9, M₀( ,2 2,1).

8. Определить градиент и производную заданной функции z = xe^y в т. M₀(2,2) в направлении линии xy = 4 в сторону возрастания аргумента x.

9. Исследовать на экстремум функцию z = 3x³+3y³-9xy+10.

10. Найти наибольшее и наименьшее значения функции z = 2x³-xy²+y² в области

D: y = 0,y = 6, x = 0,x = 1.

Вариант 8

1. Найти и изобразить на чертеже область определения функций

а)z = ; б)z = arcsin(3-x²-y²) .

2. Вычислить приближенно .

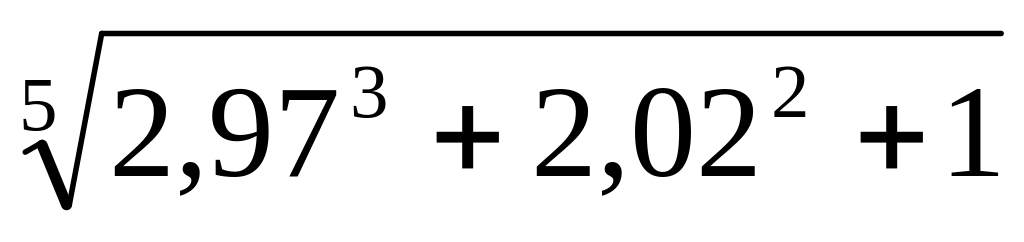3. Найти частные производные и полный дифференциал функции z = ln(3x²y-y²).

4. Вычислить значение производной сложной функции u = e^y-2x, где x = sint, y = t³ при t = 0, с точностью до двух знаков после запятой.

5. Вычислить значения частных производных функции z = z(x,y),заданной неявно: e ^z-1 = cosxcosy + 1, в данной точке M₀ (0,π/2,1) с точностью до двух знаков после запятой.

6. Проверить, удовлетворяет ли данная функция 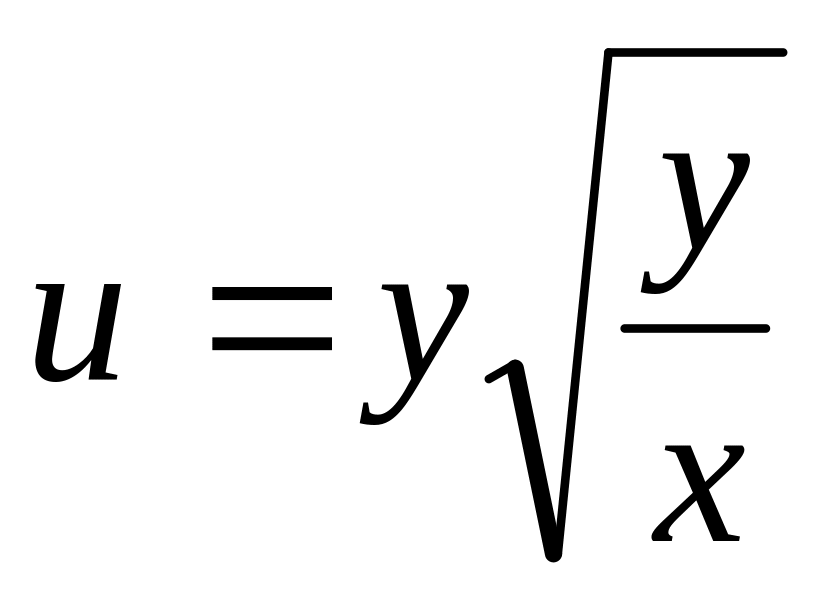указанному уравнению .

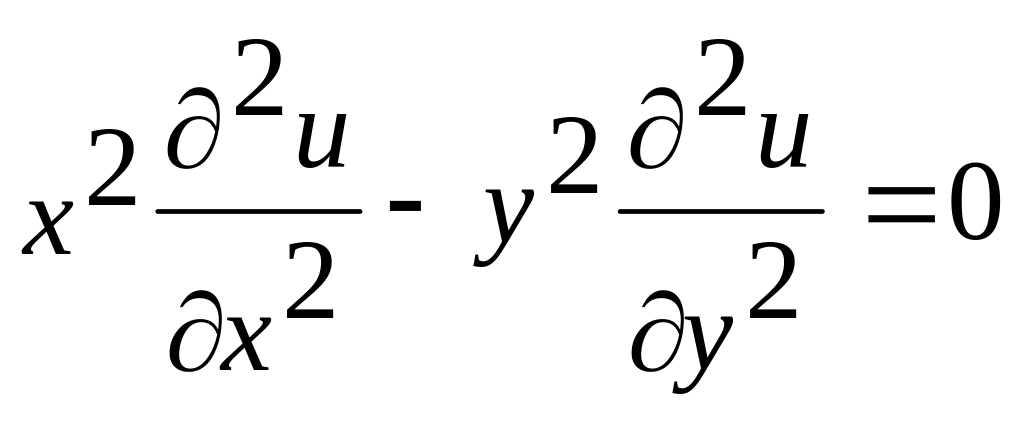7. Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке M₀ (x₀,y₀,z₀). Поверхность, заданную в пункте б), изобразить на чертеже.

а) S: x²+y²-xz-yz = 0, M₀(0,2,2);

б) S: x²+y²-4z² = 4, M₀(-2,2,1).

8. Определить градиент и производную заданной функции z = arcsin( ) в т. M₀(5,5) в направлении линии y² = 5x в сторону возрастания аргумента x.

9. Исследовать на экстремум функцию z = x²+xy+y²+x-y+1.

10. Найти наибольшее и наименьшее значения функции z = 3x+6y-xy-x²-y² в области D: y = 0,y = 1, x = 0,x = 1.

Вариант 9

1. Найти и изобразить на чертеже область определения функций

а)z = ln(x²+y²-3); б) .

2. Вычислить приближенно ln((2,02)²+ ).

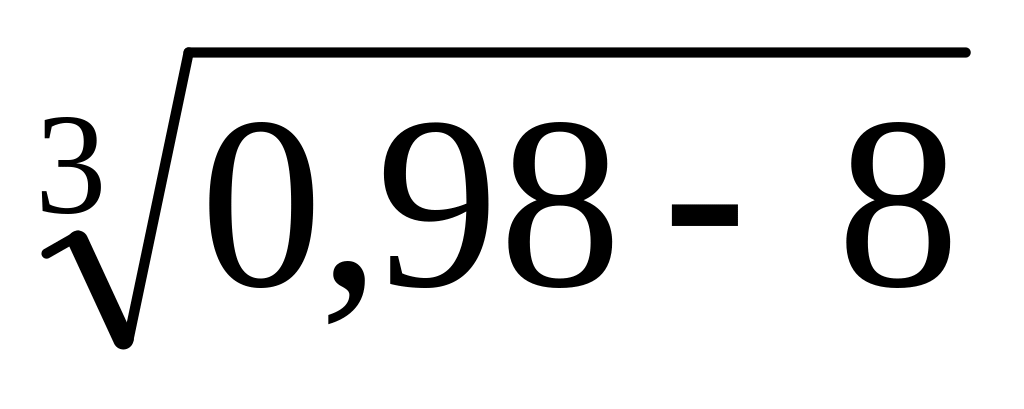3. Найти частные производные и полный дифференциал функции z = e^-(x3+y3)y.

4. Вычислить значение производной сложной функции u = x²e^-y, где x = sint, y = sin²t при t = , с точностью до двух знаков после запятой.

5. Вычислить значения частных производных функции z = z(x,y) , заданной неявно: x²+y²+z²-6x = 0, в данной точке M₀ (1,2,1) с точностью до двух знаков после запятой.

6. Проверить, удовлетворяет ли данная функция указанному уравнению .

7. Найти уравнения касательной плоскости и нормали к заданной поверхности s в точке m0 (x0,y0,z0). Поверхность, заданную в пункте б), изобразить на чертеже.

а) S: x²+y²-z²+2yz+y-2z = 2, M₀(1,1,1);

б) S: x²-y² = 16, M₀(5,3,-1).

8. Определить градиент и производную заданной функции z = ln(x²+y²) в т. M₀(1,1) в направлении линии x²+ y² = 2 в сторону возрастания аргумента x.

9. Исследовать на экстремум функцию z = 4(x-y)-x²-y².

10. Найти наибольшее и наименьшее значения функции z = x²-2y²+4xy-6x-1 в области D: x+y = 3,y = 0, x = 0.