Тема 9. Показатели вариаций. Вариация признака совокупности.

При изучении социально – экономических явлений и процессов, статистика встречается с разнообразной вариацией признаков, характеризующих отдельные единицы совокупности. Величины признаков колеблются, варьируют под действием различных причин и условий, которые в статистике называются факторами.

Среди них есть существенные факторы, которые определяют величину вариантов данного признака у всех единиц совокупности.

Систематическая вариация - вариация, порождаемая существенными факторами, которая носит систематический характер, т.е. наблюдается последовательное соблюдение вариантов признака в определённом направлении.

В систематической вариации проявляются взаимосвязи между явлениями, а также их признаками. В такой связи, один как причина (фактор), а другой – как следствие (результат) его действия, т.е. проявляется зависимость вариации одного признака от вариации другого признака, или от нескольких других признаков.

Общая вариация - вариация зависимого признака, которая образуется под действием всех, без исключения, влияющих на него факторов.

Пример.

Есть два варьирующих (изменяющихся) признака: возраст матерей и доля мальчиков среди детей, родившихся у матерей до 45-летнего возраста.

Доля мальчиков, родившихся у матерей до 45 лет:

Возраст матерей, лет	Моложе 20	20 – 24	25 – 29	30 – 34	35 – 39	40 – 44
На 1000 девочек приходится мальчиков	1057	1054	1051	1046	1044	1035

Из таблицы видно, что от возраста матери зависит доля мальчиков среди новорожденных, т.е. наблюдается системная вариация варьирующего признака.

В процессе анализа необходимо вычислить различные часовые характеристики (показатели), которые в обобщённом виде отражают особенности распределения изучаемых признаков.

Все показатели вариаций, в зависимости от характеризуемых ими особенностей, можно разделить на 3 группы.

ГРУППЫ показателей вариаций:

1. Показатели центра распределения (средняя арифметическая, мода, медиана).

2. Показатели степени вариации (вариационный размах, среднее линейное отклонение, дисперсия, среднеквадратичное отклонение, коэффициент вариации).

3. Показатель типа (формы) распределения (структурные характеристики, показатели ассиметрии и эксцесса, кривые распределения).

Мода и медиана характеризуют величину варианта, занимающего определённое расположение в ранжированном вариационном ряду (от слова «ранг»).

Мода (Мо) распределения – величина изучаемого признака, который в данной совокупности встречается довольно часто, т.е. один из вариантов признака повторяется чаще, чем все остальные.

Пример.

Определить моду (Мо) по не сгруппированным данным.

В рабочей бригаде из 11-ти человек имеют место такие тарифные разряды: 5, 4, 3, 4, 5, 5, 6, 2, 6, 3, 5.

В данной бригаде больше всего рабочих 5-го разряда, и этот тарифный разряд будет модальным.

Для интервального ряда распределения мода Мо

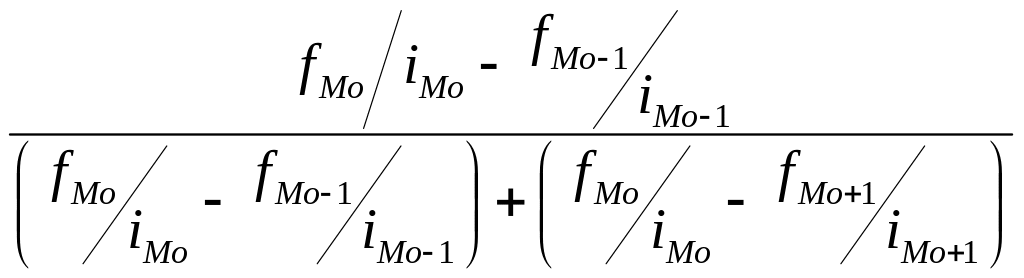Мо = х + i * , где:

х – начальная граница модального интервала, в котором достигает максимума величина f / i – отношение частоты интервала и его величины;

i , i , i - величина соответствующего модального, до-модального и после-модального интервалов;

f , f , f - частота модального, до-модального и после-модального интервалов соответственно.

Распределение коммерческих банков по сроку функционирования:

Группы банков по сроку функционирования, лет,(Х)	Число банков, % к итогу, (f)	Накопленная частота (S)
А	1	2
1 – 2	10	10
2 – 3	15	25
3 – 4	21	46
4 – 5	25	71
5 – 6	12	83
6 – 7	7	90
7 – 8	5	95
Свыше 8	5	100
Итого	100

Мо = х + i *

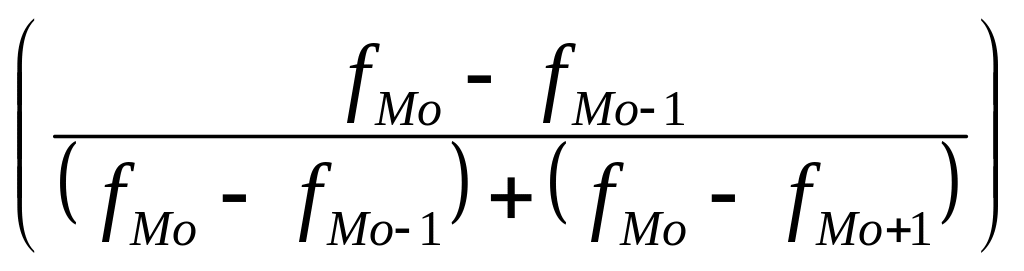
Мо = 4 + 1 * = 4 + 1 * = 4,2

В данной совокупности банков самым распространённым сроком функционирования банка является 4,2 года.

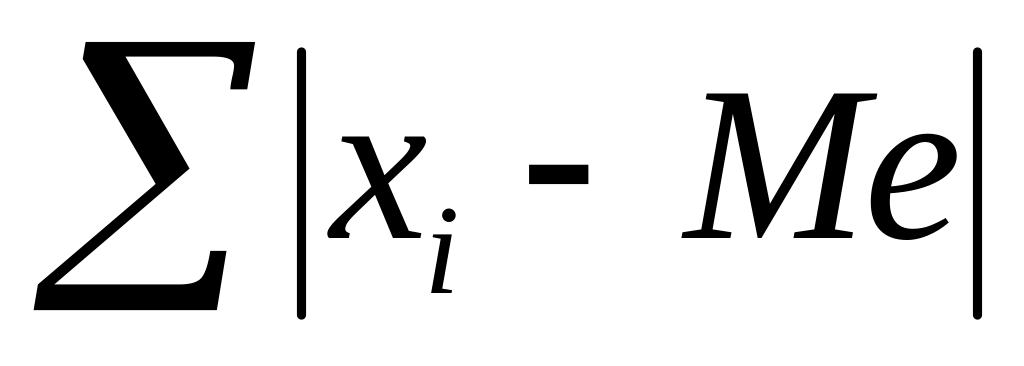1. = min;

2. Ме = min; Ме = x ;

3. Ме = ;

4. № Ме = ;

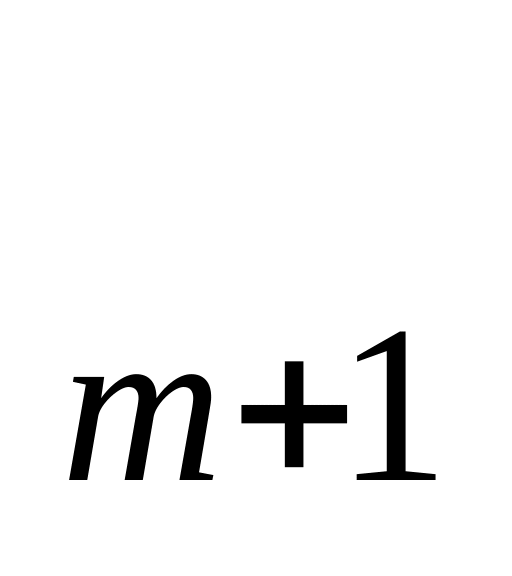5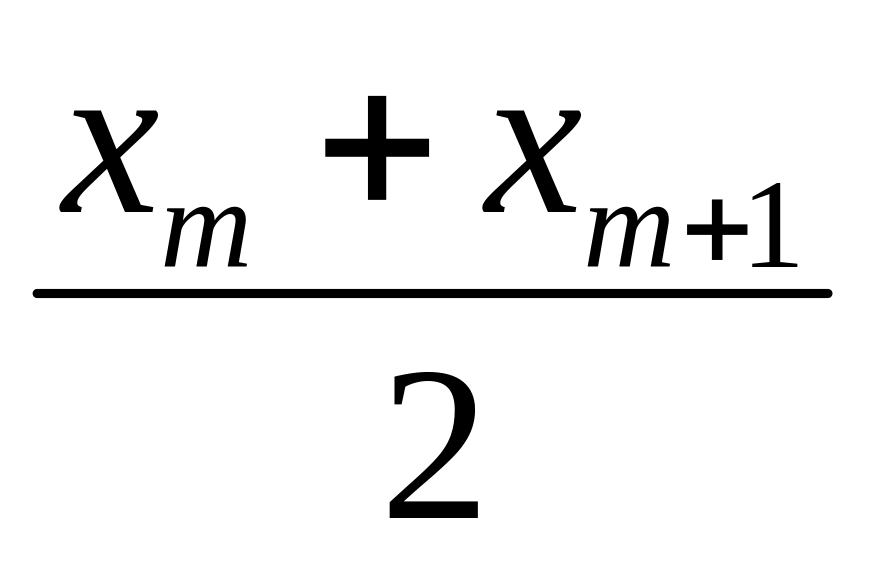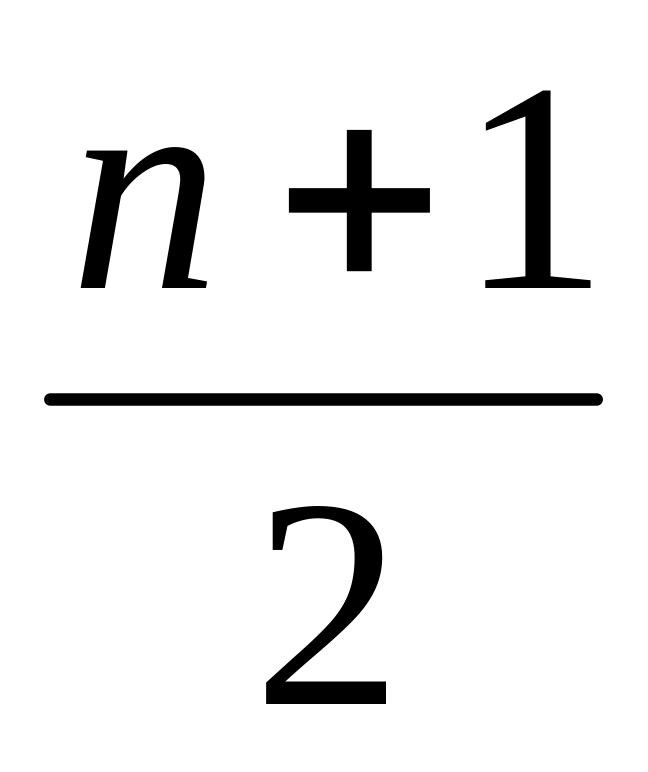. Ме = х +i *

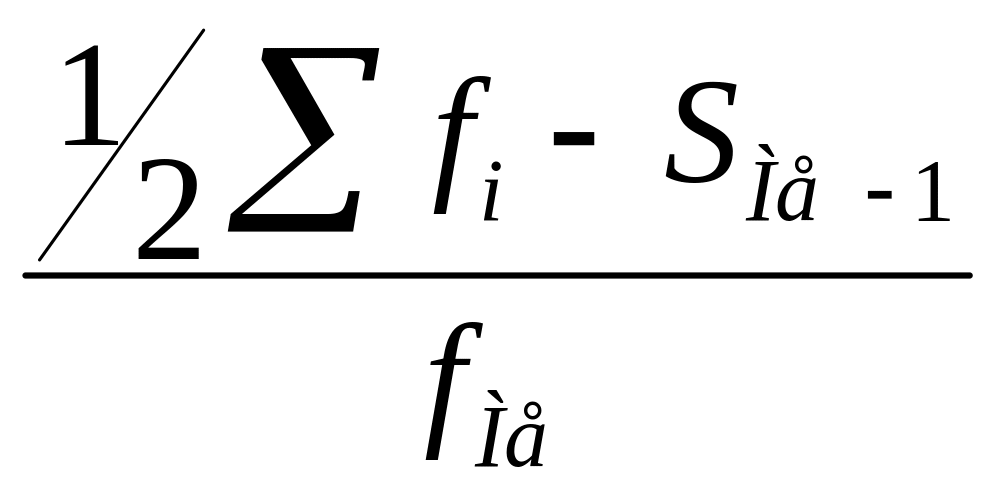
f - частота медианного интервала;

f - накопленная частота интервала, предшествующего медианному.

По задаче: В данной совокупности банков самым распространённым сроком функционирования банка является 4,2 года.

Для характеристики вариационного ряда также применяется медиана – Ме, т.е. величина изучаемого признака, который находится в середине упорядоченного вариационного ряда.

Главное свойство медианы состоит в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой друой величины.

= min (1)

Если в вариационном ряду 2m+1 случаев, то значение признака у случая m+1 будет медианой.

Если в ряду чётное число 2m случаев, то медиана равна средней арифметической из 2-х данных значений.

ФОРМУЛА для вычисления медианы при НЕЧЁТНОМ числе вариантов:

Ме = х (2)

ФОРМУЛА для вычисления медианы при ЧЁТНОМ числе вариантов:

Ме = (3)

Пример.

Определить медиану по данным вариационного ряда из 11-ти рабочих (нечётный ряд), имеющих следующие тарифные разряды: 5, 4, 3, 4, 5, 5, 6, 2, 6, 3, 5.

Решение.

Для определения медианы проведём ранжирование ряда по тарифному разряду: 2 – 3 – 3 – 4 – 4 – 5 – 5 – 5 – 5 – 6 – 6.

Центральным в этом ряду будет рабочий 5-го разряда, поэтому данный разряд будет медианным.

Если ранжированный ряд включает в себя 12 рабочих, то получим следующее: 2 – 3 – 3 – 3 – 4 – 4 – 5 – 5 – 5 – 5 – 6 – 6. В данном случае медиана определяется как среднее арифметическое из 2-х центральных значений: 4, 5 .

Мода отражает типичный, наиболее распространённый вариант значения признака. Медиана же практически выполняет функцию средней величины для неоднородной совокупности, не подчиняющейся нормальному закону распределения.

Пример.

Дать характеристику среднего дохода группы людей из 100 человек, 99 из которых имеют доходы в интервале от 100 до 200$ в месяц, а месячный доход последнего человека из группы составляет 50 000$.

Распределение рабочих по тарифному разряду:

№п/п	1	2	3	4…	50	51	…	99	100
Доход ($)	100	104	104	107…	162	164	…	200	50 000

Средний доход составляет 600$ (но он не соответствует действительности).

Если мы воспользуемся формулой среднего арифметического, то получим средний доход ≈ 600 – 700$, который не имеет ничего общего с доходами группы людей из 99-ти человек, а также ниже дохода 100-го человека.

В данном случае медиана позволит дать объективную характеристику уровня доходов 99% данной группы людей.

Ме = 163$ - средняя заработная плата.13.02соц.раб

Используя данные таблицы «Распределение рабочих по тарифному разряду», определим медиану по сгруппированным данным. Для этого определим положение медианы в ряду распределения, который определяется её номером:

№ Ме = (4)

№ Ме = = 108, где n – число единиц в совокупности.

Это значение указывает, что середина ряда приходится на 108-ой номер рабочего.

Необходимо определить, к какой группе относится рабочий с этим порядковым номером. Это можно сделать, рассчитав накопленные частоты, и определить, что 108-й номер рабочего находится в группе (20 + 50 + 60) = 130, т.е. медианным является 4-й тарифный разряд.

Пример.

Используя таблицу «Распределение коммерческих банков по сроку функционирования», рассчитать медиану.

Решение.

По данным таблицы, в интервальном ряду распределения можно указать только интервал, в котором будет находиться медиана.

Для определения её величины использует специальную формулу:

Ме = х + i * (5) Me = x₀ + i*(1\2 f_i – S_Me-1) \ f_Me

Ме = 4 + 1 * 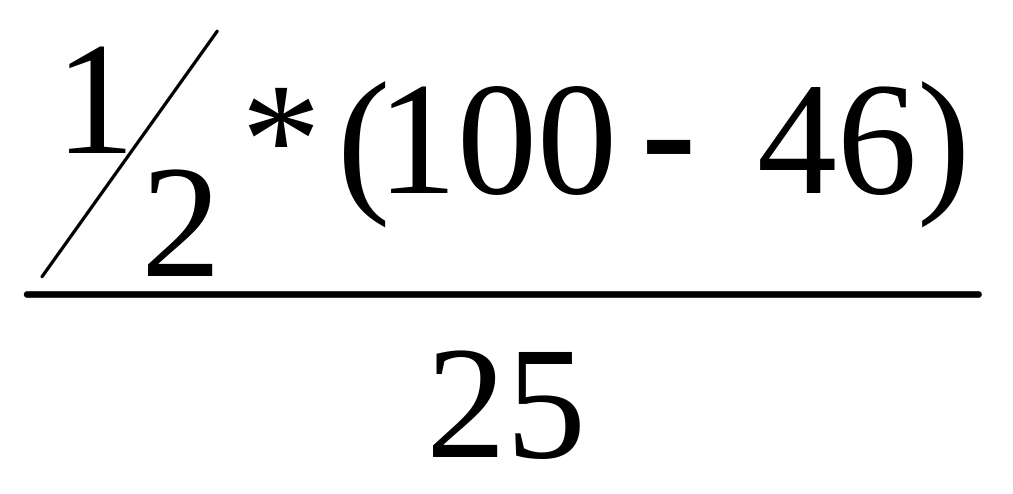= 4,2

f - частота медианного интервала.

f = 100 / 2 = 50.

50% банков имеют срок функционирования менее 4,2 года, а остальные 50% банков – более 4,2 года.

Моду и медиану в интервальном ряду распределения можно определить графически.

Мода определяется по гистограмме. Для этого выбирается самый высокий прямоугольник, который в данном случае является модальным.

График соответствует таблице «Распределение коммерческих банков по сроку функционирования»:

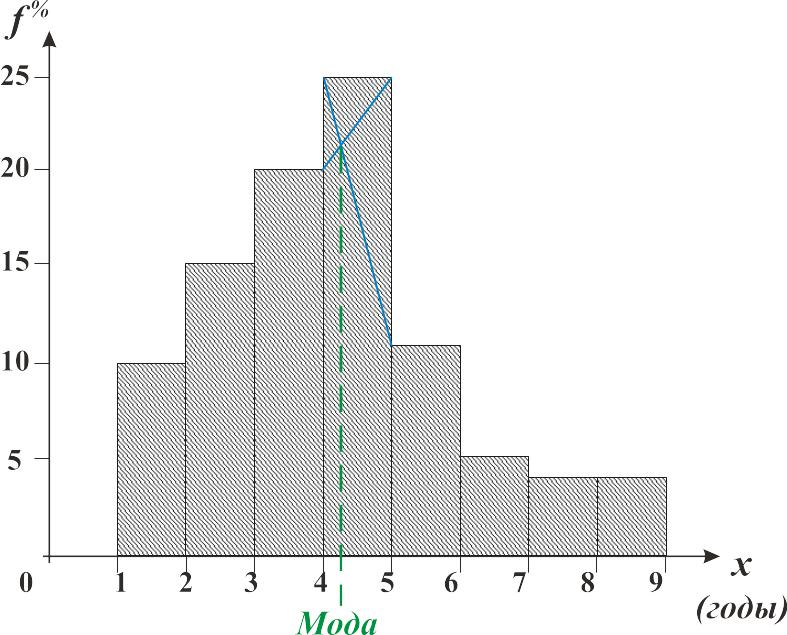
Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника соединяем с левым верхним углом последующего прямоугольника. Из точки их пересечения опускают перпендикуляр на ось абсцисс, и точка пересечения этих прямых на оси абсцисс и будет являться модой распределения.

Медиана рассчитывается по кумуляте.

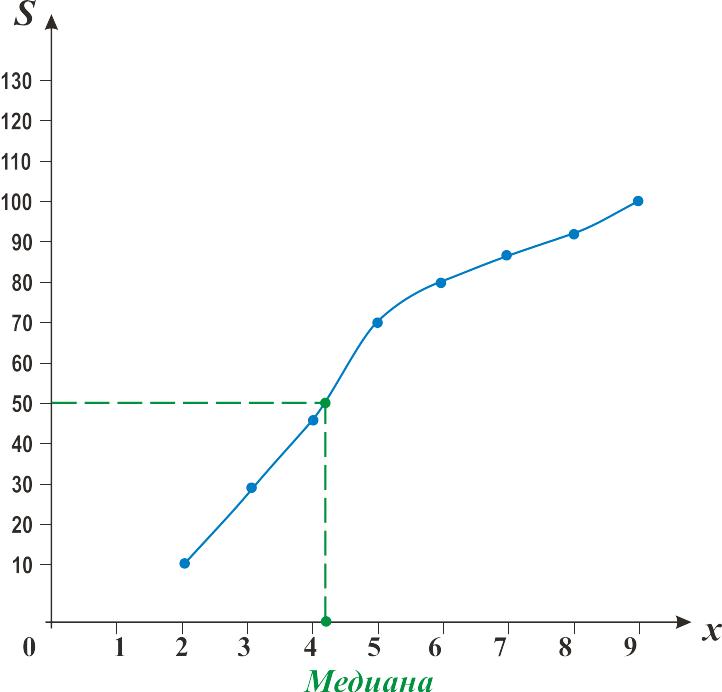
Решение.

Применяем среднегармоническую взвешенную:

=

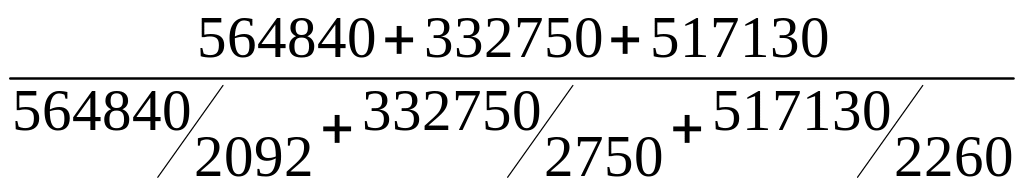= = = = 2282

Ответ: 2282.