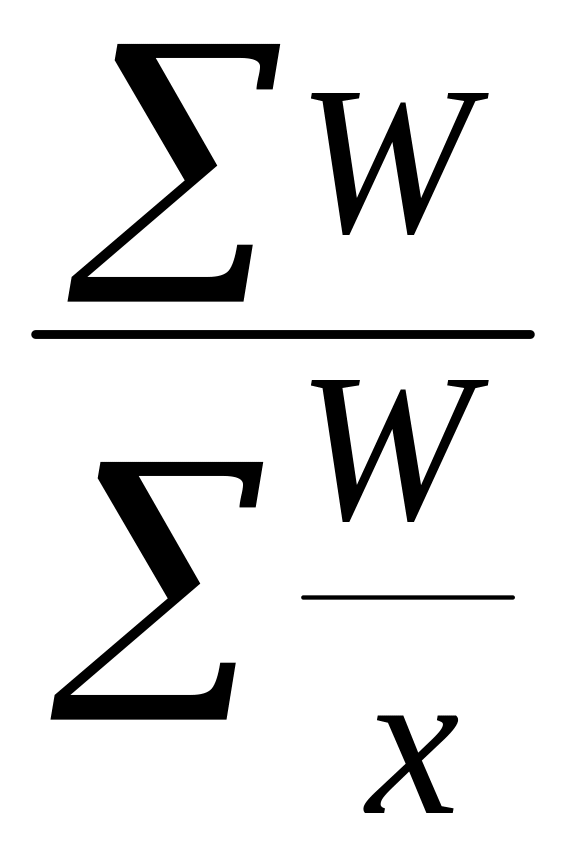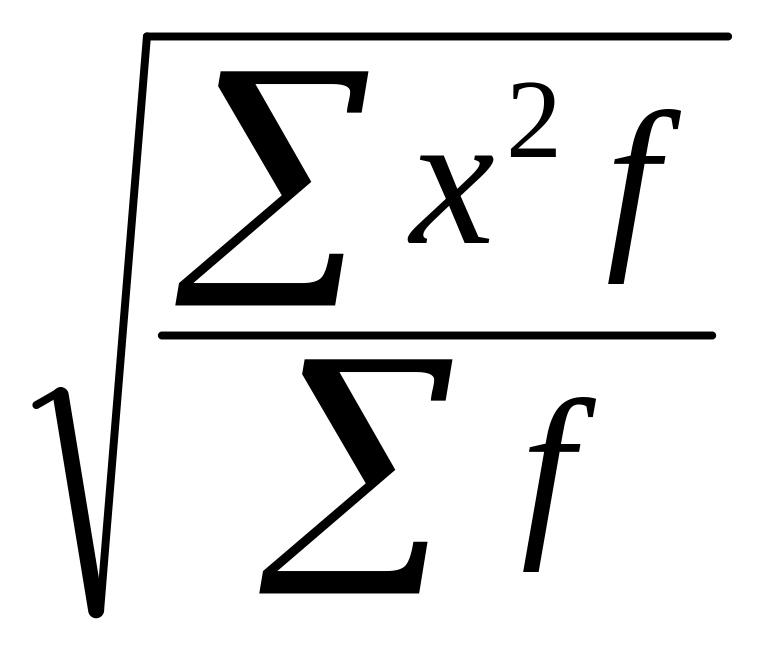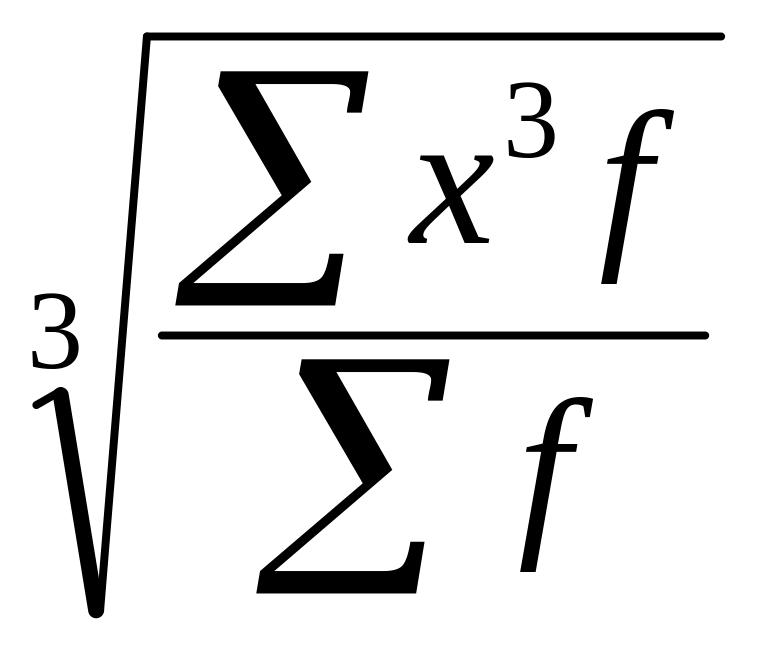Тема 8. Сущность и значение средних показателей.
Средняя величина – обобщённая количественная характеристика признака статистической совокупности в конкретных условиях места и времени.
ВАЖНЕЙШЕЕ СВОЙСТВО средней величины: данная величина отражает то общее, что присуще всем единицам исследуемой совокупности.
Средняя величина только тогда отражает типичный уровень признака, когда она рассчитана по качественно однородной совокупности.
В каждом конкретном случае для реализации исходного соотношения потребуется одна из следующих форм средней величины:
среднее арифметическое;
среднее гармоническое;
среднее геометрическое;
среднее квадратичное;
среднее кубическое.
Величины средних. Методика расчёта – таблица.
Среднее арифметическое – «простая» - используется в тех случаях, когда расчёт осуществляется по не сгруппированным данным.
Например, 7 членов бригады имеют следующий стаж работы:
№ рабочего |
Стаж работы |
1 |
10 |
2 |
3 |
3 |
5 |
4 |
12 |
5 |
11 |
6 |
7 |
7 |
9 |
Средний стаж работы = Совокупный стаж работы всех рабочих / Число рабочих |
|
Средний стаж работы = 57 / 7 = 8,1 (год) |
|
Среднее арифметическое взвешенное – применяется при расчёте средней величины. когда отдельные значения осредняемого признака могут повторяться по несколько раз. В этом случае расчёт проводится по сгруппированным данным или вариационным рядам (дискретным или интервальным).
Продажи акций АО «Дока хлеб»
Сделка |
Количество проданных акций, штук |
Курс продаж, грн. |
1 |
500 |
1080 |
2 |
300 |
1050 |
3 |
1100 |
1045 |
Средний курс = Общая сумма сделок / Количество проданных акций |
||
Средний курс = (500*1080 + 300*1050 + 1100*1045) / 1900 = 1055 |
||
Вид средней величины |
Методика вычисления |
Среднеарифметическая простая |
|
Среднеарифметическая взвешенная |
=
|
Среднегармоническая простая |
=
|
Среднегармоническая взвешенная |
=
|
Среднегеометрическая |
=
|
Среднеквадратичная простая |
=
|
Среднеквадратичная взвешенная |
=
|
Среднекубическая простая |
=
|
Среднекубическая взвешенная |
=
|
=
Где:
=
=
- среднее значение признака;
x – варианта;
f – частота;
п – количество вариант;
Пх – вариант;
- сумма частот;
W – объём явлений.
Задача.
Распределение работников предприятия по возрасту.
Возраст, лет |
Число работников |
до 25 |
7 |
25 – 30 |
13 |
30 – 40 |
38 |
40 – 50 |
42 |
50 – 60 |
16 |
60 и более |
5 |
|
121 |
Определить: средний возраст работников.
Решение.
Находим середины возрастных интервалов: если 25 и 30, шаг – 5, то:
I середина интервала – 22,5;
II середина интервала – 27,5;
III середина интервала – 35;
IV середина интервала – 45;
V середина интервала – 55;
VI середина интервала – 65.
хср.
=
хср.
=
=
= 40,8.
Ответ: 40,8 ≈ 41.
Среднеарифметическая взвешенная.
Рассмотрим вариант, когда известен числитель исходного соотношения средней величины, но не известен его знаменатель.
Область |
Валовый сбор, тыс.т. |
Урожайность, ц/га |
Одесская |
1088,3 |
10,9 |
Николаевская |
601,5 |
12,1 |
Херсонская |
1171,5 |
17,5 |
Днепропетровская |
1050,7 |
8,8 |
Определить: среднюю урожайность.
Решение.
Площадь – S.
1т. = 10ц.
1088,3 тыс. т. = 10 883 000; 1088,3 = 10 883
S = Валовый сбор / Урожайность
S
=
= 11,6 (ц/га).
Ответ: 11,6 (ц/га).
Домашнее задание.
Задача №1.
К какому виду по степени охвата единиц совокупности относится показатель «активы коммерческого банка»:
индивидуальный (верный ответ);
сводный.
Задача №2.
К какому виду по временному фактору относится показатель «число рекламаций на продукцию предприятия»:
моментный;
интервальный (верный ответ).
Задача №3.
Относительный показатель реализации предприятием плана производства продукции составил 103%. При этом объём производства, по сравнению с предшествующим периодом, вырос на 2%. Какой из приведенных вариантов предусматривал план:
снижение объёма производства;
рост объёма производства (верный ответ).
Задача №4.
Описать свойства среднего арифметического.