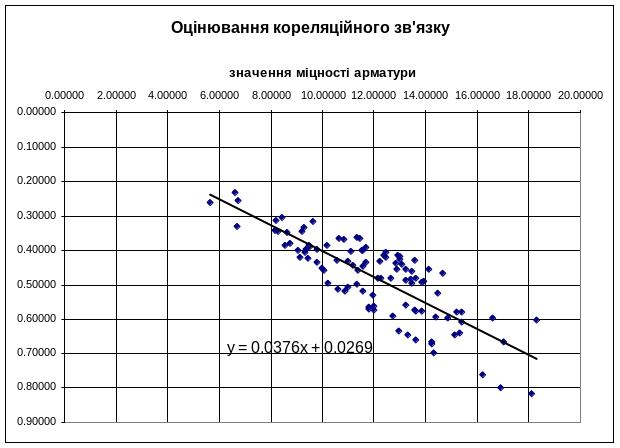
3. Оцінювання кореляційного зв’язку між
значеннями міцності арматури та значеннями ширини розкриття тріщини у залізобетонному елементі крокв’яної конструкції
§3.1. Формула оцінювання зв’язку між вибірками випадкових величин
Силу
кореляційного звязку оцінюємо за
коефіцієнтом кореляції
:
,
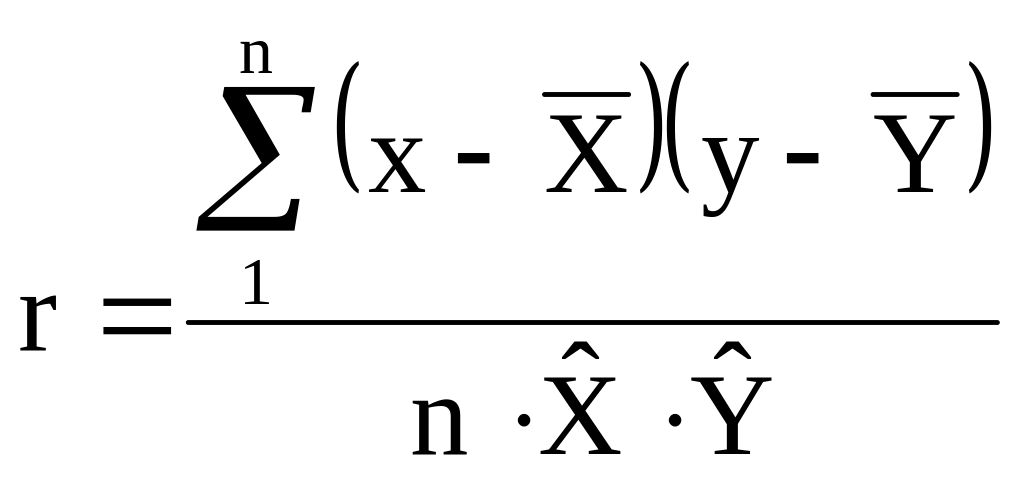де n – кількість випадкових величин у статистичній вибірці,
,
– мат очікування та стандарт міцності
для розглянутих сотні зразків,
,
–
мат очікування та стандарт ширини
розкриття тріщини.
§3.2. Практичне оцінювання кореляції
Наведемо фрагмент автоматизації оцінювання кореляції між міцністю арматури та шириної розкриття тріщини у програмі MSExcel:
За умови отриманого значення коефіцієнта кореляції 0.81228768 > 0.7, можемо зробити висновок про існування посереднього зв’язку між зазначеними статистичних вибірок випадкових величин міцності арматури та ширини розкриття тріщини.
§3.3. Визначення параметрів рівняння регресії та побудова його графіку
Рівняння регресії записується у вигляді лінійної функції:
,
де a та b - є шуканими параметрами цього рівняння.
Параметри рівняння регресії визначаються як:
,
,
=0.0269
Наведемо графік рівняння регресії для заданих випадкових величин
