§1.4. Дібрання теоретичного закону розподілу Гауса та побудова відповідної апроксимуючої кривої нормального розподілу

Задача статистичного оцінювання полягає у тому, щоб на базі результатів повторних вимірювань знайти такі вибіркові характеристики, так звані статистики, за допомогою якихможна було б дати найбільш точну і надійну оцінку відповідним закону і параметрам генеральної сукупності випадкової величини міцності будівельного матеріалу. Тому для розв’язування ріних інженерних задач, зокрема задачі нормування міцності необхідно мати функцію статистичного закону розподілу. Для опису розподілу ймовірностей величин міцності описаного буд матеріалу покажемо таку статистичну функцію на основі розподілу Гауса.

Функція щільності розподілу випадкових величин (ВВ) за законом розподілу Гаусса описується як:

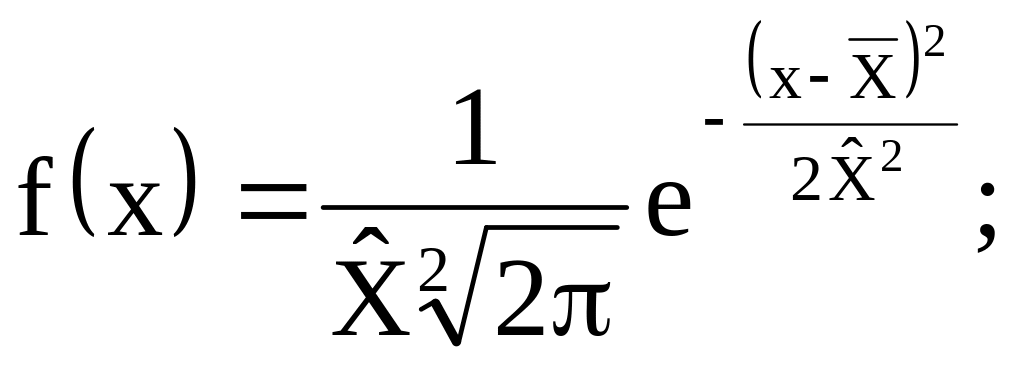
Ординати нормальної кривої для нормованого аргументу при :

Нормований аргумент нормального розподілу визначаємо як:

.

Інтегральна (кумулятивна) функція за цим законом визначається як відповідний інтеграл:

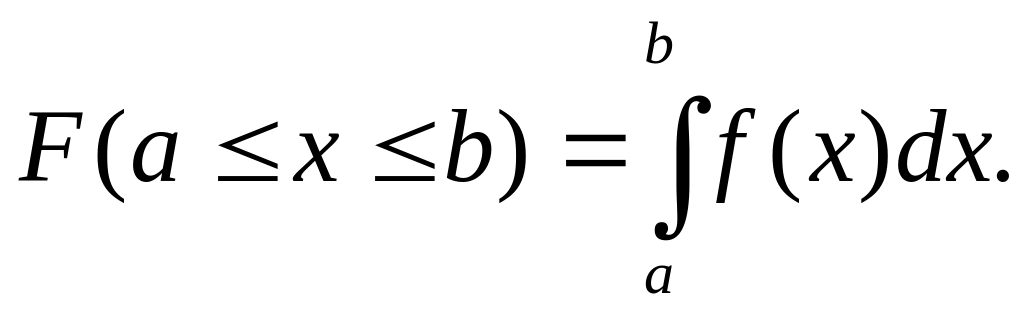
Ця функція характеризує ймовірність попадання випадкової величини у інтервал [a,b]. Для задачі визначення нормативної міцності будівельного матеріалу необхідно мати значення рівня забезпеченості p, яке й буде визначатись відповідним інтегралом:

,

що свідчить про ймовірність такого значення міцності яке буде у інтервалі від нормативного до нескінченно великого із ймовірністю p. Таким чином, відповідним інтегруванням функції щільності можна визначити ймовірності, котрі дорівнюють забезпеченості міцності p. Як відомо, для будівельних конструкцій за значення рівня забезпеченості приймається 0.95, отже:

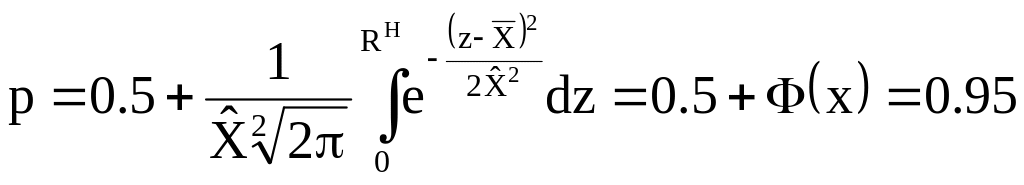
Із цього зрозуміло, що треба мати таблиці функції Лапласа , а самі значення якої визначаються як: .

1.5. Побудова графіків теоретичних кривих диференціальної та кумулятивної функцій

2.Нормування міцності будівельного матеріалу

Нормативне значення міцності будівельних матеріалів нерозривно пов’язане із поняттям забезпеченості р. Інженерна задача нормування міцності будівельних матеріалів полягає у визначенні такого значення цієї міцності, яке відповідає заданому рівню забезпеченості р. Забезпеченість міцності – це ймовірність появи такого значення міцності (при випробовуванні зразка буд. матеріалу), яка за значенням буде не менша за нормативне начення. Так, наприклад, для р=0,95, відповідно, 95% - це ймовірність того, що навмання взятий зразок у межах розглянутої партії будівельного матеріалу буде мати міцність не меншу за нормативне значення.

Наведемо схеми графіків описаних функцій (щільності та кумулятивної), на основі яких проводять нормування характеристик міцності будівельних матеріалів, якщо розподіл міцності підпорядковується саме закону Гаусса:

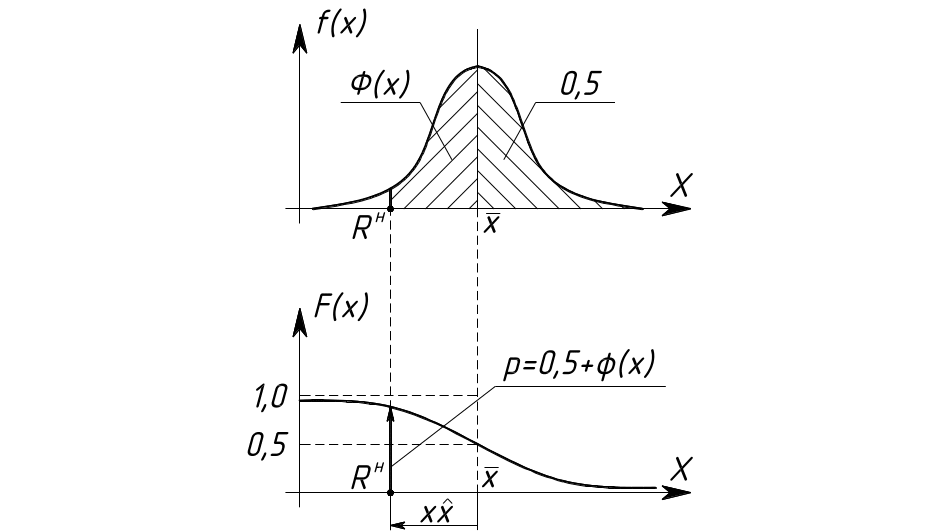
Враховуючи симетричний розподіл функції Гаусса, функцію ймовірності зручно визначати за функцією Лапласа , яка визначається як інтегральна за умови границь інтеграла [0,z]:

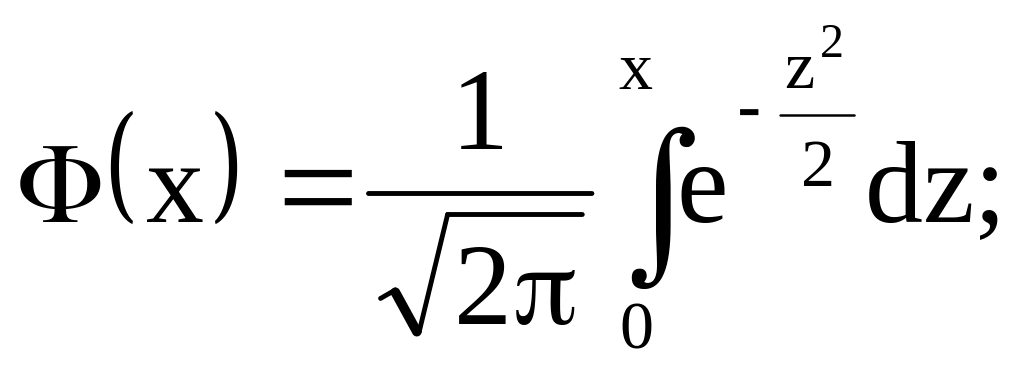
Ймовірність потрапляння випадкового значення міцності у інтервал дорівнює 0.5, тому необхідно визначити значення функції Лапласа та додати до нього 0.5, - це й буде ймовірність потрапляння ВВ міцності у диапазон , що зумовлює значення забезпеченості р:

.

Визначення нормативної міцності проведемо для загально прийнятої у будівництві забезпеченості рівної p=0.95.